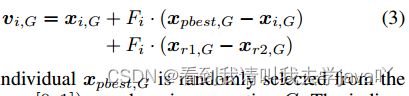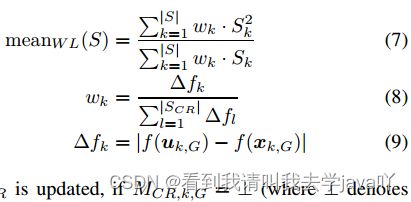L-SHADE（Improving the Search Performance of SHADE Using Linear Population Size Reduction）

Abstract

L-SHADE在SHADE的基础上，扩展了线性种群规模缩减（LPSR），即根据线性函数不断减少种群规模。

II SUCCESS-HISTORY BASED ADAPTIVE DE WITH

DE表示为实参向量$x_i=(x_1,\dots \dots ,X_D),i=1,\dots \dots ,N$，$D$为维度，$N$是种群数。搜索开始时，种群中的向量初始化，重复策略直至终值。

A. Control parameters assignments based on historical memory

SHADE控制DE的参数$CR$、$F$、$M_{CR}$和$M_F$。缩放因子$F\in [0,1]$控制差分突变因子，$CR\in [0,1]$是交叉率，开始时$M_{CR,k}$和$M_{F,k}(k=1,\dots \dots ,H)$被初始化为0.5，通过从$[1,H]$随机选择一个下标$r_i$，生成每个个体的参数：

如果交叉率$C{R}_i$生成了[0,1]之外的值，则生成最近的$0$或$1$。
当$F_i>1$时，$F_i$被截断为$1$；当$F_i\le 0$，重复$(2)$式，以生成有效值。
以上为JADE。

B. Reproduction of trial vectors by using current-topbest/1/bin

在为每个个体$x_{i,G}$分配了$C{R}_i$和$F_i$后，通过应用current-to-pbest/1突变策略（即JADE使用的突变策略）和current-to-best/1 策略，生成突变向量，其中贪婪度可以使用$p$来调整：

其中，个体$x_{pbest,G}$是第$G$次迭代的前$N\times p(p\in [0,1])$中随机挑选的，$r_1$和$r_2$是从$[1,N]$中随机挑选的，彼此不同。current-to-pbest/1的贪婪程度取决于控制参数$p$，小$p$更加贪婪。
针对每个维度$j$，若突变向量$x_{j,i,G}$在边界$[x_j^{min},x_j^{max}]$之外，则应校正：

在生成突变向量$v_{i,G}$后，将其与父向量$x_{i,G}$交叉，生成试验向量$u_{i,G}$，使用如下交叉策略Binomial Crossover：

C. Survival for next generation

选择策略，保留更好的：

D. External archive

在JADE中，外部存档external archive用于维护多样性。
比$u_{i,G}$差且未被公式$(6)$选择的$x_{i,G}$保存下来。
当使用存档时，式$(3)$中的$x_{r_2,G}$是从集合$P\bigcup A$中选取的，其中$P$是种群，$A$是存档库。
每当存档的大小超过预定的存档大小$|A|$时，则随机删除元素再插入新元素。

E. Historical-memory update

在每一次迭代中，经过选择后生成$u_{i,G}$的$C{R}_i$和$F_i$要比生成$x_{i,G}$的$S_{CR}$和$S_F$更好，因此更新，此步算法如下：

其中，索引$k（1\le k\le H）$决定了更新在内存中的位置。$k$初始化为$1$，每当有新的元素插入时，$k$增加，在第$G$次迭代中，内存中第$k$个元素会被更新。当$k>H$时，$k=1$。
当所有个体都不能生成优于$x$的$u$时，不更新。

加权Lehmer均值$mea{n}_{WL}(S)$由下式计算，适应度改善量$△f_k$用于影响参数自适应（$S$指$S_{CR}$或$S_F$）

如果$M_{CR,k,G}=\perp$或$max(S_{CR})=0$（例如$S_{CR}$的所有元素都为$0$），$M_{CR,k,G+1}=\perp$。因此如果$M_{CR}=\perp$，则保持此值直至结束，即$CR$一直保持为$0$，这将会减慢收敛速度，对多模态问题有效。

F. Linear Population Size Reduction (LPSR) and L-SHADE algorithm

本文使用线性种群规模缩减（LPSR），即SVPS的简单特化，作为适应度评估函数线性地缩减种群规模。
LPSR不断缩减种群以匹配一个线性函数。在第一次迭代时，种群规模数是$N^{init}$，运行结束时种群规模数是$N^{min}$。在每一次迭代后，下一次迭代的种群规模按如下公式计算：

其中，$N^{min}$被设置为可能的最小值。在L-SHADE中，$N^{min}=4$，因为current-to-pbest突变策略需要$4$个个体。
$NFE$是当前适应度评价的个数，$MAXNFE$是适应度评价的最大个数。
当$N_{G+1}<N_G$时，$(N_G-N_{G+1})$个排名最差的个体从种群中删除。

在上图算法中，行21-24加入了LPSR，在行24中，参数$|A|$被重新调整，性能优于$|A|=N^{init}$。