【算法实验】实验3
实验3-1 快速排序
#include
using namespace std;
void Quicksort(int arry[],int L,int R)
{
if(L>=R) return ;
int left=L,right=R;
int pivot=arry[left];
while(left=pivot)
right--;
if(left=right) arry[left]=pivot;
}
Quicksort(arry,L,right-1);
Quicksort(arry,right+1,R);
}
int main()
{
int ans[5]={2,5,3,6,1};
Quicksort(ans,0,4);
for(int i=0;i<5;i++)
cout< 实验3-2 众数问题
问题描述:
给定含有n 个元素的多重集合S,每个元素在S 中出现的次数称为该元素的重数。多重集S 中重数最大的元素称为众数。
例如,S={1,2,2,2,3,5}。
多重集S 的众数是2,其重数为3。
编程任务:
对于给定的由n 个自然数组成的多重集S,编程计算S 的众数及其重数。
数据输入:
输入数据由文件名为input.txt 的文本文件提供。文件的第1 行多重集S 中元素个数n;接下来的n 行中,每行有一个自然数。
结果输出:
程序运行结束时,将计算结果输出到文件output.txt 中。输出文件有2 行,第1 行给出众数,第2 行是重数。
输入文件示例 输出文件示例
input.txt output.txt
6 2
1 3
2
2
2
3
5
#include
#include
using namespace std;
const int N = 1e5 + 10;
const int INF = 0x7f7f7f;
typedef struct node{
int num;
int index;
}node;
node a[N];
bool cmp(node aa,node bb)
{
return aa.num>bb.num;
}
int main()
{
int n,x;
cin >> n;
for(int i = 1 ; i <= n ; i ++ )
{
cin >> x;
a[x].num ++ ;
a[x].index = x;
}
sort(a,a+1010,cmp);
cout << a[0].index;
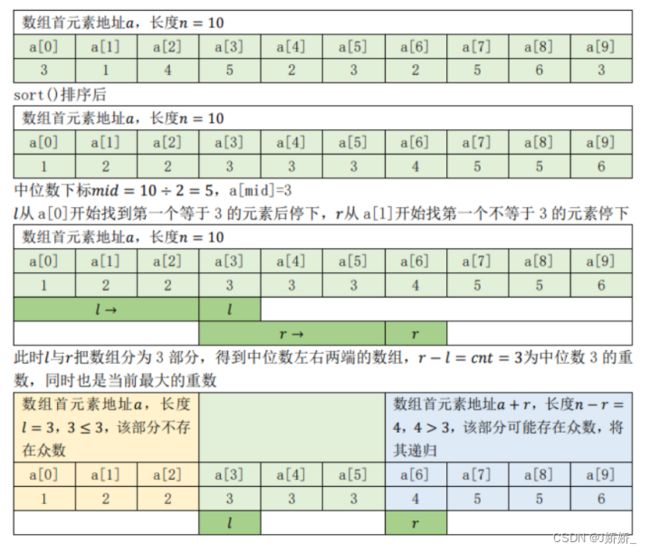
} 算法思路
先把数组排序Q,对于一个排好序的长度为数组a,我们可以通过中位数将数组分成3部分一中位数左边的部分、中位数、中位数右边
的部分:
用两个指针l和r分别指向中位数第一次出现的位置和最后一次出现的下一个位置,r-l即为该中位数的重数cnt,如果cnt大于当前最大
的重数maxcnt,我们就将该中位数更新为众数,cnt更新为maxcnt;
如果中位数左边部分的长度大于maxcnt,说明该部分可能存在众数,将其递归;
如果中位数右边部分的长度大于maxcnt,说明该部分可能存在众数,将其递归;
当递归不再进行时,说明整个数组的众数已找到。
实验3-3 最近点对问题
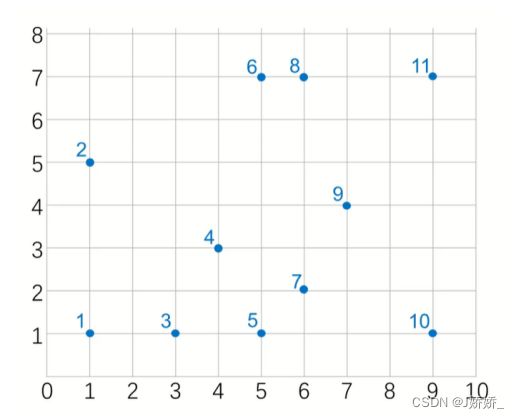
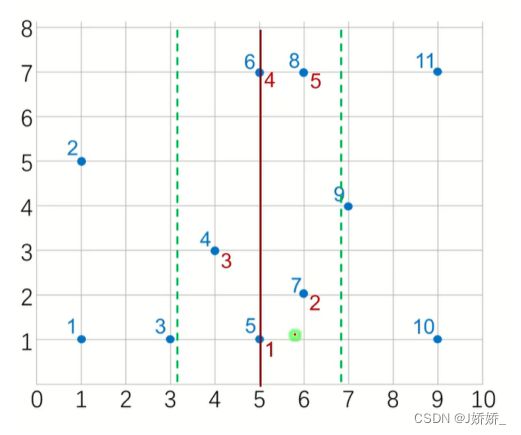
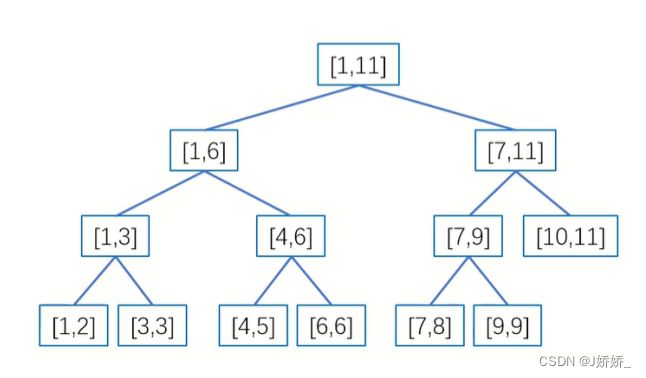
【问题描述】给定平面中的n个点,要求使用【分治策略】找到其中的一对点,使得在n个点对组成的所有点对中,该点对间的距离最小。
【输入形式】输入的第1行中有一个整数n,表示平面上点的个数;接下来的n行,每行有两个整数,分别表示一个点的横坐标和纵坐标。
【输出形式】输出1行一个浮点数,表示最接近点对的距离,结果保留2位小数。
【样例输入】
3
0 0
0 1
0 8
【样例输出】
1.00
借鉴平面最近点对的分治做法及其证明_第二题(较难,选做题,做出来的加3分)题目描述给定平面上n个点,找出其中的一对-CSDN博客
#include
#include
#include
#include
using namespace std;
#define Inf 1<<31-1
struct node{
double x;
double y;
};
const int N=300005;
struct node point[N];
int mpt[N];
double dis(node a,node b)
{
return sqrt((a.x-b.x)*(a.x-b.x)+(a.y-b.y)*(a.y-b.y));
}
bool cmp1(node a,node b)
{
if(a.x==b.x)return a.y>1;
double d1=run(mid,right);
double d2=run(left,mid-1);
double minn=min(d1,d2);
int k=0;
for(int i=left;i<=right;i++)
{
if(fabs(point[mid].x-point[i].x)<=minn)
{
mpt[++k]=i;
}
}
sort(mpt+1,mpt+k+1,cmp2);
for(int i=1;i<=k;i++)
{
for(int j=i+1;j<=k && point[mpt[j]].y-point[mpt[i]].y<=minn;j++)
{
if(minn>=dis(point[mpt[i]],point[mpt[j]]))
minn=dis(point[mpt[i]],point[mpt[j]]);
}
}
return minn;
}
int main()
{
int n;
cin>>n;
for(int i=1;i<=n;i++)
{
cin>>point[i].x>>point[i].y;
}
sort(point+1,point+n+1,cmp1);
printf("%.2lf",run(1,n));
return 0;
} // 感觉从来都没写过最近点对问题的 O(nlgn) 做法
// 心血来潮,写一次
// Author: GGN_2015
// Date : 2022-03-23
// 基本思想:在回归时进行归并排序
// 从而保证合并在 O(n) 时间内完成
#include
#include
#include
using namespace std;
const int maxn = 100000 + 6;
const long long inf = 0x7f7f7f7f7f7f7f7fLL;
struct Point {int x, y;} ps[maxn]; // 用结构体储存所有的点坐标
Point Ltmp[maxn], Rtmp[maxn]; // 临时数组
int lcnt, rcnt;
bool cmpx(const Point& A, const Point& B) { // 按照 x 坐标进行排序
return A.x != B.x ? A.x < B.x : A.y < B.y;
}
long long sqr(int x) { // 计算平方(注意 long long)
return (long long)x * x;
}
long long dis(const Point& A, const Point& B) {
return sqr(A.x - B.x) + sqr(A.y - B.y); // 计算两点间距离的平方
}
void merge(int L, int mid, int R) { // 按照 y 坐标进行归并排序的合并操作
lcnt = 0; // 借用 Ltmp 临时数组进行归并排序
int i = L, j = mid + 1; // i, j 分别为左侧数组和右侧数组的 "当前元素"
while(i <= mid && j <= R) {
if(ps[i].y != ps[j].y ? ps[i].y < ps[j].y : ps[i].x < ps[j].x) {
// 按照 y 坐标从小到大排序
Ltmp[++ lcnt] = ps[i];
i ++;
}else {
Ltmp[++ lcnt] = ps[j];
j ++;
}
}
while(i <= mid) { // 左侧数组中仍有剩余元素
Ltmp[++ lcnt] = ps[i];
i ++;
}
while(j <= R) { // 右侧数组中仍有剩余元素
Ltmp[++ lcnt] = ps[j];
j ++;
}
for(int i = 1; i <= lcnt; i ++) { // 将临时数组中的数据拷贝回 ps 数组
ps[L + i - 1] = Ltmp[i];
}
}
long long solve(int L, int R) { // 递归计算区间 [L, R] 的最小距离,并将点按照 y 坐标排序
if(L >= R) return inf; // 空区间 / 只有一个节点的区间不需要计算
int mid = (L + R) / 2;
int midx = ps[mid].x;
long long lans = solve(L,mid); // 递归计算左半区间和右半区间
long long rans = solve(mid+1,R);
long long D = min(lans, rans);
long long mindis = inf;
lcnt = 0;
for(int i = L; i <= mid; i ++) { // 载入左半区间距中轴线距离 <= sqrt(mindis) 的点
if(sqr(midx - ps[i].x) <= D) {
Ltmp[++ lcnt] = ps[i];
}
}
rcnt = 0;
for(int i = mid+1; i <= R; i ++) {// 载入右半区间距中轴线距离 <= sqrt(mindis) 的点
if(sqr(ps[i].x - midx) <= D) {
Rtmp[++ rcnt] = ps[i];
}
}
// 注:Ltmp 和 Rtmp 中的数据是按照 Y 坐标有序的
int lpos = 1, rpos = 0;
for(int i = 1; i <= lcnt; i ++) { // 枚举 Ltmp 中的点的点
while(rpos < rcnt &&
(Rtmp[rpos + 1].y < Ltmp[i].y || sqr(Rtmp[rpos + 1].y - Ltmp[i].y) <= D)) {
rpos ++;
}
while(lpos < rcnt && Ltmp[i].y > Rtmp[lpos].y && sqr(Ltmp[i].y - Rtmp[lpos].y) > D) {
lpos ++;
}
for(int j = lpos; j <= rpos; j ++) { // Rtmp[lpos .. rpos] 是 日字形中的点
mindis = min(mindis, dis(Ltmp[i], Rtmp[j]));
}
}
merge(L, mid, R); // 归并排序的合并操作
return min(D, mindis);
}
int main() {
int n; scanf("%d", &n);
for(int i = 1; i <= n; i ++) { // 输入所有点的坐标
scanf("%d%d", &ps[i].x, &ps[i].y);
}
sort(ps + 1, ps + n + 1, cmpx); // 调了一下午发现忘排序了 ......
long long ans = solve(1, n); // 递归计算
printf("%.4lf\n", sqrt(ans)); // 输出最近点对距离
return 0;
} 实验3-4 最长递减子序列
【问题描述】
求一个数组的最长递减子序列。递减子序列指的是此子序列数字大小满足从大到小有序。例如序列(10,9,2,5,3,7,101,18),其递减子序列为(10,9,5,3),其长度为4。请使用动态规划设计算法,编程计算最长递减子序列长度。
【输入形式】
第1 行是正整数m(0≤m≤10000), 表示序列长度。下一行开始输出m个整数序列。
【输出形式】
程序运行结束时,将计算出的最长递减子序列长度输出。
【样例输入】
7
7 5 4 8 9 4 10
【样例输出】
3
【样例说明】
【评分标准】
#include
using namespace std;
const int N = 1e5 + 10;
int a[N],dp[N];
int main()
{
int n;
cin >> n;
for(int i = 1; i <= n ; i ++ )
{
cin >> a[i];
}
for(int i = 1; i <= n ; i ++ )
{
dp[i] = 1;
for(int j = 1; j < i; j ++)
{
if(a[j] > a[i])
{
dp[i] = max(dp[i] ,dp[j] + 1 );
}
}
}
int maxn = dp[1];
for(int i = 2 ; i <= n ; i ++ )
{
maxn = max(maxn , dp[i]);
}
cout << maxn ;
return 0;
}