并行程序设计实验——高斯消元

并行程序设计实验——高斯消元

一、问题描述

熟悉高斯消元法解线性方程组的过程，然后实现SSE算法编程。过程中，自行构造合适的线性方程组，并选取至少2个角度，讨论不同算法策略对性能的影响。
可选角度包括但不限于以下几种选项：
①相同算法对于不同问题规模的性能提升是否有影响，影响情况如何；
②消元过程中采用向量编程的的性能提升情况如何；
③回代过程可否向量化，有的话性能提升情况如何；
④数据对齐与不对齐对计算性能有怎样的影响；
⑤SSE编程和AVX编程性能对比。

二、算法设计与实现

I. 串行消元算法实现

由于高斯消元有行主消元和列主消元两种形式，为了算法的运行效率，这里我采用的是行主消元

1. 用高斯消元法则实现普通串行消元算法的设计，时间复杂度$O(n^3)$

/**
 * 串行消元，这里加上了"等于号"后面的值这一列，便于求值，所以a的行是n，列是n+1
 * @param n 矩阵规模
 * @param a 将要消的矩阵
 */
void LU(int n, float a[][maxN]) {
    //依据上一行的数值进行消元
    for (int i = 0; i < n - 1; ++i) {
        //遍历一下所有行，将前i个都置为0
        for (int j = i + 1; j < n; ++j) {
            //求出相差倍数
            float temp = a[j][i] / a[i][i];

            //遍历这一行的所有值，将i后面的数值依次减去相对应的值乘以倍数
            for (int k = i + 1; k <= n; ++k) {
                a[j][k] -= a[i][k] * temp;
            }
            //第i个为0
            a[j][i] = 0.00;
        }
    }
}

2. 用高斯消元法之后的矩阵进行回代，则实现普通串行回代算法的设计，时间复杂度$O(n^2)$

/**
 * 回代函数，求出x的值
 * @param n 未知数个数
 * @param a 方程矩阵
 * @param x 未知数的值数组
 */
void generation(int n, float a[][maxN], float x[]) {
    //从最后一个未知数开始求，依次向上求解
    for (int i = n - 1; i >= 0; --i) {
        // 未知数等于"等于号"后面的值除以系数
        x[i] = a[i][n] / a[i][i];
        for (int j = i - 1; j >= 0; --j) {
            // 求出x[i]后，依次代入上面的每一个方程，更新"等于号"后面的值
            a[j][n] -= x[i] * a[j][i];
        }
    }
}

II. SSE消元算法实现

1. 利用SSE函数的思想，按照串行算法的思路，每四个一组进行计算，时间复杂度$O(n^3)$

/**
 * SSE算法消元设计
 * @param n 矩阵规模
 * @param a 方程矩阵，规模是（n，n+1）
 */
void SSE_LU(int n, float a[][maxN]) {
    float temp;
    __m128 div, t1, t2, sub;
    for (int i = 0; i < n - 1; ++i) {
        for (int j = i + 1; j < n; ++j) {
            // 用temp暂存相差的倍数
            temp = a[j][i] / a[i][i];
            // div全部用于存储temp，方便后面计算
            div = _mm_set1_ps(temp);
            
            //每四个一组进行计算，思想和串行类似
            int k = n - 3;
            for (; k >= i + 1; k -= 4) {
                t1 = _mm_loadu_ps(a[i] + k);
                t2 = _mm_loadu_ps(a[j] + k);
                sub = _mm_sub_ps(t2, _mm_mul_ps(t1, div));
                _mm_store_ss(a[j] + k, sub);
            }
            //处理剩余部分
            for (k += 3; k >= i + 1; --k) { 
                a[j][k] -= a[i][k] * temp;
            }
            a[j][i] = 0.00;
        }
    }
}

2. 利用SSE函数实现回代过程的向量化。这里需要特别注意的是，由于我写的是列消元，所以对回代过程进行向量化的过程中，需要先将矩阵转置。时间复杂度$O(n^2)$

/**
 * SSE实现回代过程向量化
 * @param n 未知数个数
 * @param a 方程矩阵
 * @param b 未知数的值数组
 */
void SSU_generation(int n, float a[][maxN], float b[]) {
    __m128 temp, t1, t2, sub;
    for (int i = n - 1; i >= 0; --i) {
        b[i] = a[i][n] / a[i][i];
        temp = _mm_set1_ps(b[i]);
        // 和串行算法思路类似，这里先将矩阵转置，方便计算
        for (int k = 0; k < i; ++k) {
            swap(a[k][n], a[n][k]);
            swap(a[k][i], a[i][k]);
        }
        //每四个一组进行计算
        int j = i - 4;
        for (; j >= 0; j -= 4) {
            t1 = _mm_loadu_ps(a[i] + j);
            t2 = _mm_loadu_ps(a[n] + j);
            sub = _mm_sub_ps(t2, _mm_mul_ps(t1, temp));
            _mm_store_ss(a[n] + j, sub);
        }
        //处理剩余部分
        for (j += 3; j >= 0; --j) { 
            a[n][j] -= a[i][j] * b[i];
        }
        //转置回来
        for (int k = 0; k < i; ++k) {
            swap(a[k][n], a[n][k]);
            swap(a[k][i], a[i][k]);
        }
    }
}

II. 主函数算法设计

1. 计时函数

• 计时函数采用sys/time.h库中的gettimeofday函数，该函数的精确度可以打到微妙级别，所以对函数的运行时间可以很好的估量
• 我还设置了多组循环实验，每一次循环将产生不同的矩阵，每一组矩阵乘法算法重复运行Counts次，然后得到平均估值，这样可以很好地减少一定量的误差

2. 规模自增

• 为了更好地对比四种算法的运行效率，我设计了一个GapSize值，用于矩阵规模每一次都自增GapSize，直到达到最大值。
• 另外，这里的区间个数自由度非常高，我们可以任意设置区间个数SizeCounts，以便帮助我们更好地比较算法之间的差异

const int maxN = 1026; // 矩阵的最大值
int GapSize = 128;//设置间隙大小，每一个矩阵规模自增GapSize
int SizeCounts = 10;//设置区间个数，可以自由调整
int Counts = 50;//设置每次循环的次数
float a[maxN][maxN];
float b[maxN];
float tempA[maxN][maxN];//用于暂时存储a数组的值，控制变量唯一

//用于矩阵改变数值,为防止数据溢出,随机数的区间为100以内的浮点数
void change(int n, float a[][maxN]) {
    srand((unsigned) time(NULL));
    for (int i = 0; i < n; i++) {
        for (int j = 0; j <= n; j++) {
            a[i][j] = (float) (rand() % 10000) / 100.00;
        }
    }
}

//用于暂时存储a数组，控制变量
void store(int n, float a[][maxN], float b[][maxN]) {
    for (int i = 0; i < n; ++i) {
        for (int j = 0; j <= n; ++j) {
            b[i][j] = a[i][j];
        }
    }
}

int main(int arg, char *argv[]) {
    //设置初始时间和结束时间
    struct timeval startTime, stopTime;
    for (int nowSize = GapSize, counts = 1; counts <= SizeCounts; nowSize += GapSize, counts++) {
        cout << "size: " << nowSize << endl;
        //设置每一个矩阵规模的总时间,每一个循环都加入到改变量中
        double eli_time = 0, solve_time = 0, sse_eli_time = 0, sse_solve_time = 0;
        //循环Counts次
        for (int i = 0; i < Counts; ++i) {
            change(nowSize, a);
            store(nowSize, a, tempA);//暂时将a数组存储在tempA中
            //计算串行消元时间
            gettimeofday(&startTime, NULL);
            LU(nowSize, a);
            gettimeofday(&stopTime, NULL);
            eli_time += (stopTime.tv_sec - startTime.tv_sec) * 1000 +
                        (double) (stopTime.tv_usec - startTime.tv_usec) * 0.001;
            //计算串行回代时间
            gettimeofday(&startTime, NULL);
            generation(nowSize, a, b);
            gettimeofday(&stopTime, NULL);
            solve_time += (stopTime.tv_sec - startTime.tv_sec) * 1000 +
                          (double) (stopTime.tv_usec - startTime.tv_usec) * 0.001;

            //计算SSE消元时间
            gettimeofday(&startTime, NULL);
            SSE_LU(nowSize, tempA);
            gettimeofday(&stopTime, NULL);
            sse_eli_time += (stopTime.tv_sec - startTime.tv_sec) * 1000 +
                            (double) (stopTime.tv_usec - startTime.tv_usec) * 0.001;
            //计算SSE回代时间
            gettimeofday(&startTime, NULL);
            SSE_generation(nowSize, tempA, b);
            gettimeofday(&stopTime, NULL);
            sse_solve_time += (stopTime.tv_sec - startTime.tv_sec) * 1000 +
                              (double) (stopTime.tv_usec - startTime.tv_usec) * 0.001;
        }
        cout << "串行消元时间：" << eli_time / Counts << "ms" << endl;
        cout << "串行回代时间：" << solve_time / Counts << "ms" << endl;
        cout << "并行消元时间：" << sse_eli_time / Counts << "ms" << endl;
        cout << "并行回代时间：" << sse_solve_time / Counts << "ms" << endl;
        cout << endl;
    }
}

三、实现结果和分析

以上是我程序运行结果，为了方便查看，我做成了echarts表格(由于我重新运行了一次，实验结果可能稍有不同)

1. 比较串行消元和SSE消元

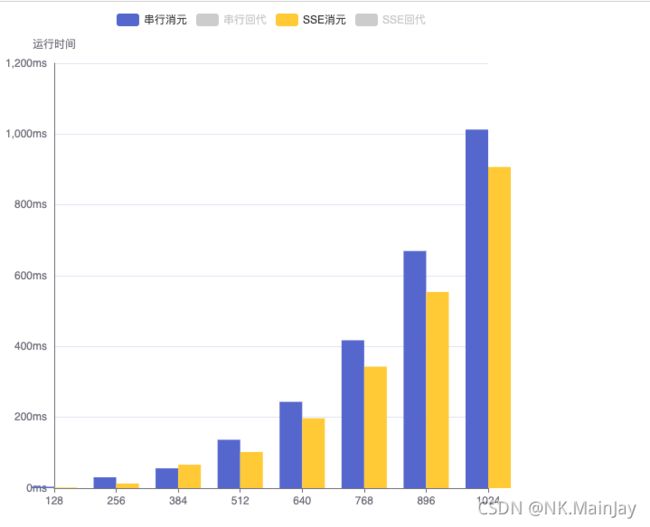
由图可知，SSE算法的消元总体来说是运行效率是高于串行算法的。且随着矩阵规模增大而增大。总体其实并没有相差特别大。可能是一部分原因因为我自己写的串行算法本身运行效率还不错
2. 首先比较串行回代和SSE回代

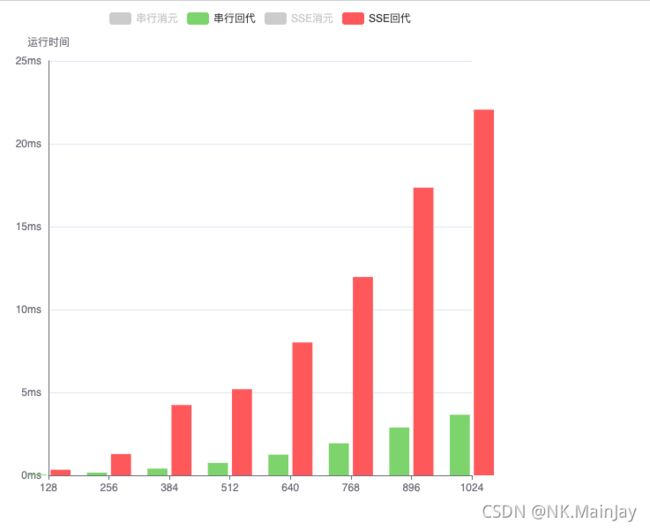
这个差距就有点相差的过于明显，SSE算法的回代竟然比串行算法的回代运行效率还要慢。猜想其中可能一部分原因是因为我使用的SSE算法回代过程中转置过程本身就比较耗费时间

结论分析

1. 相同算法对于不同问题规模的性能提升有一定的影响，但是影响效果不大
2. 消元过程中采用向量编程的的性能提升情况效果一般，总体感觉提升不大（可能和自己写的有关）
3. 回代过程也可以向量化，但是对性能提升情况效果不佳；
4. 总体来说，SSE算法对运行效率还是有一定程度的提升。关键在于你怎么优化运行效率

四、源代码

源代码