VC++中使用OpenCV对原图像中的四边形区域做透视变换

VC++中使用OpenCV对原图像中的四边形区域做透视变换

最近闲着跟着油管博主murtazahassan，学习了一下LEARN OPENCV C++ in 4 HOURS | Including 3x Projects | Computer Vision，对应的Github源代码地址为：Learn-OpenCV-cpp-in-4-Hours

视频里面讲到到原图中的扑克牌四个顶点标记画圆，并且将扑克牌K做透视变换后摆正重新显示，资源图像文件cards.png下载地址为：https://github.com/murtazahassan/Learn-OpenCV-cpp-in-4-Hours/tree/main/Resources

什么是透视变换

从名称中可以清楚地看出，透视变换与视点的变化相关。这种类型的转换不保留平行度、长度和角度。但它们确实保留了共线性和关联性。这意味着即使在变换之后直线仍将保持直线。

一般来说，透视变换可以表示为：

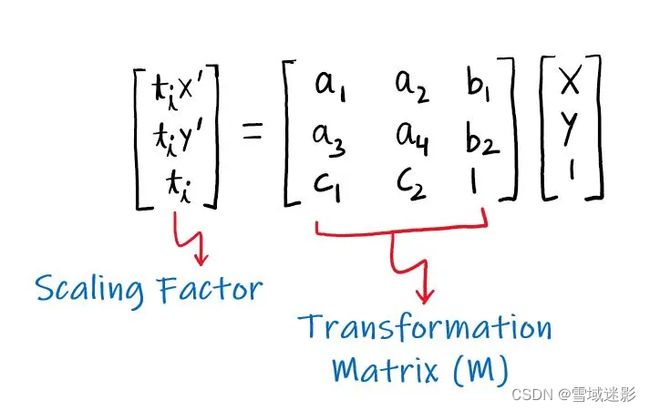
上面是透视变换的数学形式，说白了就是对图像中的某个区域做处理。
这里，（x’，y’）是变换点，而（x，y）是输入点。变换矩阵 (M) 可以看作是以下的组合：

对于仿射变换，投影向量等于0。因此，仿射变换可以被认为是透视变换的特例。

由于变换矩阵（M）由8个常数（自由度）定义，因此为了找到这个矩阵，我们首先在输入图像中选择4个点，然后根据用途将这4个点映射到未知输出图像中的所需位置-case（这样我们将有 8 个方程和 8 个未知数，并且可以很容易地求解）。

一旦计算出变换矩阵，我们就将透视变换应用于整个输入图像以获得最终的变换图像。让我们看看如何使用 OpenCV 来做到这一点。

OpenCV中的透视变换相关函数getPerspectiveTransform和warpPerspective

透视变换(Perspective Transformation)是将成像投影到一个新的视平面(Viewing Plane)，也称作投影映射(Projective Mapping)。如图1，通过透视变换ABC变换到A’B’C’。透视变换是计算图像学和线性代数中的一个常用概念。
在视角转换中，我们可以改变给定图像或视频的视角，以便更好地洞察所需信息。在透视变换中，我们需要提供图像上想要通过改变透视来收集信息的点。我们还需要提供要在其中显示图像的点。然后，我们从给定的两组点获得透视变换并将其与原始图像包裹起来。

我们使用 getPerspectiveTransform， 然后使用 warpPerspective 函数，其中 getPerspectiveTransform它将 4 对对应点作为输入并输出变换矩阵，计算出变换矩阵 (M) 后，将其传递给 warpPerspective() 函数，该函数将透视变换应用于图像。

getPerspectiveTransform的函数有两种重载形式，其中一个函数原型如下：

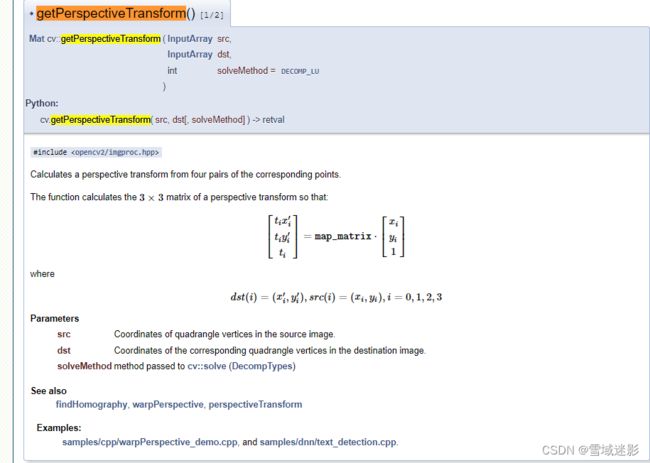
getPerspectiveTransform其重载函数原型2为：

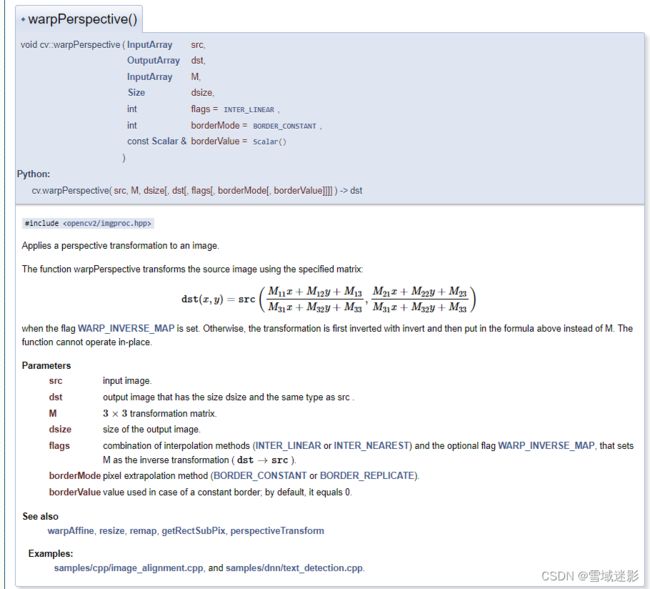
warpPerspective 函数原型为：

首先使用Windows电脑自带默认的画图工具打开cards.png原图，通过移动鼠标到扑克牌K的左上、右上、左下、右下角，在左下角即可查看图像某点的像素坐标，如下图所示：

可以看到K的左上角坐标为：{529, 144}
用同样的方法，依次获取K的右上、左下、右下角坐标，分别为：{771,190}、{405,395}、{674,457}

实现代码

1、根据原图，以及卡片K的位置，获取对应的透视变换矩阵
2、 对原图中的卡片K根据透视变化矩阵进行转换，得到目标图像imgWarp
3、在原图K的四个顶点位置处画一个圆，半径为10像素，颜色为红色
4、显示原图和目标图像K
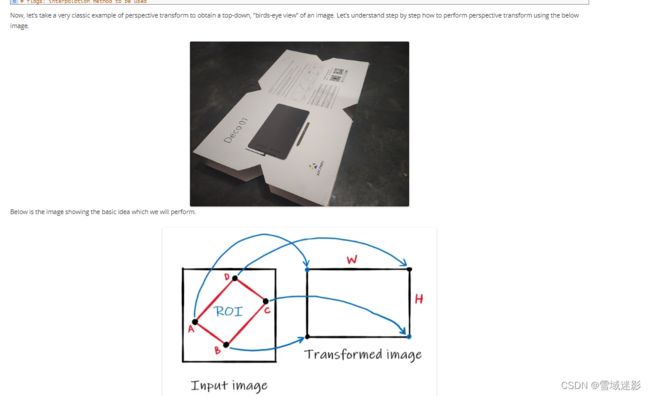
我们要将扑克牌K进行透视变换摆正，类似下图的转换，以获得图像的自上而下的“鸟瞰图”。：

实现代码如下：

#include 
#include 
#include 
#include 

using namespace cv;
using namespace std;

///  Warp Images  //

int main()
{

	string path = "Resources/cards.jpg";
	Mat img = imread(path);	// 读取原图
	Mat matrix, imgWarp;
	float w = 250, h = 350;	// 目标图像的宽度和高度

	Point2f src[4] = { {529,144},{771,190},{405,395},{674,457} };	// 扑克牌K的四个顶点坐标，分别为左上、右上、左下、右下角坐标
	Point2f dst[4] = { {0.0f,0.0f},{w,0.0f},{0.0f,h},{w,h} };		// 目标输出图像imgWarp的四个顶点坐标

	matrix = getPerspectiveTransform(src, dst);	// 根据原图和目标图，获取对应透视变换的转换矩阵
	warpPerspective(img, imgWarp, matrix, Point(w, h));	// 对原图中的卡片K根据透视变化矩阵进行转换，得到目标图像imgWarp

	// 在原图K的四个顶点位置处画一个圆，半径为10像素，颜色为红色
	for (int i = 0; i < 4; i++)
	{
		circle(img, src[i], 10, Scalar(0, 0, 255), FILLED);
	}

	imshow("Image", img);			// 显示原图
	imshow("Image Warp", imgWarp);	// 显示目标图像K
	waitKey(0); // 永久等待直到用户按下键盘中的键，则退出程序

	return 0;
}

运行结果

在VS2017中运行结果如下图所示：

对原图中的扑克片K、J、9、Q依次做透视变化并输出

接下来，我们参照上面扑克牌K的处理方法，可以依次对原图中的扑克牌J、9、Q做类似的处理，代码如下图所示:

#include 
#include 
#include 
#include 

using namespace cv;
using namespace std;

///  Warp Images  //

int main()
{

	string path = "Resources/cards.jpg";
	Mat img = imread(path);
	Mat matrix, imgWarpK;
	Mat matrixJ, imgWarpJ;
	Mat matrix9, imgWarp9;
	Mat matrixQ, imgWarpQ;
	float w = 250, h = 350;	// 目标卡片显示的宽度和高度

	// 1.处理卡片K
	// 分别对应扑克牌K的左上、右上、左下、右下角的坐标
	Point2f src[4] = { {529,144},{771,190},{405,395},{674,457} };	// 源图像中K卡片对应的四边形顶点的坐标。
	Point2f dst[4] = { {0.0f,0.0f},{w,0.0f},{0.0f,h},{w,h} };		// 目标图像中K卡片对应的四边形顶点的坐标。

	// 获取透视变换矩阵
	matrix = getPerspectiveTransform(src, dst);
	warpPerspective(img, imgWarpK, matrix, Point(w, h));

	// 在原图K的四个顶点处画圆
	for (int i = 0; i < 4; i++)
	{
		circle(img, src[i], 10, Scalar(0, 0, 255), FILLED);
	}

	// 2.处理卡片J
	// 分别对应扑克牌J的左上、右上、左下、右下角的坐标
	Point2f srcOfJCard[4] = { {776, 108}, {1018, 85}, {849, 358}, {1116, 331} };
	Point2f destOfJCard[4] = { {0.0f, 0.0f}, {w, 0.0f}, {0.0f, h}, {w, h} };

	// 获取卡片J的透视变化矩阵
	matrixJ = getPerspectiveTransform(srcOfJCard, destOfJCard);
	warpPerspective(img, imgWarpJ, matrixJ, Point(w, h));

	// 在原图J的四个顶点画圆
	for (int i = 0; i < 4; i++) {
		circle(img, srcOfJCard[i], 10, Scalar(255, 0, 0), FILLED);
	}

	// 3.处理卡片9
	// 分别对应扑克牌9的左上、右上、左下、右下角的坐标
	Point2f srcOf9Card[4] = { {743, 383}, {1023, 438}, {646, 710}, {962, 781} };
	Point2f destOf9Card[4] = { {0.0f, 0.0f}, {w, 0.0f}, {0.0f, h}, {w, h} };

	// 获取卡片9的透视变化矩阵
	matrix9 = getPerspectiveTransform(srcOf9Card, destOf9Card);
	warpPerspective(img, imgWarp9, matrix9, Point(w, h));

	// 在原图9的四个顶点画圆
	for (int i = 0; i < 4; i++) {
		circle(img, srcOf9Card[i], 10, Scalar(0, 255, 0), FILLED);
	}

	// 4.处理卡片Q
	// 分别对应扑克牌Q的左上、右上、左下、右下角的坐标
	Point2f srcOfQCard[4] = { {64, 326}, {339, 279}, {91, 636}, {401, 573} };
	Point2f destOfQCard[4] = { {0.0f, 0.0f}, {w, 0.0f}, {0.0f, h}, {w, h} };

	// 获取卡片Q的透视变化矩阵
	matrixQ = getPerspectiveTransform(srcOfQCard, destOfQCard);
	warpPerspective(img, imgWarpQ, matrixQ, Point(w, h));

	// 在原图Q的四个顶点画圆
	for (int i = 0; i < 4; i++) {
		circle(img, srcOfQCard[i], 10, Scalar(0, 255, 0), FILLED);
	}


	imshow("Image", img);			// 显示原图
	imshow("Warp K", imgWarpK);		// 显示经透视变化后的卡片K，宽度为250，高度为350
	imshow("Warp J", imgWarpJ);		// 显示经透视变化后的卡片J，宽度为250，高度为350
	imshow("Warp 9", imgWarp9);		// 显示经透视变化后的卡片9，宽度为250，高度为350
	imshow("Warp Q", imgWarpQ);     // 显示经透视变化后的卡片Q，宽度为250，高度为350

	waitKey(0);	// 无限期的等待键盘输入


	return 0;
}

对应的运行结果如下图所示：

参考资料

• Perspective Transformation – Python OpenCV
• TAG ARCHIVES: CV2.GETPERSPECTIVETRANSFORM()
• LEARN OPENCV C++ in 4 HOURS | Including 3x Projects | Computer Vision
• murtazahassan/Learn-OpenCV-cpp-in-4-Hours
• OpenCV官网
• OpenCV-Get Started
• OpenCV Github仓库源代码
• OpenCV tutorial
• Warp Images
• https://docs.opencv.org/4.x/da/d54/group__imgproc__transform.html