算法笔记(动态规划入门题)

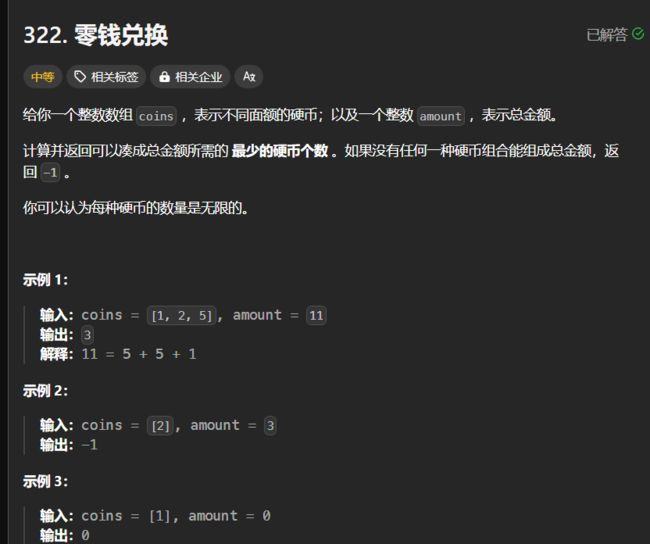
1.找零钱

int coinChange(int* coins, int coinsSize, int amount) {
    int dp[amount + 1];
    memset(dp,-1,sizeof(dp));
    dp[0] = 0;
    for (int i = 1; i <= amount; i++)
        for (int j = 0; j < coinsSize; j++)
            if (coins[j] <= i && dp[i - coins[j]] != -1)
                if (dp[i] == -1 || dp[i] > dp[i - coins[j]] + 1)
                    dp[i] = dp[i - coins[j]] + 1;
    return dp[amount];
}

2.有奖问答

#include 
using namespace std;
int ans=0;
int dp[31][10];//dp[i][j]代表回答了i道题目时得到了j*10的分数的 总方案数
int main(){
  dp[0][0] = 1;//初始化起点,起点就表示一个方案数
  for(int i = 1;i<=30;i++)
    for(int j = 0;j<=9;j++)
      if(j==0)//得到零分，说明这一题答错了，那么方案数量就是上一题的所有方案之和，上一题多少分都不影响当前题，因为一旦答错，分数归零。
        for(int k = 0;k<=9;k++)
          dp[i][j] += dp[i-1][k];
      else//答对了，那么说明这个方案必须承接上一次答对的方案数，上一题必须是当前分数-10，即j-1道题。
        dp[i][j] = dp[i-1][j-1];
  for(int i = 0;i<=30;i++)
    ans+=dp[i][7];//记录所有答对7次的方案数
  cout<

3.字符串转换

#include 
#include 
#include 
using namespace std;
string s,t;
int transform(){
  int l1=s.length(),l2=t.length();
  int dp[l1+1][l2+1];
  for(int i=0;i>s>>t;
  printf("%d",transform());
  return 0;
}

动态规划浅析——记一道困难的字符串操作数问题 - 知乎 (zhihu.com)这个文章写的很不错，可以看看。

4.完全背包问题

#include 
#include 
#include 
using namespace std;
int n,v;
struct obj{
  int v;//体积
  int c;//价值
};
int packet(obj o[]){
  int dp[n+1][v+1];//选第i个物品且体积为j时的价值
  memset(dp,0,sizeof(dp));
  for(int i=1;i<=n;i++){
    for(int j=0;j<=v;j++){
      dp[i][j]=dp[i-1][j];
      for(int k=0;k*o[i].v<=j;k++){
        dp[i][j]=max(dp[i][j],dp[i-1][j-k*o[i].v]+k*o[i].c);
      }
    }
  }
  return dp[n][v];
}
int main()
{
  // 请在此输入您的代码
  scanf("%d%d",&n,&v);
  obj o[n+1];
  o[0].v=0,o[0].c=0;
  for(int i=1;i<=n;i++)
    scanf("%d%d",&o[i].v,&o[i].c);
  printf("%d",packet(o));
  return 0;
}

5.松散子序列

#include 
#include 
#include 
using namespace std;
string s;
inline int value(char a){
  return a-'a'+1;
}
int SubSeq(){
  int len=s.length();
  int dp[len];
  memset(dp,0,sizeof(dp));
  dp[0]=value(s[0]);
  dp[1]=max(dp[0],value(s[1]));
  for(int i=2;i>s;
  cout<

————部分代码是别人写的题解，本人仅为转载，非原创；