Python数学建模之核心工具库
1.NumPy
1.功能简介
NumPy 是 Python 用于科学计算的基础工具库。它主要包含四大功能:
(1)强大的多维数组对象;
(2)复杂的函数功能;
(3)集成 C / C ++和 FORTRAN 代码的工具;
(4)有用的线性代数、傅里叶变换和随机数功能等。
NumPy 提供了两种基本的对象:ndarray 和 ufunc。ndarray 存储单一数据类型的多维数组,ufunc 是能够对数组进行处理的函数。
2.函数的导入
导入 NumPy 工具库时,一般改变其名称为 np :
import numpy as np3.数组的创建
1.使用array()
使用 array() 将列表或元组转换为 ndarray 数组,调用格式为:
array(object, dtype=None, copy=True, order='K', subok=False, ndmin=0)
object:表示要转换为 ndarray 数组的列表或元组。
dtype:表示指定转换后的数组的数据类型。默认为 None。
copy:表示是否复制输入的对象。默认为 True,即进行复制。
order:表示创建数组时的存储顺序。默认为 'K',表示数组在内存中以尽可能紧凑的方式存储,即按照最佳存储顺序存储数组。
subok:表示是否允许子类继承 ndarray 类。默认为 False,即不允许。
ndmin:表示要创建的数组的最小维度。默认为 0,即根据输入的对象自动确定数组的维度。
示例代码:
import numpy as np
# 将列表转换为ndarray数组
list1 = [1, 2, 3, 4, 5]
array1 = np.array(list1)
# 将元组转换为ndarray数组
tuple1 = (6, 7, 8, 9, 10)
array2 = np.array(tuple1)
# 按指定数据类型生成新的数组
array3 = array1.astype(float)
# 生成指定数据类型的数组
list2 = [1.1, 2.2, 3.3, 4.4, 5.5]
array4 = np.array(list2, dtype=int)
# 指定存储顺序(列优先)和最小维度
list3 = [[1, 2], [3, 4], [5, 6]]
array5 = np.array(list3, order='F', ndmin=2)
print(array1); print(array2); print(array3); print(array4); print(array5)运行结果:
[1 2 3 4 5]
[ 6 7 8 9 10]
[1. 2. 3. 4. 5.]
[1 2 3 4 5]
[[1 2]
[3 4]
[5 6]]2.使用arrange()
使用 arrange() 在给定区间内创建等差数组,调用格式为:
arange(start=0, stop=None, step=1, dtype=None)start:表示等差数组的起始值。如果未指定,则默认为0。
stop:表示等差数组的终止值(不包含在数组中)。
step:表示等差数组的步长。如果未指定,则默认为1。
dtype:表示指定数组的数据类型。默认为 None,即根据输入的值自动推导。
示例代码:
import numpy as np
# 创建从0到4的等差数组,默认步长为1
array1 = np.arange(5)
# 创建从2到10的等差数组,步长为2
array2 = np.arange(2, 11, 2)
# 创建从1到10的等差数组,步长为1.5,指定数据类型为float
array3 = np.arange(1, 10, 1.5, dtype=float)
print(array1); print(array2); print(array3)运行结果:
[0 1 2 3 4]
[ 2 4 6 8 10]
[1. 2.5 4. 5.5 7. 8.5]
3.使用linspace()
使用 linspace() 在给定区间内创建 num 个数据的等差数组,调用格式为:
linspace(start, stop, num=50, endpoint=True, retstep=False, dtype=None)
start:表示等差数组的起始值。
stop:表示等差数组的终止值。
num:表示要生成的等差数组中的数据个数,默认为 50。
endpoint:表示是否将 stop 值包含在数组中,默认为 True,即包含。
retstep:表示是否返回等差步长,默认为 False,即不返回。
dtype:表示指定数组的数据类型,默认为 None,即根据输入的值自动推导。
示例代码:
import numpy as np
# 创建从0到10的等差数组,包含5个数据
array1 = np.linspace(0, 10, num=5)
# 创建从2到10的等差数组,包含10个数据,且不包含终止值
array2 = np.linspace(2, 10, num=10, endpoint=False)
# 创建从1到10的等差数组,包含7个数据,返回步长
array3, step = np.linspace(1, 10, num=7, retstep=True)
print(array1); print(array2); print(array3, step)运行结果:
[ 0. 2.5 5. 7.5 10. ]
[2. 2.8 3.6 4.4 5.2 6. 6.8 7.6 8.4 9.2]
[ 1. 2.5 4. 5.5 7. 8.5 10. ] 1.54.使用logspace()
使用 logspace() 在给定区间上生成等比数组,调用格式为:
logspace(start, stop, num=50, endpoint=True, base=10.0, dtype=None)start:表示等比数组的起始值。
stop:表示等比数组的终止值。
num:表示要生成的等比数组中的数据个数,默认为 50。
endpoint:表示是否将 stop 值包含在数组中,默认为 True,即包含。
base:表示等比数列的底数,默认为 10.0,即以 10 为底数。
dtype:表示指定数组的数据类型,默认为 None,即根据输入的值自动推导。
示例代码:
import numpy as np
# 在10的0次方到10的2次方之间生成包含5个数据的等比数组
array1 = np.logspace(0, 2, num=5)
# 在2的0次方到2的4次方之间生成包含6个数据的等比数组,且不包含终止值
array2 = np.logspace(0, 4, num=6, endpoint=False, base=2)
# 在1的-2次方到1的2次方之间生成包含7个数据的等比数组,以e为底数
array3 = np.logspace(-2, 2, num=7, base=np.e)
print(array1); print(array2); print(array3)运行结果:
[ 1. 3.16227766 10. 31.6227766 100. ]
[ 1. 1.58740105 2.5198421 4. 6.34960421 10.0793684 ]
[0.13533528 0.26359714 0.51341712 1. 1.94773404 3.79366789
7.3890561 ]5.使用ones()、zeros()、empty()、ones_like()等函数
1.ones()、zeros()、empty()
使用 ones() 生成指定维数,元素值全为 1 的数组,调用格式为:
ones(shape, dtype=None, order='C')
shape:表示生成数组的形状,可以是一个整数,表示生成一个一维数组,或者是一个整数元组,表示生成一个多维数组。
dtype:表示指定数组的数据类型,默认为 None,即使用默认的数据类型。
order:表示数组在内存中的存储顺序,默认为 'C',表示按行存储。
示例代码:
import numpy as np
# 生成一个一维数组,包含5个元素,元素值全部为1
array1 = np.ones(5)
# 生成一个二维数组,形状为(3, 4),元素值全部为1
array2 = np.ones((3, 4))
# 生成一个三维数组,形状为(2, 3, 2),元素值全部为1
array3 = np.ones((2, 3, 2))
print('array1:\n',array1); print('array2:\n',array2); print('array3:\n',array3)运行结果:
array1:
[1. 1. 1. 1. 1.]
array2:
[[1. 1. 1. 1.]
[1. 1. 1. 1.]
[1. 1. 1. 1.]]
array3:
[[[1. 1.]
[1. 1.]
[1. 1.]]
[[1. 1.]
[1. 1.]
[1. 1.]]]zeros() 和 empty() 的用法与 ones() 相同,只不过 zeros() 生成数组的元素值全为 0 ,empty()生成数组元素的值是随机数。
2.eyes()
使用 eyes() 生成指定维数,指定对角线元素值全为 1 的数组,调用格式为:
eye(N, M=None, k=0, dtype=float, order='C')N:表示生成数组的行数(或列数,如果 M 未指定)。
M:可选参数,表示生成数组的列数,默认为 None,即默认与行数 N 相等。
k:可选参数,表示从主对角线偏移的次数,默认为 0,表示主对角线。k为正值表示主对角线向上偏移,k为负值表示主对角线向下偏移。
dtype:表示指定数组的数据类型,默认为 float。
order:表示数组在内存中的存储顺序,默认为 'C',表示按行存储。
示例代码:
import numpy as np
# 生成一个形状为(3, 3)的二维数组,主对角线上的元素值为1,其余元素值为0
array1 = np.eye(3)
# 生成一个形状为(4, 5)的二维数组,主对角线上的元素值为1,其余元素值为0
array2 = np.eye(4, 5)
# 生成一个形状为(5, 5)的二维数组,主对角线上的元素值为1,上方和下方各偏移一次的对角线上元素值为1
array3 = np.eye(5, k=1)
# 生成一个形状为(3, 3)的二维数组,数据类型为整数,主对角线上的元素值为1,其余元素值为0
array4 = np.eye(3, dtype=int)
# 生成一个形状为(3, 3)的二维数组,以列优先方式存储,主对角线上的元素值为1,其余元素值为0
array5 = np.eye(3, order='F')
print('array1:\n',array1); print('array2:\n',array2); print('array3:\n',array3); print('array4:\n',array4); print('array5:\n',array5)
运行结果:
array1:
[[1. 0. 0.]
[0. 1. 0.]
[0. 0. 1.]]
array2:
[[1. 0. 0. 0. 0.]
[0. 1. 0. 0. 0.]
[0. 0. 1. 0. 0.]
[0. 0. 0. 1. 0.]]
array3:
[[0. 1. 0. 0. 0.]
[0. 0. 1. 0. 0.]
[0. 0. 0. 1. 0.]
[0. 0. 0. 0. 1.]
[0. 0. 0. 0. 0.]]
array4:
[[1 0 0]
[0 1 0]
[0 0 1]]
array5:
[[1. 0. 0.]
[0. 1. 0.]
[0. 0. 1.]]
3.ones_like()和zeros_like()
使用 ones_like() 函数生成一个与给定数组具有相同形状和数据类型的数组,调用格式为:
ones_like(a, dtype=None, order='K', subok=True, shape=None)a:表示输入的数组,用于确定生成数组的形状和数据类型。
dtype:可选参数,表示指定生成数组的数据类型,默认为 None,即与输入数组的数据类型相同。
order:表示数组在内存中的存储顺序,默认为 'K',即使用输入数组的存储顺序。
subok:表示生成的数组是否允许子类化,默认为 True,允许子类化。
shape:可选参数,表示生成数组的形状,默认为 None,即与输入数组的形状相同。
示例代码:
import numpy as np
# 生成一个与输入数组 a 形状相同的数组,元素值都为1
a = np.array([[2, 3, 4], [5, 6, 7]])
array1 = np.ones_like(a)
# 生成一个与输入数组 a 形状相同的数组,元素值都为1,数据类型为整数
array2 = np.ones_like(a, dtype=int)
# 生成一个与输入数组 a 形状相同的数组,元素值都为1,存储顺序为列优先
array3 = np.ones_like(a, order='F')
# 生成一个与输入数组 a 形状相同的数组,元素值都为1,不允许子类化
array4 = np.ones_like(a, subok=False)
# 生成一个形状为 (3, 2) 的数组,元素值都为1
array5 = np.ones_like(a, shape=(3, 2))
print('array1:\n',array1); print('array2:\n',array2); print('array3:\n',array3); print('array4:\n',array4); print('array5:\n',array5)
运行结果:
array1:
[[1 1 1]
[1 1 1]]
array2:
[[1 1 1]
[1 1 1]]
array3:
[[1 1 1]
[1 1 1]]
array4:
[[1 1 1]
[1 1 1]]
array5:
[[1 1]
[1 1]
[1 1]]
zeros_like() 函数用法与ones_like() 函数相同,只不过元素值为0。
4.数组元素的索引
二维数组元素的引用方式为a[i][j]或a[i,j],下面四种索引均以以下的二维数组为例:
import numpy as np
# 创建一个二维数组
a = np.array([[1, 2, 3],
[4, 5, 6],
[7, 8, 9]])
还可以用如下语句快速生成二维数组:
a = np.arange(16).reshape(4, 4) # 生成4行4列的数组,元素为0到151.整数索引
# 通过整数索引选择二维数组中的元素
print(a[0, 1]) # 输出:2
print(a[2, 2]) # 输出:92.切片索引
# 通过切片索引选择二维数组的行
print(a[1:3, :]) # 输出:[[4, 5, 6], [7, 8, 9]]
# 通过切片索引选择二维数组的列
print(a[:, 1:3]) # 输出:[[2, 3], [5, 6], [8, 9]]
# 通过切片索引选择二维数组的子矩阵
print(a[0:2, 1:3]) # 输出:[[2, 3], [5, 6]]3.布尔索引
# 通过布尔索引选择二维数组中符合条件的元素
mask = a > 5
print(a[mask]) # 输出:[6, 7, 8, 9]4.花式索引
# 通过花式索引选择二维数组中的指定元素
indices = [0, 2]
print(a[indices]) # 输出:[[1, 2, 3], [7, 8, 9]]5.矩阵合并与分割
1.矩阵的合并
vstack() 函数实现矩阵的上下合并,hstack()函数实现矩阵的左右合并。
调用格式:
numpy.vstack(tup)
numpy.hstack(tup) # tup 是一个包含多个数组的元组或列表,表示要合并的矩阵
代码示例:
import numpy as np
# 创建两个示例矩阵
matrix1 = np.array([[1, 2], [3, 4]])
matrix2 = np.array([[5, 6]])
# 使用 vstack() 函数进行上下合并
vstack_result = np.vstack((matrix1, matrix2))
print("上下合并结果:")
print(vstack_result)
# 使用 hstack() 函数进行左右合并
hstack_result = np.hstack((matrix1, matrix2.T))
print("左右合并结果:")
print(hstack_result)运行结果:
上下合并结果:
[[1 2]
[3 4]
[5 6]]
左右合并结果:
[[1 2 5]
[3 4 6]]2.矩阵的分割
vsplit(a, m) 把 a 平均分成 m 个行数组,hsplit(a, n )把 a 平均分成 n 个列数组。
代码示例:
import numpy as np
# 创建一个可被等分割的数组
arr = np.array([[1, 2, 3, 4],
[5, 6, 7, 8],
[9, 10, 11, 12],
[13, 14, 15, 16]])
# 使用 vsplit() 函数将数组分割成两个行数组
vsplit_result = np.vsplit(arr, 2)
print("行数组分割结果:")
for row_arr in vsplit_result:
print(row_arr)
# 使用 hsplit() 函数将数组分割成两个列数组
hsplit_result = np.hsplit(arr, 2)
print("列数组分割结果:")
for col_arr in hsplit_result:
print(col_arr)运行结果:
行数组分割结果:
[[1 2 3 4]
[5 6 7 8]]
[[ 9 10 11 12]
[13 14 15 16]]
列数组分割结果:
[[ 1 2]
[ 5 6]
[ 9 10]
[13 14]]
[[ 3 4]
[ 7 8]
[11 12]
[15 16]]6.矩阵的简单运算
1.求和
sum() 函数的调用格式:
numpy.sum(a, axis=None, dtype=None, keepdims=)
a:要求和的数组。
axis:指定要沿着哪个轴求和,默认值为 None,表示对整个数组进行求和。如果指定了轴值,将沿着该轴进行求和,返回的结果将减少一个维度。
dtype:指定返回的求和结果的数据类型,默认为 None,表示使用数组的数据类型。
keepdims:指定是否保持结果的维度,如果设置为 True,则结果将保持与输入数组相同的维度,默认值为
示例代码:
import numpy as np
# 创建一个数组
a = np.array([1, 2, 3, 4, 5])
# 对整个数组进行求和
sum_of_array = np.sum(a)
print("数组的和:", sum_of_array)
# 沿着轴 0 求和,即按列求和
sum_along_axis_0 = np.sum(a, axis=0)
print("按列求和:", sum_along_axis_0)
# 创建一个二维数组
b = np.array([[1, 2, 3],
[4, 5, 6]])
# 对整个二维数组求和
sum_of_matrix = np.sum(b)
print("二维数组的和:", sum_of_matrix)
# 沿着轴 0 求和,即按行求和
sum_along_axis_0 = np.sum(b, axis=0)
print("按行求和:", sum_along_axis_0)
# 沿着轴 1 求和,即按列求和
sum_along_axis_1 = np.sum(b, axis=1)
print("按列求和:", sum_along_axis_1)
运行结果:
数组的和: 15
按列求和: 15
二维数组的和: 21
按行求和: [5 7 9]
按列求和: [ 6 15]2.矩阵的逐个元素运算
对于维数相同的矩阵,矩阵的逐个元素运算可以直接用运算符,也可以调用函数。
示例代码:
import numpy as np
# 创建两个矩阵
matrix1 = np.array([[1, 2, 3],
[4, 5, 6]])
matrix2 = np.array([[7, 8, 9],
[10, 11, 12]])
# 逐个元素相加
add_result1 = np.add(matrix1, matrix2)
add_result2 = matrix1 + matrix2
print("逐个元素相加的结果1:")
print(add_result1)
print("逐个元素相加的结果2:")
print(add_result2)
# 逐个元素相减
subtract_result1 = np.subtract(matrix1, matrix2)
subtract_result2 = matrix1 - matrix2
print("逐个元素相减的结果1:")
print(subtract_result1)
print("逐个元素相减的结果2:")
print(subtract_result2)
# 逐个元素相乘
multiply_result1 = np.multiply(matrix1, matrix2)
multiply_result2 = matrix1 * matrix2
print("逐个元素相乘的结果1:")
print(multiply_result1)
print("逐个元素相乘的结果2:")
print(multiply_result2)
# 逐个元素相除
divide_result1 = np.divide(matrix1, matrix2)
divide_result2 = matrix1 / matrix2
print("逐个元素相除的结果1:")
print(divide_result1)
print("逐个元素相除的结果2:")
print(divide_result2)
# 逐个元素的乘幂
power_result1 = np.power(matrix1, matrix2)
power_result2 = matrix1 ** matrix2
print("逐个元素的乘幂的结果1:")
print(power_result1)
print("逐个元素的乘幂的结果2:")
print(power_result2)
运行结果:
逐个元素相加的结果1:
[[ 8 10 12]
[14 16 18]]
逐个元素相加的结果2:
[[ 8 10 12]
[14 16 18]]
逐个元素相减的结果1:
[[-6 -6 -6]
[-6 -6 -6]]
逐个元素相减的结果2:
[[-6 -6 -6]
[-6 -6 -6]]
逐个元素相乘的结果1:
[[ 7 16 27]
[40 55 72]]
逐个元素相乘的结果2:
[[ 7 16 27]
[40 55 72]]
逐个元素相除的结果1:
[[0.14285714 0.25 0.33333333]
[0.4 0.45454545 0.5 ]]
逐个元素相除的结果2:
[[0.14285714 0.25 0.33333333]
[0.4 0.45454545 0.5 ]]
逐个元素的乘幂的结果1:
[[ 1 256 19683]
[ 1048576 48828125 -2118184960]]
逐个元素的乘幂的结果2:
[[ 1 256 19683]
[ 1048576 48828125 -2118184960]]对于维数不同的矩阵,会先将维数较小者广播成与维数较大者具有相同维数的矩阵,再进行运算。
以加法为例:
import numpy as np
# 创建两个矩阵
matrix1 = np.array([[4, 5, 6]])
matrix2 = np.array([[7, 8, 9],
[10, 11, 12]])
# 逐个元素相加
add_result1 = np.add(matrix1, matrix2)
add_result2 = matrix1 + matrix2
print("逐个元素相加的结果1:")
print(add_result1)
print("逐个元素相加的结果2:")
print(add_result2)
运行结果:
逐个元素相加的结果1:
[[11 13 15]
[14 16 18]]
逐个元素相加的结果2:
[[11 13 15]
[14 16 18]]3.矩阵乘法
进行矩阵乘法运算,可以使用 NumPy 中的 np.dot() 函数或者 @ 运算符。
示例代码:
import numpy as np
# 创建两个矩阵
matrix1 = np.array([[1, 2, 3],
[4, 5, 6]])
matrix2 = np.array([[7, 8],
[9, 10],
[11, 12]])
# 使用 np.dot() 进行矩阵乘法
dot_result = np.dot(matrix1, matrix2)
print("矩阵乘法的结果:")
print(dot_result)
# 使用 @ 运算符进行矩阵乘法(Python 3.5+)
at_operator_result = matrix1 @ matrix2
print("使用 @ 运算符的结果:")
print(at_operator_result)
运行结果:
矩阵乘法的结果:
[[ 58 64]
[139 154]]
使用 @ 运算符的结果:
[[ 58 64]
[139 154]]7.矩阵运算与线性代数
Python中的线性代数运算主要使用 numpy.linalg 模块,常用函数如下:
| 函数 | 说明 |
| norm | 求向量或矩阵的范数 |
| inv | 求矩阵的逆阵 |
| pinv | 求矩阵的广义矩阵 |
| solve | 求解线性方程组 |
| det | 求矩阵的行列式 |
| lstsq | 最小二乘法求解超定线性方程组 |
| eig | 求矩阵的特征值和特征向量 |
| eigvals | 求矩阵的特征值 |
| svd | 矩阵的奇异值分解 |
| qr | 矩阵的QR分解 |
1.范数运算
np.linalg.norm() 函数用于计算向量或矩阵的范数。
调用格式:
np.linalg.norm(x, ord=None, axis=None, keepdims=False)
x:表示要计算范数的向量或矩阵。
ord:可选参数,表示计算范数的类型,默认为 None,表示计算 2 范数(默认的欧几里德范数)。常用的取值有:
None:默认值,表示计算 2 范数。
1:计算 1 范数(绝对值之和)。
2:计算 2 范数(默认的欧几里德范数)。
np.inf:计算无穷范数(绝对值的最大值)。
-np.inf:计算负无穷范数(绝对值的最小值)。
axis:可选参数,表示沿着哪个轴计算范数,默认为 None,表示对整个向量或矩阵计算范数。如果指定了 axis,则范数将沿着指定的轴计算。
keepdims:是否保持矩阵的二维特性,默认为False,即不保持。
示例代码:
import numpy as np
# 计算向量的 2 范数
vector = np.array([1, 2, 3])
norm_2 = np.linalg.norm(vector)
print("向量的 2 范数:", norm_2)
# 计算矩阵的 Frobenius 范数(2 范数)
matrix = np.array([[1, 2], [3, 4]])
frobenius_norm = np.linalg.norm(matrix)
print("矩阵的 Frobenius 范数:", frobenius_norm)
# 沿着指定轴计算矩阵的 1 范数
matrix = np.array([[1, 2, 3], [4, 5, 6]])
axis_1_norm = np.linalg.norm(matrix, ord=1, axis=0)
print("矩阵沿着轴 0 的 1 范数:", axis_1_norm)
运行结果:
向量的 2 范数: 3.7416573867739413
矩阵的 Frobenius 范数: 5.477225575051661
矩阵沿着轴 0 的 1 范数: [5. 7. 9.]2.求解线性方程组的唯一解
两种解法:
import numpy as np
a = np.array([[3, 1], [1, 2]])
b = np.array([9, 8])
# 第一种解法
x1 = np.linalg.inv(a) @ b
# 第二种解法
x2 = np.linalg.solve(a, b)
print(x1); print(x2)
运行结果:
[2. 3.]
[2. 3.]可知方程组的解为x=2,y=3。
3.求超定线性方程组的最小二乘解
示例代码:
import numpy as np
a = np.array([[3, 1], [1, 2], [1, 1]])
b = np.array([9, 8, 6])
x = np.linalg.pinv(a) @ b
print(np.round(x, 4))运行结果:
[2. 3.1667]可知方程组的解为x=2,y=3.1667。
补充:
round() 函数是 Python 内置的一个函数,用于对浮点数进行四舍五入。
调用格式:
round(number, ndigits=None)number:表示要进行四舍五入的数字。
ndigits:可选参数,表示保留的小数位数,默认为 None,表示不指定小数位数,直接对整数部分进行四舍五入。
2.SciPy
1.功能简介
SciPy 完善了 NumPy 的功能,提供了文件输入、输出功能,为多种应用提供了大量工具和算法,如基本函数、特殊函数、积分、优化、插值、傅里叶变换、信号处理、线性代数、稀疏特征值、稀疏图、数据结构、数理统计和多维图像处理等。
| 模块 | 功能 |
| scipy.cluster | 聚类分析等 |
| scipy.constants | 物理和数学常数 |
| scipy.fftpack | 傅里叶变换 |
| scipy.integrate | 积分 |
| scipy.interpolate | 插值 |
| scipy.io | 数据输入和输出 |
| scipy.linalg | 线性代数 |
| scipy.ndimage | n维图像 |
| scipy.odr | 正交距离回归 |
| scipy.optimize | 优化 |
| scipy.signal | 信号处理 |
| scipy.sparse | 稀疏矩阵 |
| scipy.spatial | 空间数据结构和算法 |
| scipy.special | 特殊函数 |
| scipy.stats | 统计 |
1.求解非线性方程(组)
利用 scipy.optimize 模块的 fsolve 和 root 求解。
调用格式:
scipy.optimize.fsolve(func, x0, args=(), ...)
scipy.optimize.root(fun, x0, args=(), method='hybr', ...)
共同参数说明:
func 或 fun:表示要求解的方程。
x0:表示方程的初始猜测值。
args:表示传递给 func 或 fun 的其他参数。
fsolve() 特有参数说明:
...:还可以接受其他参数,例如 xtol 和 full_output 等,用于控制求解过程的精度和输出结果。
root() 特有参数说明:
method:可选参数,表示要使用的求解方法。默认为 'hybr',表示使用混合法进行求解。
例1:求非线性方程的解
求方程![]() 在给定初值1.5附近的一个实根。
在给定初值1.5附近的一个实根。
示例代码:
from scipy.optimize import fsolve, root
fx = lambda x: x**980-5.01*x**979+7.398*x**978\
-3.388*x**977-x**3+5.01*x**2-7.398*x+3.388
x1 = fsolve(fx, 1.5, maxfev = 4000) # 函数调用4000次
x2 = root(fx, 1.5)
print(x1, '\n', '--------------------'); print(x2)
运行结果:
[1.21]
--------------------
fjac: array([[-1.]])
fun: array([-1.23341756e+69])
message: 'The solution converged.'
nfev: 319
qtf: array([2.00183544e+72])
r: array([2.54210657e+80])
status: 1
success: True
x: array([1.21])例2:求非线性方程组的解
示例代码:
from scipy.optimize import fsolve, root
fx = lambda x:[x[0]**2+x[1]**2-1, x[0]-x[1]]
s1 = fsolve(fx, [1, 1])
s2 = root(fx, [1, 1])
print(s1, '\n', '----------------'); print(s2)
运行结果:
[0.70710678 0.70710678]
----------------
fjac: array([[-0.81649679, -0.57734998],
[ 0.57734998, -0.81649679]])
fun: array([4.4408921e-16, 0.0000000e+00])
message: 'The solution converged.'
nfev: 9
qtf: array([-3.64625238e-10, 2.57828785e-10])
r: array([-1.73205167, -0.57735171, 1.63299357])
status: 1
success: True
x: array([0.70710678, 0.70710678])2.积分
1.对给定函数的数值积分
| 函数 | 说明 |
| quad(func, a, b, args) | 计算一重数值积分 |
| dblquad(func, a, b, gfun, hfun, args) | 计算二重数值积分 |
| tplquad(func, a, b, gfun, hfun, qfun, rfun) | 计算三重数值积分 |
| nquad(func, ranges, args) | 计算多变量积分 |
例:
分别计算 a = 2, b = 1; a = 2, b = 10,时,![]() 的值。
的值。
示例代码:
from scipy.integrate import quad
def fun46(x, a, b):
return a*x**2+b*x
I1 = quad(fun46, 0, 1, args = (2, 1))
I2 = quad(fun46, 0, 1, args = (2, 10))
print(I1); print(I2)
运行结果:
(1.1666666666666665, 1.2952601953960159e-14)
(5.666666666666667, 6.291263806209221e-14)
2.对给定离散点的数值积分
trapz()函数。
调用格式:
trapz(y, x=None, dx=1.0, axis=-1)
y:要进行积分的函数值数组。
x:可选参数,用于指定积分点的位置。如果未提供,则默认使用等间隔的点。
dx:可选参数,用于指定积分点之间的间距。默认值为1.0。
axis:可选参数,用于指定应用积分的轴。默认值为-1,表示在最后一个轴上进行积分。
返回值: 返回通过数值积分计算得到的结果。
代码示例:
import numpy as np
from scipy.integrate import trapz
# 创建离散点
x = np.linspace(0, 1, 100)
y = np.sin(x)
# 使用trapz函数进行数值积分
result = trapz(y, x)
print("数值积分结果:", result)
运行结果:
数值积分结果: 0.45969378553005223.最小二乘解
对于非线性方程组
其中x为m维向量,一般的,n>m,求方程组的最小二乘解即求![]() 的最小值。
的最小值。
scipy. optimize 模块求非线性方程组最小二乘解的函数调用格式:
from scipy. optimize import least squares
least squares(fun,x0)
其中 fun是定义向量函数![]() 的匿名函数的返回值,x0为x的初始值。
的匿名函数的返回值,x0为x的初始值。
例:
已知4个观测站的位置坐标![]() ,每个观测站都探测到距未知信号的距离
,每个观测站都探测到距未知信号的距离![]() ,已知数据见下表,试定位未知信号的位置坐标
,已知数据见下表,试定位未知信号的位置坐标![]() 。
。
| 站号 | 1 | 2 | 3 | 4 |
| 245 | 164 | 192 | 232 | |
| 442 | 480 | 281 | 300 | |
| 126.2204 | 120.7509 | 90.1854 | 101.4021 |
解:未知信号的位置坐标(x,y)满足非线性方程组:
该方程组是一个矛盾方程组,必须求最小二乘解。可以把问题转化为求多元函数
![]() 的最小点问题。
的最小点问题。
示例代码:
from scipy.optimize import least_squares
import numpy as np
a = np.loadtxt("data2_47.txt")
x0 = a[0]; y0 = a[1]; d = a[2]
fx = lambda x: np.sqrt((x0-x[0])**2+(y0-x[1])**2)-d
s = least_squares(fx, np.random.rand(2))
print(s, '\n', '----------------', '\n', s.x)运行结果:
active_mask: array([0., 0.])
cost: 0.3671505584636865
fun: array([-0.34333429, 0.13598942, -0.49656113, 0.59275341])
grad: array([-2.52489481e-08, 5.31418792e-09])
jac: array([[-0.75860568, -0.65155001],
[-0.11987284, -0.99278925],
[-0.4737608 , 0.88065357],
[-0.80877666, 0.58811592]])
message: '`ftol` termination condition is satisfied.'
nfev: 17
njev: 17
optimality: 2.524894809896594e-08
status: 2
success: True
x: array([149.50894333, 359.9847955 ])
----------------
[149.50894333 359.9847955 ]4.最大模特征值及对应的特征向量
例:
示例代码:
from scipy.sparse.linalg import eigs
import numpy as np
a = np.array([[1, 2, 3], [2, 1, 3], [3, 3, 6]], dtype = float) # 必须加 float,否则出错
b, c = np.linalg.eig(a)
d, e = eigs(a, 1)
print('最大模特征值为:', d)
print('对应的特征向量为:\n', e)运行结果:
最大模特征值为: [9.+0.j]
对应的特征向量为:
[[0.40824829+0.j]
[0.40824829+0.j]
[0.81649658+0.j]]补充:j表示复数。
3.SymPy
1.功能简介
SymPy 符号运算库能够解简单的线性方程、非线性方程及简单的代数方程组。
2.定义符号变量或符号函数
1.使用symbols()函数
import sympy as sp
x, y, z = sp.symbols('x, y, z') # 或 x, y, z = sp.symbols('x y z')
f, g = sp.symbols('f, g', cls = sp.Function) # 定义多个符号函数
y = sp.Function('y') # 定义符号函数2.使用var()函数
import sympy as sp
sp.var('x, y, z')
sp.var('a b c') # 中间分隔符更换为空格
sp.var('f, g', cls = sp.Function) # 定义符号函数3.求解符号代数方程(组)
例1:
利用 solve 求符号代数方程![]() 的解。
的解。
示例代码:
import sympy as sp
a, b, c, x = sp.symbols('a, b, c, x')
x0 = sp.solve(a*x**2+b*x+c, x)
print(x0)运行结果:
[(-b - sqrt(-4*a*c + b**2))/(2*a), (-b + sqrt(-4*a*c + b**2))/(2*a)]例2:
求方程组的符号解。
示例代码一:
import sympy as sp
sp.var('x1, x2')
s = sp.solve([x1**2+x2**2-1, x1-x2], [x1, x2])
print(s)运行结果:
[(-sqrt(2)/2, -sqrt(2)/2), (sqrt(2)/2, sqrt(2)/2)]示例代码二:
import sympy as sp
x = sp.var('x:2') # 定义符号数组
s = sp.solve([x[0]**2+x[1]**2-1, x[0]-x[1]], x)
print(s)运行结果:
[(-sqrt(2)/2, -sqrt(2)/2), (sqrt(2)/2, sqrt(2)/2)]4.Pandas
1.功能简介
Pandas 工具库能处理 NumPy 和 SciPy 所不能处理的问题。由于其特有的数据结构, Pandas 可以处理包含不同类型数据的复杂表格(这是 NumPy 数组无法做到的)和时间序列。 Pandas 可以轻松又顺利地加载各种形式的数据。然后,可随意对数据进行切片、切块、处理缺失元素、添加、重命名、聚合、整形和可视化等操作。
通常, Pandas 库的导入名称为 pd :
import pandas as pd2.Pandas基本操作
Pandas主要提供了三种数据结构:
(1)Series:带标签的一维数据。
(2)DataFrame:带标签且大小可变的二维表格结构。
(3)Panel:带标签且大小可变的三维数组。
主要介绍DataFrame数据结构。
1.生成二维数组
例:
生成服从标准正态分布的 24*4 随机数矩阵,并保存为DataFrame。
import pandas as pd
import numpy as np
dates = pd.date_range(start = '20191101', end = '20191124', freq = 'D')
a1 = pd.DataFrame(np.random.randn(24, 4), index = dates, columns = list('ABCD'))
a2 = pd.DataFrame(np.random.rand(24, 4))2.读写文件
不熟悉文件基本操作的读者可以先阅读这篇博文:
http://t.csdnimg.cn/6Ljb6
1.数据写入文件
# 包含行索引
import pandas as pd
import numpy as np
dates = pd.date_range(start = '20191101', end = '20191124', freq = 'D')
a1 = pd.DataFrame(np.random.randn(24, 4), index = dates, columns = list('ABCD'))
a2 = pd.DataFrame(np.random.randn(24, 4))
a1.to_excel('data2_38_1.xlsx')
a2.to_csv('data2_38_2.csv')
f = pd.ExcelWriter('data2_38_3.xlsx') # 创建文件对象
a1.to_excel(f, "Sheet1") # 把 a1 写入excel文件
a2.to_excel(f, "Sheet2") # 把 a2 写入另一个表单中
f.save()# 不包含行索引
import pandas as pd
import numpy as np
dates = pd.date_range(start = '20191101', end = '20191124', freq = 'D')
a1 = pd.DataFrame(np.random.randn(24, 4), index = dates, columns = list('ABCD'))
a2 = pd.DataFrame(np.random.randn(24, 4))
a1.to_excel('data2_38_4.xlsx', index=False)
a2.to_csv('data2_38_5.csv', index=False)
f = pd.ExcelWriter('data2_38_6.xlsx') # 创建文件对象
a1.to_excel(f, "Sheet1", index=False) # 把 a1 写入excel文件
a2.to_excel(f, "Sheet2", index=False) # 把 a2 写入另一个表单中
f.save()2.从文件中读入数据
import pandas as pd
a = pd.read_csv('data2_38_2.csv', usecols = range(1, 5))
b = pd.read_excel('data2_38_3.xlsx', "Sheet2", usecols = range(1, 5))
3.数据的预处理
1.拆分、合并和分组计算
在进行数据处理和分析时,经常需要按照某一列对原始数据进行分组,而该列数值相同的行中其他列进行求和、求平均等操作,这可以通过 groupby ()方法、 sum ()方法和 mean ()方法等来实现。
import pandas as pd
import numpy as np
d = pd.DataFrame(np.random.randint(1, 6, (10, 4)), columns = list('ABCD'))
d1 = d[:4] # 获取前 4 行数据
d2 = d[4:] # 获取第 5 行以后的数据
dd = pd.concat([d1, d2]) # 数据行合并
s1 = d.groupby('A').mean() # 数据分组求均值
s2 = d.groupby('A').apply(sum) # 数据分组求和2.数据的选取与清洗
对DataFrame进行选取,要从3个层次考虑:行列、区域、单元格。
(1)选用中括号[]选取行列。
(2)使用行和列的名称进行标签定位的df. loc[]。
(3)使用整型索引(绝对位置索引)的df iloc[]。
在数据预处理中,需要对缺失值等进行一些特殊处理。
import pandas as pa
import numpy as np
a = pd.DataFrame(np.random.randint(1, 6, (5, 3)),
index = ['a', 'b', 'c', 'd', 'e'],
columns = ['one', 'two', 'three'])
a.loc['a', 'one'] = np.nan # 修改第 1 行第 1 列的数据
b = a.iloc[1:3, 0:2].values # 提取第 2、3 行,第 1、2 列数据
a['four'] = 'bar' # 增加第 4 列数据
a2 = a.reindex(['a', 'b', 'c', 'd', 'e', 'f'])
a3 = a2.dropna() # 删除有不确定值的行5.Matplotlib
1.功能简介
Matplotlib 是一个包含各种绘图模块的库,能根据数组创建高质量的图形,并交互式地显示它们。Matplotlib 提供了 pylab 接口, pylab 包含许多像 MATLAB 一样的绘图组件。使用如下命令,可以轻松导入可视化所需要的模块:
import matplotlib.pyplot as plt 或者
import pylab as plt2.二维绘图
1.折线图和柱状图
使用matplotlib.pyplot模块的plot函数画折线图。
调用格式一:
plot(x, y, s)x, y 为数据点的坐标,s 为 指定线条颜色、线条样式和数据点形状的字符串。
| 符号参数 | 类型 | 含义 |
| b | 线条颜色 | 蓝色 |
| c | 青色(cyan) | |
| g | 绿色 | |
| k | 黑色 | |
| m | 品红(magenta) | |
| r | 红色 | |
| w | 白色 | |
| y | 黄色 | |
| - | 线条样式 | 实线 |
| -- | 虚线 | |
| -. | 点划线 | |
| : | 点线 | |
| . | 数据点形状 | 点 |
| o | 圆圈 | |
| * | 星形 | |
| x | 十字架 | |
| s | 正方形 | |
| p | 五角星 | |
| D/d | 钻石/小钻石 | |
| h | 六角形 | |
| + | 加号 | |
| | | 竖直线 | |
| V^<> | 下(上、左、右)三角形 | |
| 1234 | Tripod 向下(上、左、右) |
调用格式二:
plot(x, y, linestyle, linewidth, color, marker, markersize, markeredgecolor, markerfacecolor, markeredgewidth, label, alpha)linestyle:指定折线的类型,可以是实线、虚线和点画线等,默认为实线。linewidth:指定折线的宽度。
marker:可以为折线图添加点,该参数设置点的形状。
markersize:设置点的大小。
markeredgecolor:设置点的边框色。
markerfacecolor:设置点的填充色。
markeredgewidth :设置点的边框宽度。
label :添加折线图的标签,类似于图例的作用。
alpha :设置图形的透明度。
例:
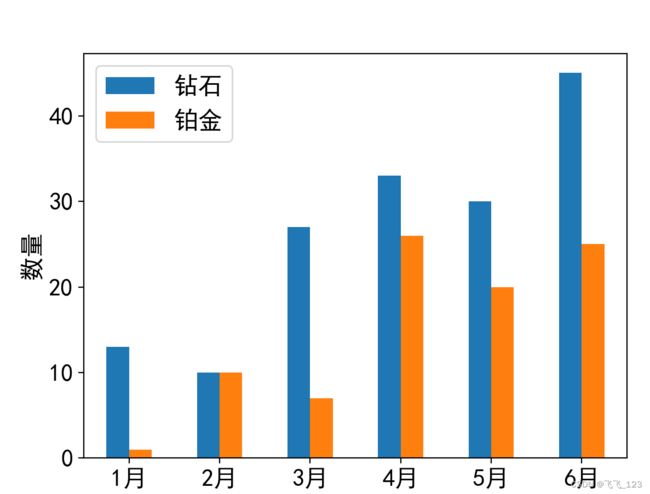
已知某店铺商品的销售量如下表所列,画出商品销售趋势图。
| 月份 | 1 | 2 | 3 | 4 | 5 | 6 |
| 钻石销量/个 | 13 | 10 | 27 | 33 | 30 | 45 |
| 铂金销量/只 | 1 | 10 | 7 | 26 | 20 | 25 |
折线图:
import pandas as pd
import matplotlib.pylab as plt
plt.rc('font', family='SimHei') # 用来正常显示中文标签
plt.rc('font', size=16) # 设置显示字体大小
a = pd.read_excel("data.xlsx", header=None, engine="openpyxl")
b = a.values
x = b[0, 1:]
y = b[1:, 1:]
plt.plot(x, y[0], '-*b', label='钻石')
plt.plot(x, y[1], '--dr', label='铂金')
plt.xlabel('月份')
plt.ylabel('每月销量')
plt.legend(loc='upper left')
plt.grid()
plt.show()
运行结果:
需要注意的是在上述代码中,read_excel()函数读取的Excel文件内容如下:
原书的Excel文件中应该是没有第一列的,否则按照原书中的代码:
plt.plot(x, y[0], '-*b', label='钻石')
plt.plot(x, y[1], '--dr', label='铂金')运行结果会报错:
TypeError: 'value' must be an instance of str or bytes, not a int这个错误误导性很强,实际上错误的引用不是因为二维数组 y 中的元素是 int 类型,而是因为表格的第一列数据是错误的坐标值,用切片操作将其去除即可。
2.Pandas结合Matplotlib进行数据可视化
接续上面的例子,画出销售数据的柱状图。
示例代码:
import pandas as pd
import pylab as plt
plt.rc('font', family='SimHei')
plt.rc('font', size=16)
a = pd.read_excel('data.xlsx', header=None)
# 删除第一列
a = a.drop(a.columns[0], axis=1)
# 保存修改后的Excel文件到新的文件
a.to_excel('modified_data.xlsx', index=False)
b = a.T
b.plot(kind='bar')
plt.legend(['钻石', '铂金'])
plt.xticks(range(6), b[0], rotation=0)
plt.ylabel('数量')
plt.show()
运行结果:
此处同样存在需要删除第一列的问题,但操作对象是Excel文件,而不是数组,不能用切片操作。可以直接在Excel文件中删除,但最好能掌握用Python命令删除Excel中的一列数据的方法。注意修改后的Excel不能保存到原文件,否则文件会锁定,导致没有权限读取。
3.子图
例:
把一个窗口分成 3 个子窗口,分别绘制如下三个子图:
(1)柱状图;
(2)饼图;
(3)曲线![]() 。
。
示例代码:
import pylab as plt
import numpy as np
plt.rc('text', usetex=True) # 调用字库
y1 = np.random.randint(2, 5, 6)
y1 = y1/sum(y1)
plt.subplot(2, 2, 1)
string = ['apple', 'grape', 'peach', 'pear', 'banana', 'pineapple']
plt.barh(string, y1) # 水平条形图
plt.subplot(222)
plt.pie(y1, labels=string) # 饼图
plt.subplot(212)
x2 = np.linspace(0.01, 10, 100)
y2 = np.sin(10*x2)/x2
plt.plot(x2, y2)
plt.xlabel('$x$')
plt.ylabel('$\\mathrm{sin}(10x)/x$')
plt.show()
运行结果:
注意把原书代码中的 str 改成 string 或其他变量名,不要用关键字作变量名。
3.三维绘图
1.三维曲线
例:
画出三维曲线 ![]() 的图形。
的图形。
示例代码:
import pylab as plt
import numpy as np
plt.rcParams['axes.unicode_minus']=False
ax = plt.axes(projection='3d')
z = np.linspace(-50, 50, 1000)
x = z**2*np.sin(z)
y = z**2*np.cos(z)
ax.plot(x, y, z, 'k')
plt.show()运行结果:
这次运行地很顺利,没有出什么 bug !
2.三维曲面图
例:
画出三维曲面![]() 。
。
示例代码:
import pylab as plt
import numpy as np
x = np.linspace(-4, 4, 100)
x, y = np.meshgrid(x, x)
z = 50*np.sin(x+y)
ax = plt.axes(projection='3d')
ax.plot_surface(x, y, z, color='y')
plt.show()
运行结果:
很好看有木有,并不比MATLAB差!
6.IPython
1.功能简介
IPython 满足了 Python 交互式 shell 命令的需要,它是基于 shell 、Web 浏览器和应用程序接口的 Python 版本,具有图形化集成、自定义指令、丰富的历史记录和并行计算等增强功能。它通过脚本、数据和相应结果清晰又有效地说明了各种操作。
IPython 在数学建模中作用不大,在此不详细说明。
7.参考文献
【1】《Python数学建模算法与应用》
【2】《Python基础教程(第2版)》