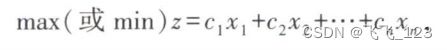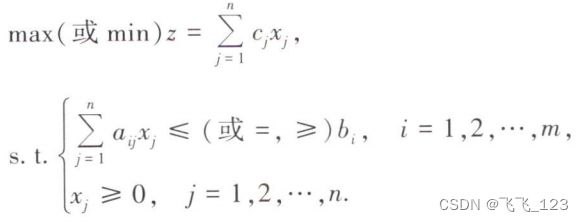Python数学建模之线性规划和整数规划模型

1.线性规划模型

1.线性规划模型及概念

1.求解线性规划模型的一般步骤：

2.线性规划模型的一般形式

或简写为：

 

3.向量形式

4.矩阵形式

 5.线性规划问题的解

2.模型求解及应用

需要用Python的cvxpy库。安装步骤参见http://t.csdnimg.cn/ONvge

例1：

 代码示例：

import cvxpy as cp
from numpy import array
c = array([70, 50, 60])                      # 定义目标向量
a = array([[2, 4, 3],[3, 1, 5], [7, 3, 5]])  # 定义约束矩阵
b = array([150, 160, 200])                   # 定义约束条件的右边向量
x = cp.Variable(3, pos=True)                 # 定义 3 个决策变量
obj = cp.Maximize(c@x)                       # 构造目标函数
cons = [a@x<=b]                              # 构造约束条件
prob = cp.Problem(obj, cons)
prob.solve(solver='GLPK_MI')                 # 求解问题
print('最优解为：', x.value)
print('最优值为：', prob.value)

例2：

示例代码： 

import cvxpy as cp
x = cp.Variable((5, 4), pos=True)
obj = cp.Maximize(1.15*x[3, 0]+1.40*x[1, 2]+1.25*x[2, 1]+1.06*x[4, 3])
cons = [x[0, 0]+x[0, 3] == 100000,
       x[1, 0]+x[1, 2]+x[1, 3] == 1.06*x[0, 3],
       x[2, 0]+x[2, 1]+x[2, 3] == 1.15*x[0, 0]+1.06*x[1, 3],
       x[3, 0]+x[3, 3] == 1.15*x[1, 0]+1.06*x[2, 3],
       x[4, 3] == 1.15*x[2, 0]+1.06*x[3, 3],
       x[2, 1]<=40000,x[1,2]<=30000]
prob = cp.Problem(obj, cons)
prob.solve(solver='GLPK_MI')
print('最优解为：', x.value)
print('最优值为：', prob.value)

例3：

示例代码：

import cvxpy as cp
x = cp.Variable((4, 4), pos=True)
obj = cp.Minimize(2800*sum(x[:,0])+4500*sum(x[:3,1])+6000*sum(x[:2,2])+7300*x[0,3])
cons = [sum(x[1,:])>=15,
       sum(x[0,1:])+sum(x[2,:3])>=10,
       sum(x[0,2:])+sum(x[1,1:3])+sum(x[2,:2])>=20,
       x[0,3]+x[1,2]+x[2,1]+x[3,0]>=12]
prob = cp.Problem(obj, cons)
prob.solve(solver='GLPK_MI')
print('最优解为：\n',x.value)
print('最优值为：',prob.value)

例4：

示例代码：

import numpy as np
import cvxpy as cp
import pandas as pd
c = np.genfromtxt('data4_5_1.txt', dtype=float, max_rows=6, usecols=range(8)) # 读前 6 行前 8 列数据
e = np.genfromtxt('data4_5_1.txt', dtype=float, max_rows=6, usecols=8)        # 读最后一列数据
d = np.genfromtxt('data4_5_1.txt', dtype=float, skip_header=6)                # 读最后一行数据
x = cp.Variable((6, 8), pos=True)
obj = cp.Minimize(cp.sum(cp.multiply(c, x)))
con = [cp.sum(x,axis=0)==d,
      cp.sum(x,axis=1)<=e]
prob = cp.Problem(obj, con)
prob.solve(solver='GLPK_MI')
print('最优解为：\n', x.value)
print('最优值为：', prob.value)
xd = pd.DataFrame(x.value)
xd.to_excel('data4_5_2.xlsx')                                                 # 数据写到 excel 文件，便于做表使用
 
# 通过 excel 文件传递数据
# 程序文件 ex4_5_2.py
import cvxpy as cp
import pandas as pd
data = pd.read_excel('data4_5_3.xlsx', header=None)
data = data.values
c = data[:-1, :-1]
d = data[-1, :-1]
e = data[:-1, -1]
x = cp.Variable((6, 8), pos=True)
obj = cp.Minimize(cp.sum(cp.multiply(c, x)))
con = [cp.sum(x,axis=0)==d,
      cp.sum(x,axis=1)<=e]
prob = cp.Problem(obj, con)
prob.solve(solver='GLPK_MI')
print('最优解为：\n', x.value)
print('最优值为：', prob.value)
xd = pd.DataFrame(x.value)
xd.to_excel('data4_5_4.xlsx')

2.整数规划

1.整数线性规划模型

 

2.整数线性规划模型的求解

例1：纯整数规划

import cvxpy as cp
x = cp.Variable(6, integer=True)
obj = cp.Minimize(sum(x))
cons = [x[0]+x[5]>=35,x[0]+x[1]>=40,
       x[1]+x[2]>=50,x[2]+x[3]>=45,
       x[3]+x[4]>=55,x[4]+x[5]>=30,
       x>=0]
prob = cp.Problem(obj, cons)
prob.solve(solver='GLPK_MI')
print('最优值为：', prob.value)
print('最优解为：', x.value)
 
# 解法二：求余运算
import cvxpy as cp
import numpy as np
a = np.array([35, 40, 50, 45, 55, 30])
x = cp.Variable(6, integer=True)
obj = cp.Minimize(sum(x))
cons = [x>=0]
for i in range(6):
    cons.append(x[(i-1)%6]+x[i]>=a[i])
prob = cp.Problem(obj, cons)
prob.solve(solver='GLPK_MI')
print('最优值为：', prob.value)
print('最优解为：', x.value)

 例2：0-1整数规划

import cvxpy as cp
import numpy as np
c = np.loadtxt('data4_10.txt')
x = cp.Variable((4, 5), integer=True)           # 定义决策变量
obj = cp.Minimize(cp.sum(cp.multiply(c, x)))    # 构造目标函数
cons = [0<=x, x<=1, cp.sum(x, axis=0)==1,       # 构造约束条件
        cp.sum(x, axis=1)<=2]
prob = cp.Problem(obj, cons)
prob.solve(solver='GLPK_MI')                    # 求解问题
print('最优解为：\n', x.value)
print('最优值为：', prob.value)

例3:0-1整数规划 

import cvxpy as cp
import numpy as np
a = np.loadtxt('data4_11.txt')
d = np.zeros((10, 10))
for i in range(10):
    for j in range(10):
        d[i, j] = np.linalg.norm(a[:, i]-a[:, j])
x = cp.Variable(10, integer=True)
y = cp.Variable((10, 10), integer=True)
obj = cp.Minimize(sum(x))
cons = [sum(y)>=1, cp.sum(y, axis=1)<=5,
        x>=0, x<=1, y>=0, y<=1]
for i in range(10):
    cons.append(x[i]==y[i, j])
    for j in range(10):
        cons.append(d[i, j]*y[i, j]<=10*x[i])
        cons.append(x[i]>=y[i, j])
prob = cp.Problem(obj, cons)
prob.solve(solver='GLPK_MI')
print('最优值为：', prob.value)
print('最优解为：\n', x.value)
print('----------\n', y.value)