最大流—EK算法，流网络，残留网络，定理证明，详细代码

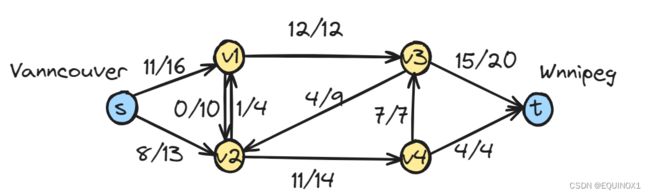
零、卡车运输

Lucky Puck公司有冰球工厂Vancouver，即源点s，Winnipeg仓库是汇点t，冰球由卡车装载经由中间城市运送，但是每天只能有c(u , v)箱从城市u运送到城市v，在图上表示，每条边有上有 f / c数字表示，f为沿这条有向边的运输冰球的箱数，c即为c(u,v)，每天都有p箱冰球从Vancouver出发，p箱冰球到达Winnipeg。

作为公司老板的Puck，应该如何规划每条道路上的运载量才能使得每天从冰球工厂发出的冰球箱数p最大呢？

---

一、流网络

1.1流网络

流网络G = (V , E)是一个有向图，其中每条边(u , v)∈E均有一非负容量c(u , v) ≥ 0。如果(u , v) ∉ E，则c(u , v) = 0。

流网络中有两个特别的点：源点s和汇点t。如例中的工厂和仓库。

1.2流

设f(x , y)是定义在节点二元组(x∈V , y∈V)上的实数函数，且满足：

1. $$容量限制:f(x,y)\le c(x,y)$$

2. $$反对称性:f(x,y)=-f(y,x)$$

3. $$流守恒性:\forall x\ne s,x\ne t,\sum _{(u,x)\in E}f(u,x)=\sum _{(x,v)\in E}f(x,v)$$

f(x,y)称为流网络的流函数 , 对于(x , y)∈E , f(x , y)称为边的流量 , c(x , y) - f(x , y)称为边的剩余流量.

流 f 值的定义为
$$\left|f\right|=\sum _{v\in V}f(s,v)$$
亦即 , 从源点s发出的总流。如例中每天从工厂发出的冰球的箱数。

1.3最大流

对于一个给定的流网络 , 合法的流函数 f 有很多. 使得流的值最大的流函数被称为网络的最大流 , 此时的流的值被称为网络的最大流量.

1.4残留网络

假定有一个流网络G = (V , E)，其源点为s，汇点为t。设f为G中的一个流，一对顶点u, v∈V。在不超过容量c(u，v)的条件下，从u到v之间可以压入的额外网络流量，就是**(u，v) 的残留容量(residual capacity)**，由下式定义:
$$c_f(u,v)=c(u,v)-f(u,v)$$

给定一流网络G = (V , E)和流f，由f压得的G的残留网络是Gf = (V , Ef)，其中：
$$E_f=\{(u,v)\in V\times V:c_f(u,v)>0\}$$
即，残留网络包含了流网络的所有点，和残留容量大于0的有向边。

注意Ef中的边既可以是E中的有向边也可以是其反向边，若(u , v)∈E，有f(u , v) < c(u , v)，那么根据流网络的性质可知f(v , u) = -f(u,v)，那么对应残留容量就是c(v , u) - (-f(u,v)) = c(v , u) + f(u , v) > 0，则其反向边也在残留网络中。

由残留网络可以得出引理：

f 为G中的一个流，f‘为Gf中的一个流，那么f + f’仍为流网络G的一个流，其流量为| f + f’ | = | f | + | f‘ |

具体证明可以自己尝试或见《算法导论》

1.5增广路径

已知流网络G = (V , E)和流f，增广路径p为残留网络Gf中由源点s到汇点t的一条简单路径。

根据残留网络的定义，增广路径上的每条边的剩余容量都大于0，则该路径上的每条边都可以额外容纳一定的流量，这也和我们后续求最大流密切相关。

不难想出，增广路径可以增加的最大流量为该路径上边的最小残留容量。

1.6流网络的割

流网络G = (V , E)的割(S , T)将V划分为S和T两部分，使得s∈S，t属于T，通过割的流量为S和T之间边上流量的代数和，但是割的容量仅包含从S到T的边的容量的代数和。

如下图，割(S,T)的流量f(S,T) = 12 - 4 + 11 = 19

容量c(S,T) = 12 + 14 = 26

我们称容量最小的割为最小割。

可以证明f(S , T) = | f | ≤ c(S, T)（证明见《算法导论》）

1.7最大流最小割定理

如果 f是具有源点s和汇点t的流网络G = (V , E)中的一个流，那么下列条件是等价的：

1. f是G的一个最大流
2. 残留网络Gf不包含增广路
3. 存在G的某个割(S , T)，有| f | = c(S , T)

1.7.1证明

采用循环证明法，(1) => (2) , (2) => (3) , (3) => (1)

(1) => (2):

很容易证明，采用反证法即可

假设Gf含增广路，那么我们可以在Gf中构造一流f’，| f‘ | = min(cf(u,v) , (u , v) ∈ Ef)，那么f + f’仍为流网络的一个流（由1.4中介绍的引理可知），那么|f + f‘| > | f |，那么f就不是最大流，矛盾，则(1) => (2)成立

(2) => (1):

我们只需要在(2)的条件下构造出一个满足(3)的割即可。

选取集合S = {v ∈ V：Gf中从s到v存在一条通路}，T = V - S，划分(S , T)为一个割。

对所有，u∈S，v∈T，f(u , v) = c(u , v)，否则v就属于S。

由此推出| f | = f(S , T) = c(S , T)

(3) => (1):

也很容易证明，由于由于| f | ≤ c(S, T)，而此时| f | = c(S , T)，故不存在比f更大的流，故f为最大流。

1.8Ford-Fulkerson方法

Ford-Fulkerson方法是最大流的经典求解方法，之所以称之为”方法“而非”算法“，是由于它包含具有不同运行时间的几种实现。

Ford-Fulkerson方法依赖于三种重要思想：残留网络(residual network)、增广路(augmenting path)和割(cut)。这些思想是最大流最小割定理的精髓，这里给出Ford-Fulkerson方法的特定实现。

伪代码如下：

Ford-Fulkerson(G , s , t)
初始化流f = 0
while 流网络中存在增广路p
	do 沿着p增加f
return f

二、Edmonds-Karp算法

2.1定义

Ford-Fulkerson方法的第三行寻找p的过程，采用bfs来计算，这种实现方法即Edmonds-Karp算法。

算法原理已经不需要介绍了，即最大流最小割定理，不同算法只是Ford-Fulkerson方法的不同实现，我们直接给出EK算法的实现。

2.2EK算法的实现

• 建图，建立的有向边，初始容量为w，同时建立的反向边，初始容量为0，最大流maxflow = 0
• 路径数组pre记录增广路上点的前驱边，数组incf存储每条边的剩余容量，标记数组vis用于记录点是否访问
• bfs找增广路
  • 初始，源点s进入队列q，vis[s] = 1
  • 从队头取出u，遍历u发出的边i，incf[v] = min(w(i) , incf[u])，v入队，pre[v] = i
  • 如果u = t，说明找到增广路，return true
  • 否则队空，return false
• 找到增广路，maxflow += incf[t] , 从t开始向前更新剩余容量，w(pre[x]) = incf[x]
• 没找到增广路，说明最大流计算完毕，返回maxflow

2.3EK算法详细代码

采用链式前向星存图，每条边和其反向边的编号间的关系为异或1关系

关于链式前向星详见：一种实用的边的存储结构–链式前向星-CSDN博客

#define N 205
#define M 5005
const int MOD = 10000007;
const int inf = 0x3f3f3f3f3f3f3f3f;

struct edge
{
    int v, w, nxt;
} edges[M << 1];
int head[N], idx = 0;
inline void addedge(int u, int v, int w)
{
    edges[idx] = {v, w, head[u]};
    head[u] = idx++;
}

int n, m, s, t, incf[N], pre[N];
bool vis[N];

bool bfs()
{
    memset(vis, 0, sizeof(vis));
    queue q;
    q.emplace(s), vis[s] = true, incf[s] = inf;
    while (q.size())
    {
        int u = q.front();
        q.pop();
        for (int i = head[u]; ~i; i = edges[i].nxt)
        {
            int v = edges[i].v;
            if (!vis[v] && edges[i].w)
            {
                vis[v] = 1;
                incf[v] = min(incf[u], edges[i].w);
                pre[v] = i, q.emplace(v);
                if (v == t)
                    return true;
            }
        }
    }
    return false;
}

int EK()
{
    int maxflow = 0;
    while (bfs())//找增广路
    {
        int x = t;
        while (x != s)//更新剩余容量
        {
            int i = pre[x];
            edges[i].w -= incf[t];
            edges[i ^ 1].w += incf[t];
            x = edges[i ^ 1].v;
        }
        maxflow += incf[t];
    }
    return maxflow;
}

//main
    int a, b, c;
    memset(head, -1, sizeof(head));
    cin >> n >> m >> s >> t;
    for (int i = 0; i < m; i++)
        cin >> a >> b >> c, addedge(a, b, c), addedge(b, a, 0);
    cout << EK();

2.4OJ练习

P3376 【模板】网络最大流 - 洛谷 | 计算机科学教育新生态 (luogu.com.cn)

板子题，直接跑板子即可

#define _CRT_SECURE_NO_WARNINGS
#include 
#include 
#include 
#include 
#include 
#include 
using namespace std;
#define sc scanf
#define int long long
#define N 205
#define M 5005
const int MOD = 10000007;
const int inf = 0x3f3f3f3f3f3f3f3f;

struct edge
{
    int v, w, nxt;
} edges[M << 1];
int head[N], idx = 0;
inline void addedge(int u, int v, int w)
{
    edges[idx] = {v, w, head[u]};
    head[u] = idx++;
}

int n, m, s, t, incf[N], pre[N];
bool vis[N];

bool bfs()
{
    memset(vis, 0, sizeof(vis));
    queue q;
    q.emplace(s), vis[s] = true, incf[s] = inf;
    while (q.size())
    {
        int u = q.front();
        q.pop();
        for (int i = head[u]; ~i; i = edges[i].nxt)
        {
            int v = edges[i].v;
            if (!vis[v] && edges[i].w)
            {
                vis[v] = 1;
                incf[v] = min(incf[u], edges[i].w);
                pre[v] = i, q.emplace(v);
                if (v == t)
                    return true;
            }
        }
    }
    return false;
}

int EK()
{
    int maxflow = 0;
    while (bfs())
    {
        int x = t;
        while (x != s)
        {
            int i = pre[x];
            edges[i].w -= incf[t];
            edges[i ^ 1].w += incf[t];
            x = edges[i ^ 1].v;
        }
        maxflow += incf[t];
    }
    return maxflow;
}

void solve()
{
    int a, b, c;
    memset(head, -1, sizeof(head));
    cin >> n >> m >> s >> t;
    for (int i = 0; i < m; i++)
        cin >> a >> b >> c, addedge(a, b, c), addedge(b, a, 0);
    cout << EK();
}

signed main()
{
    ios::sync_with_stdio(false);
    cin.tie(0), cout.tie(0);
    freopen("in.txt", "r", stdin);
    int _ = 1;
    // cin >> _;
    while (_--)
        solve();
}