代码随想录算法训练营第23天 | 669. 修剪二叉搜索树 108.将有序数组转换为二叉搜索树 538.把二叉搜索树转换为累加树

修剪二叉搜索树

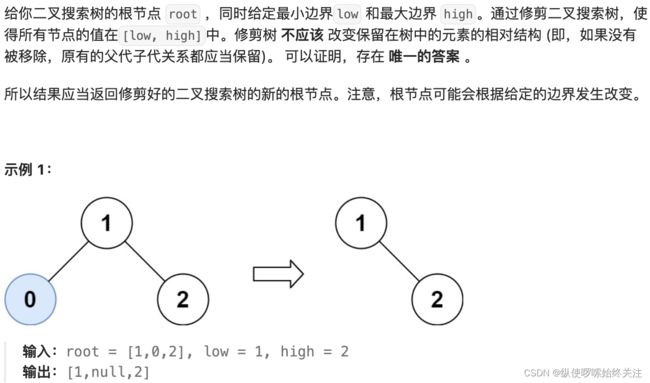
这道题感觉有点难理解，需要反复看。难点在于我们不能单单找到小于 low 或大于 high 的节点就删除整个子树，还需要关注该节点的右子树是不是还有符合的节点。

class Solution{
public:
	TreeNode* trimBST(TreeNode* root, int low, int high){
		if(root == NULL)  return root;
		if(root->val < low){  // 当前节点小于low，进一步查看右子树，返回符合条件的节点
			return trimBST(root->right, low, high);
		}
		if(root->val > high){
			return trimBST(root->left, low, high);
		}
		root->left = trimBST(root->left, low, high);  // 接入符合条件的左孩子
		root->right = trimBST(root->right, low, high);
		return root;
	}
};

迭代法，仍然是要注意不能单单因为当前节点不符合条件就扔掉整个子树，仍需要遍历它的左子树或者右子树来寻找符合条件的节点。也不能因为当前的节点符合条件就不处理子树，需要遍历左子树或者右子树来寻找不符合条件的节点。

class Solution{
public:
	TreeNode* trimBST(TreeNode* root, int low, int high){
		// 先处理头部节点，使根节点符合[L,R]区间的条件
		while(root && (root->val < low || root->val > high)){
			if(root->val < low)  root = root->right;
			else  root = root->left;
		}
		TreeNode* cur = root;
		while(cur){  // 通过更改cur的左节点来删除小于low的节点
			while(cur->left && cur->left->val < low){  
				// 用更大的右节点替代原来的左节点，使左节点的值>=L
				cur->left = cur->left->right;
			}
			cur = cur->left;  // 更新cur节点，查看左子树中是否还有不符合条件的节点
		}
		cur = root;
		while(cur){
			while(cur->right && cur->right->val > high){
				cur->right = cur->right->left;
			}
			cur = cur->right;
		}
		return root;
	}
};

将有序数组转换为二叉搜索树

这道题和最大二叉树和通过中序后序序列构造二叉树两道题是很相似的。关键点是递归寻找中间节点作为根节点。

class Solution{
public:
	TreeNode* traversal(vector<int>& nums, int left, int right){
		if(left > right)  return NULL;
		int mid = left + (right - left) / 2;
		TreeNode* root = new TreeNode(nums[mid]);  // 构造平衡树，所以取靠中间的数组元素作为根节点
		root->left = traversal(nums, left, mid - 1);
		root->right = traversal(nums, mid + 1, right);
		return root;
	}
	TreeNode* sortedArrayToBST(vector<int>& nums){
		return traversal(nums, 0, nums,size());
	}
};

迭代法，使用三个队列来模拟上述过程，一个存遍历节点，一个存左端点，一个存右端点。

class Solution{
public:
	TreeNode* sortedArrayToBST(vector<int>& nums){
		if(nums.size() == 0)  return nullptr;
		stack<TreeNode*> stNode;
		stack<int> stLeft;
		stack<int> stRight;
		TreeNode* root = new TreeNode();
		stNode.push(root);
		stLeft.push(0);
		stRight.push(nums.size() - 1);
		while(!stNode.empty()){
			TreeNode* node = stNode.top();
			stNode.pop();
			int left = stLeft.top();
			stLeft.pop();
			int right = stRight.top();
			stRight.pop();
			int mid = left + (right - left) / 2;
			node->val = nums[mid];
			if(left <= mid - 1){
				node->left = new TreeNode();
				stNode.push(node->left);
				stLeft.push(left);
				stRight.push(mid - 1);
			}
			if(right >= mid + 1){
				node->right = new TreeNode();
				stNode.push(node->right);
				stLeft.push(mid + 1);
				stRight.push(right);
			}
		}
		return root;
	}
};

把二叉搜索树转换为累加树

二叉搜索树是有序的，这道题所说的累加树应该是从大到小进行加和，因此需要反中序遍历。

class Solution{
public:
	int pre = 0;
	void traversal(TreeNode* node){
		if(!node)  return;
		traversal(node->right);
		node->val += pre;
		pre = node->val;
		traversal(node->left);
	}
	TreeNode* convertBST(TreeNode* root){
		if(!root)  return nullptr;
		traversal(root);
		return root;
	}
};