优先级队列以及堆

一.概念

队列是一种先进先出的数据结构，但有些情况下，操作的数据可能有优先级，一般出队列时，优先级高的先出，这种数据结构就是优先级队列：PriorityQueue。

PriorityQueue的底层使用了堆这种数据结构，而堆的本质其实就是完全二叉树

二.堆

概念

堆其实就是一棵完全二叉树，底层是一个数组

堆的存储方式

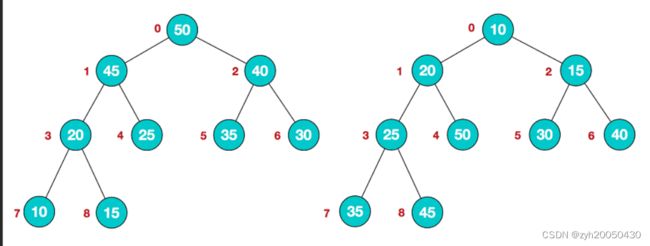
小根堆：父节点不大于俩个孩子节点；大根堆：父节点不小于俩个孩子节点。如下：

堆的创建

堆的创建以及堆的向下调整

以创建小根堆为例，要注意被调整的根节点对应的左右子树必须已满足堆的性质（即已经是小根堆）这就要求我们从最后一棵子树开始调整，逐渐往上走（注意，这不是向上调整。我们说的向下调整是争对于每颗子树来说的）

向下调整就是：在左右孩子中找到最大值，如果这个值比根节点大，就让这个值和根节点进行交换，交换完后向下走（就是原来的进行了交换的孩子节点变成父节点，再找对应的左右孩子）再重复上述操作。

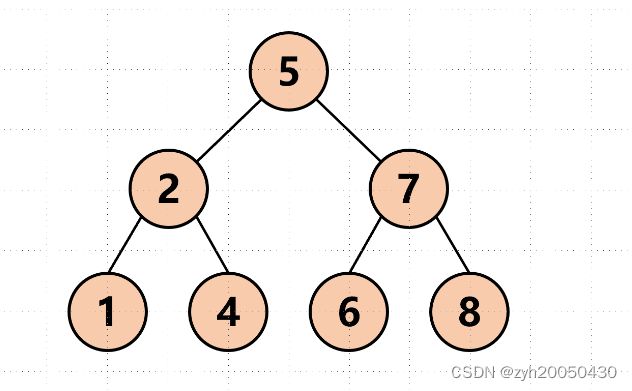
例如下图：

由于被调整的根节点的子树必须已经是小根堆，所以我们要从最后一刻子树开始调整。已知一共七个节点，最后一共节点的下标为6，所以最后一棵子树的根节点下标为(6-1)/2，即7的下标为2。先调整768，6和8中最小为6，6比7小，交换，然后向下调整向下走，根节点变为6，6的下标为5，所以左孩子节点下表为2*5+1=11，但11大于6，所以超出了范围，不用再向下了，所以结束这一组，再进行下一组，下一组是214；最后一组是以5为根节点的这组，5的左右子树由于上面的调整，已经满足小根堆的性质，所以可以对5进行向下调整。

最后调整完的层序遍历的结果为1562478.

代码如下：

private void swap(int i,int j){
        int tmp=i;
        i=j;
        j=tmp;
    }
    public void siftdown(int parent,int end){
        int child=parent*2+1;//左孩子下标
        while(child elem[child + 1]) {
                child = child + 1;//保证child指向最小的
            }
            if (elem[child] < elem[parent]) {
                swap(elem[child], elem[parent]);
            }
            //再向下调整
            parent = child;
            child = parent * 2 + 1;
        }
    }

我们在传参时，end就是elem中的元素个数（对于上面那个二叉树来说就是7）我们要保证孩子节点的下标要小于节点个数，这样孩子节点才存在。

但这段代码有问题：我们是保证了child小于end，但最后一颗子树不一定有右孩子，所以还要保证child+1小于end；其次，如果elem[child] > elem[parent]那说明已经完全调整完毕，就不用再向下判断，直接break即可；最后，交换代码有问题，因为i，j只是临时拷贝，这样是交换不了的。所以上面代码修改后变为：

    private void swap(int i,int j){
        int tmp=elem[i];
        elem[i]=elem[j];
        elem[j]=tmp;
    }
    public void siftdown(int parent,int end){
        int child=parent*2+1;//左孩子下标
        while(child elem[child + 1]) {
                child = child + 1;//保证child指向最小的
            }
            if (elem[child] < elem[parent]) {
                swap(child,parent);
                //再向下调整
                parent = child;
                child = parent * 2 + 1;
            }
            else{
                //已经满足堆的性质，不用再调整。
                break;
            }
        }
    }

时间复杂度分析

设共有n个元素，则一次向下调整的时间复杂度为log2n（每交换一次就往下走一层）

那么创建一个堆的时间复杂度呢？

创建堆要从最后一个子树开始调整，即第h-1层，该层有2^(h-2)个元素，只需要向下调整一层，然后是第h-2层，该层有2^(h-3)个元素，需要向下调整两层……

所以Tn=2^0*(h-1)+2^1*(h-2)+2^2*(h-3)+……+2^(h-3)*2+2^(h-2)*1;

2*Tn=2^1*(h-1)+2^2*(h-2)+2^3*(h-3)+……+2^(h-2)*2+2^(h-1)*1;

上下相减再用等比数列求和得到了Tn=2^h-1-h;又因为2^h-1<=n,所以近似于Tn=n-log2(n+1),所以时间复杂度近似于n。

堆的创建代码为：

    public void creatHeap(){
        int parent;
        for(parent=(usedsize-1-1)/2;parent>=0;parent--){
            siftdown(parent,usedsize);
        }
    }

堆的插入以及向上调整

还是以小根堆为例

在堆中插入一个元素要用到向上调整，先将插入的元素放到堆的最后，再让这个节点与它的父节点比较，如果小于父节点，就交换，然后让子节点指向这个父节点，父节点向上移动，直到子节点大于父节点，代码如下：

    private void siftup(int child){
        int parent=(child-1)/2;
        while(parent>=0){
            if(elem[child]

这是向上调整，其时间复杂度为log2n;

那么堆的插入就可以写为：

    public void offer(int val){
        if(usedsize==elem.length){
            elem= Arrays.copyOf(elem.,elem.length*2);
        }
        elem[usedsize]=val;
        usedsize++;
        siftup(usedsize-1);
    }

根据上面的推导，可以类似推导出插入操作的时间复杂度为：log2n

假设堆的创建也采用向上调整，那么从最后一个元素开始，然后是倒数第二个元素，然后是倒数第三个元素……这样算下来只有第一个元素不用调整，所以这样会使得时间复杂度变高，此时Tn=(n+1)*(log2(n+1)-2)+2时间复杂度是：O(n*log2n);

堆的删除

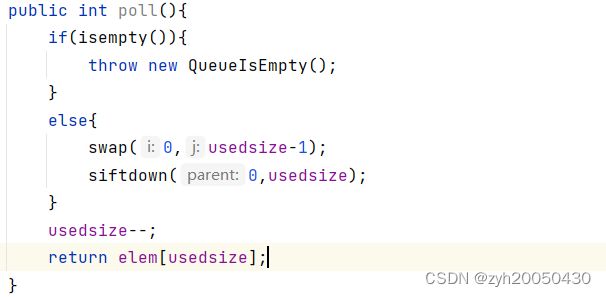
堆的删除是先让首元素和尾元素进行交换，然后再以首元素为根进行向下调整，然后usedsize-1.

代码如下:

时间复杂度为：O(log2n)。

三.PriorityQueue

这是一个泛型类，使用时必须实例化对象并传入类型

1.PriorityQueue中放置的元素必须是可以比较大小的

因为要排序，所以应该插入可以比较大小的元素

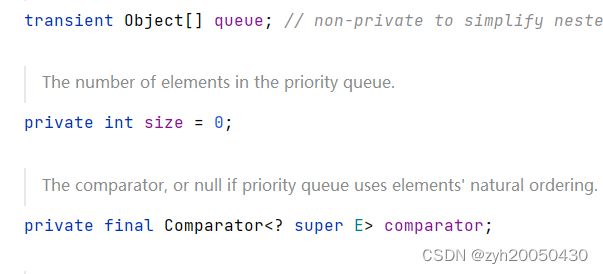
这是源码中的几个成员变量，其中第三个就是一个比较器，再看一下构造方法：

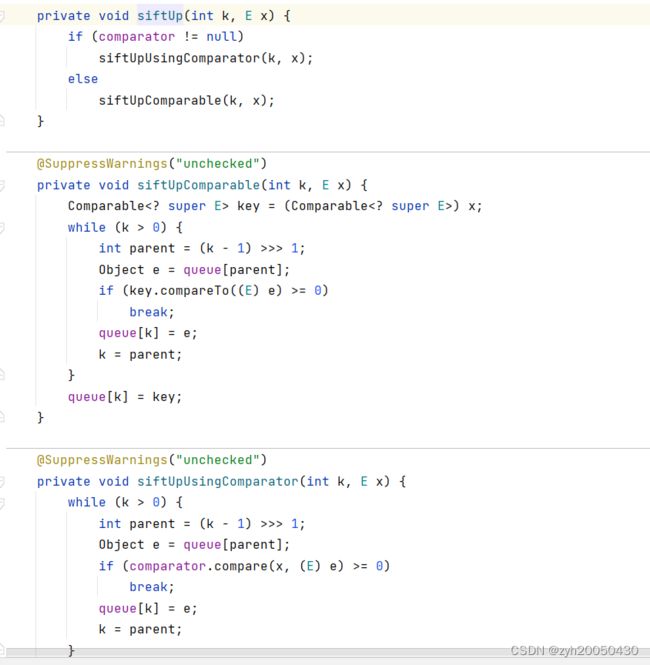
先看这几个，如果没有传入比较器，那么比较器默认为null，然后在后面的比较中就会用到Comparable接口以及compareto方法，如果传入比较器，就用传入的比较器进行比较。如下：

看向上调整的代码，comparator！=null时，用comparator，反之用comparable

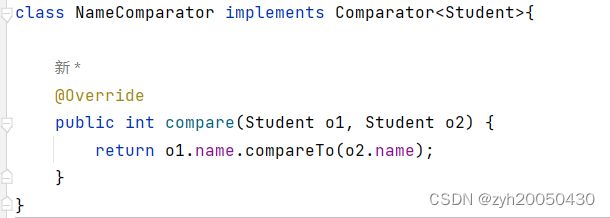
所以如果想要插入student对象，要进行如下操作：那就是在给PriorityQueue传参时传入一个自定义的比较器，如何自定义比较器呢？只要让其实现comparator接口即可，注意这是个泛型接口，一定要传入类型，如下：

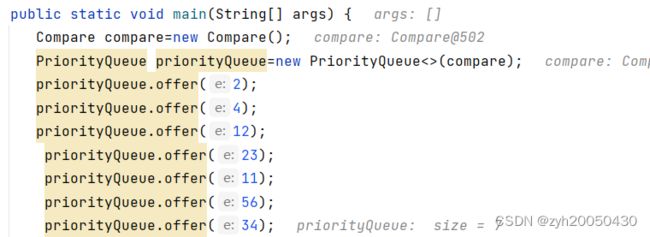
在main方法中，应该这样写：

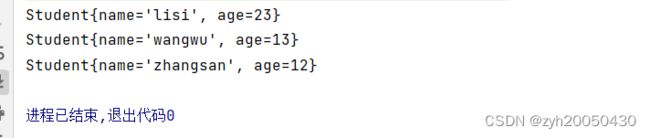
下面我们通过poll来证明这是小根堆：

2.不可以插入null对象

3.PriorityQueue默认是小根堆的存储形式

如何变成大根堆存储？先看一下源码：

我们如果能把key.compareTo((E) e）变成(E) e.compareTo(key）就好了，如下操作

通过调试就可以发现这是一个大根堆：

四.堆排序问题

如何将一个堆进行排序，使得其层序遍历的结果为从小到大或从大到小？

如果要从小到大排，就要建立大根堆，从最后一个元素开始依次向前，都与第一个元素进行交换，每换一次就要向下调整一次。调整的范围是从0到那个被交换的元素之前。

所以要定义一个end，end与大根堆堆顶元素交换，然后向下调整（结束位置就是end），end向前移动一位，再交换，再调整。每交换一次都可以讲堆顶元素放到从小到大排序时该有的位置，代码如下：

测试一下：

我这个是创建了一个小根堆，进行了从大到小排序