力扣：34.在排序数组中查找元素的第一个位置和最后一个位置

该题目比较复杂，若还没有了解过二分法的，理解这道题较难。可以参考以下两篇解题方法：

力扣：704.二分查找(c++)

力扣：35.搜索插入位置

题目：

给定一个按照升序排列的整数数组 nums，和一个目标值 target。找出给定目标值在数组中的开始位置和结束位置。

如果数组中不存在目标值 target，返回 [-1, -1]。

示例 1：

输入：nums = [5,7,7,8,8,10], target = 8
输出：[3,4]

示例 2：

输入：nums = [5,7,7,8,8,10], target = 6
输出：[-1,-1]

分析：

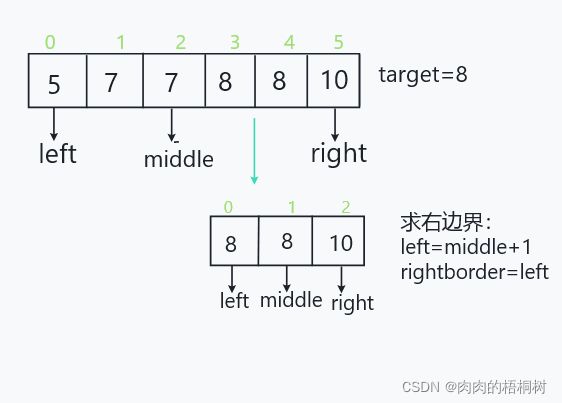
把这道题分成两部分：1、先求右边界。2、再求左边界。

• 求右边界：用二分法进行求解。若在中间的数小于给定目标值，则将范围缩小为左半边，left=middle+1；若在中间的数大于给定目标值，则将范围缩小为右半边，right=middle-1.

 

private:
    int getRightBorder(vector& nums,int target){
        int left=0;
        int right=nums.size()-1;//数组下标从0开始，所以右边界的小标为数组长度-1.
        int rightborder=-2;//记录一下rightborder没有被赋值的情况.
        while(left<=right){//当left=right，可以成立。因为此时定义目标值的范围为[left,right].
            int middle=left+((right-left)/2);//防止溢出，等同于(right-left)/2.
            if(nums[middle]>target){
                right=middle-1;//target在左区间，所以范围需缩小到[left,middle-1].
            }
            else{
                left=middle+1;//target在右区间，所以范围需缩小到[middle+1,right].
                rightborder=left;//当nums[middle]==target的时候，更新left,得到rightborder.
            }
        }
        return rightborder;
        }

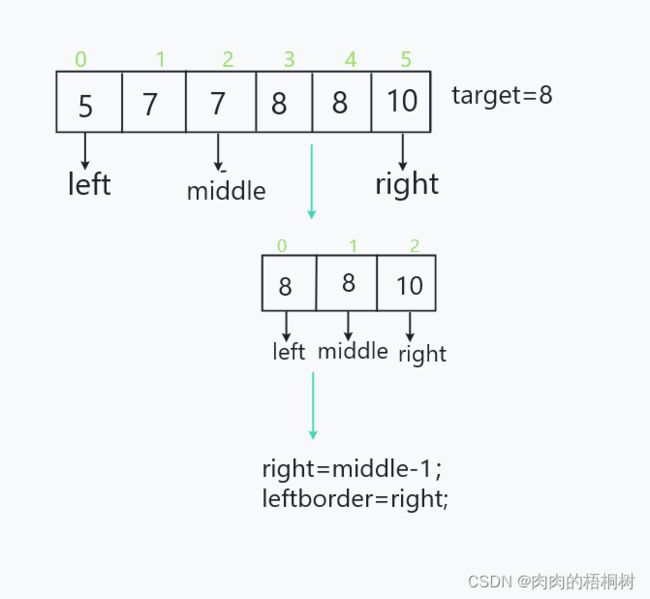
• 求左边界：同理于右边界。

private:
int getLeftBorder(vector& nums,int target){
            int left=0;
            int right=nums.size()-1;//数组下标从0开始，所以右边界的小标为数组长度-1.
            int leftborder=-2;//记录一下leftborder没有被赋值的情况.
            while(left<=right){
                int middle=left+((right-left)/2);//防止溢出，等同于(right-left)/2.
                if(nums[middle]>=target){
                    right=middle-1;//target在左区间，所以范围需缩小到[left,middle-1].
                    leftborder=right;//当nums[middle]==target的时候，更新right,得到leftborder.
                }else{
                    left=middle+1;//target在右区间，所以范围需缩小到[middle+1,right].
                }
            }
            return leftborder;
        }
};

 最后，将他们综合在一起：

class Solution {
public:
    vector searchRange(vector& nums, int target) {
        int rightborder=getRightBorder(nums,target);//对函数进行引用。
        int leftborder=getLeftBorder(nums,target);
        if(rightborder==-2||leftborder==-2){//target在数组范围的左边或右边，则表示没有被赋值。则输出{-1,-1}.
            return {-1,-1};
        }
        if(rightborder-leftborder>1){//若rightborder-leftborder>1,则说明已被赋值，则输出{leftborder+1,rightborder+1}.
            return {leftborder+1,rightborder-1};
        }
        return {-1,-1};//target在数组的范围中，但没有该数字。


    }
private:
    int getRightBorder(vector& nums,int target){
        int left=0;
        int right=nums.size()-1;//数组下标从0开始，所以右边界的小标为数组长度-1.
        int rightborder=-2;//记录一下rightborder没有被赋值的情况.
        while(left<=right){//当left=right，可以成立。因为此时定义目标值的范围为[left,right].
            int middle=left+((right-left)/2);//防止溢出，等同于(right-left)/2.
            if(nums[middle]>target){
                right=middle-1;//target在左区间，所以范围需缩小到[left,middle-1].
            }
            else{
                left=middle+1;//target在右区间，所以范围需缩小到[middle+1,right].
                rightborder=left;//当nums[middle]==target的时候，更新left,得到rightborder.
            }
        }
        return rightborder;
        }

        int getLeftBorder(vector& nums,int target){
            int left=0;
            int right=nums.size()-1;//数组下标从0开始，所以右边界的小标为数组长度-1.
            int leftborder=-2;//记录一下leftborder没有被赋值的情况.
            while(left<=right){
                int middle=left+((right-left)/2);//防止溢出，等同于(right-left)/2.
                if(nums[middle]>=target){
                    right=middle-1;//target在左区间，所以范围需缩小到[left,middle-1].
                    leftborder=right;//当nums[middle]==target的时候，更新right,得到leftborder.
                }else{
                    left=middle+1;//target在右区间，所以范围需缩小到[middle+1,right].
                }
            }
            return leftborder;
        }
};