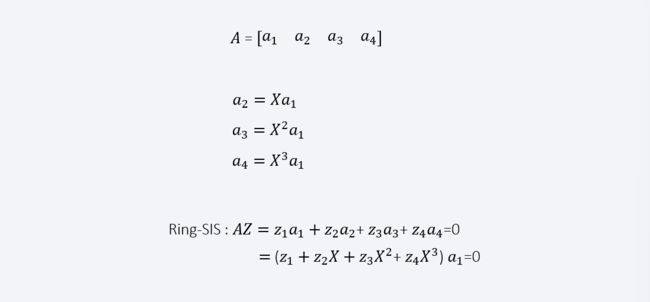SIS与LWE问题

最近一个月在学习格密码，主要参考文献是A Decade of Lattice Cryptography，也就是格十年，加上网上查的一些资料和文献。借助这篇博客，把自己对格中两大重要问题，也就是SIS与LWE问题的认识，写出来，有助于以后的复习。

首先格中有三大困难问题，也就是最糟糕的困难问题，一个是SVP问题，也就是最短向量问题；还有CVP问题，也就是最近向量问题，最后一个是SIVP，叫最短独立向量问题。而CVP里面又可以细分一下，分别是ADD与BDD难题。有限于作图能力实在太差，以后会写一篇博客把这几个问题补上。

SIS问题主要基于困难问题中的SIVP难题，而LWE则是基于BDD难题，后面会详细描述。

话不多说，直接开始。

1. SIS问题
2. LWE问题
3. 二者存在的问题
4. Ring-SIS与Ring-LWE问题
5. 总结

SIS问题

先来介绍下SIS(Small Integer Solution Problem)问题，有些抽象，需要有一定的数学基础和空间想象能力。
 

从n维整数空间中随机选取出m个向量，记为a₁,a₂,……a_m，然后找出一组非平凡解z₁,z₂,……z_m，使得z₁a₁+z₂a₂+……z_ma_m=0，注意符号$Z_q^n$,代表的是在n维空间中选取出的数据，而右下方的符号q代表的是取模，也就是把向量中的整数，全部模掉q。这是为了减少计算机的运算量，同时还能防止数据溢出。

可以思考一下，假如说，不对 z_i 进行限制会发生什么，取所有的z=0，就是一个解，那么SIS问题也就不会是一个困难问题了。同样的，大学里面学过线性代数，只需要对矩阵进行一些线性变换就可以得到AZ=0的所有解，那这个问题也很好解决。

SIS问题之所以难，难就难在所有的z_i只能取{0,1,-1}。那么求解这个问题就会变的非常困难。

那它和格有什么关系呢？
 

当不对z_i进行限制的时候，可以得出来很多解，而这些解事实上就是遍布在空间中的格点。假设S代表所有解的集合，那么我需要在S中寻找到一个短向量，当然这个向量可以不唯一。

先来看下定义格的两种形式：
 

有两种方式来定义格，第一种我们把矩阵B的每一列当作是格的基向量，而x代表对基向量的线性组合，就可以得到一个格z。是不是很抽象？
没关系，我们从二维来考虑，如果B的每一个列向量为[1,0]^T,[0,1]^T，那么x就是对这个坐标的线性组合，可以为[3,2]^T,那么所得出的格点z=[3,2]^T这个格点就是在坐标系里的坐标了。它遍布于整个坐标系。

图中的格为一个n维格。

通常为了便于计算，会取一个模q，而这个q会把坐标系里的点分为很多个区域。我们通常只需要考虑距离原点最近的那块区域就好了。

由二维到三维，再到n维也是一样。

再看第二种定义方式，这里的A矩阵里的每一列，可以类比于刚才所讲的SIS问题的a_i，而这里的Z就是z_i的线性组合。当然它的所有解就是空间中的每一个格点。如上述所说的z=[3,2]^T，它就是线性组合了格基之后的格点。现在就是要找到一个在格中的一个足够短的非零向量。

而求这个足够短的非零向量事实上是基于SIVP困难问题的，来看下什么是SIVP问题：
 

SIVP问题就是给定一个格，我们需要找到n个线性独立的向量Bx1,Bx2,Bx3,……Bxn,而且这些向量的长度都要小于等于最长的最短向量λn。再来详细介绍一下λn的由来，如图所示：
 

在二维空间中，假设存在一个格如上图，绿色的点为格的格点分布，下面给出连续极小的概念，任意选择两个向量，求它们之间的距离，而这个距离的最小值，就是第一连续极小，当然，可以通过两个向量相减的方式，来计算减去之后的向量距离原点的距离。距离从小到大，λ1就是第一连续极小，λ2就是第二连续极小，……λn就是第n连续极小。注意，这里的λn就是SIVP里的λn。

那么回顾整个过程，SIVP是如何归约到SIS问题上的，其实很简单，SIS问题就是在找一个格中的短向量z这个向量只能从[-1,0,1]里面取值，且不唯一，那么这个z事实上就是SIVP所求的n个连续极小λn。也就是说，如果我可以解决SIS问题，那么我就可以解决SIVP问题。

是不是很烧脑，如果上面的内容可以理解，接下来就可以看看SIS的应用了。

它最简单的一个应用，就是抗碰撞的hash函数。
 

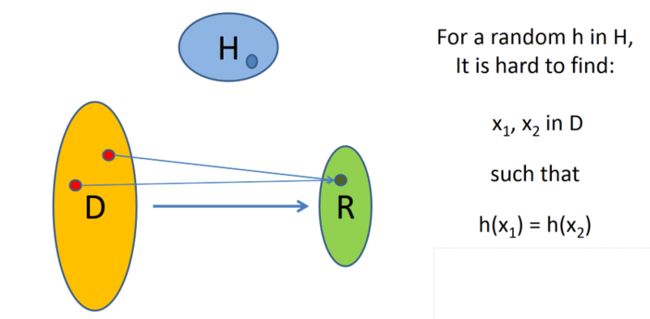
先来看看碰撞hash函数的概念，如果把D理解为定义域，R理解为值域，碰撞的意思就是我可以从D里面找到两个值x1,x2，使得函数h(x1)=h(x2)，这样就产生了碰撞，那么基于SIS的抗碰撞的哈希函数是怎么构造的呢？

 

其实很简单，假设已经存在一个随机矩阵的A，它是n*m的，可以想象成上面SIS里面的a₁,a₂,……a_m，
注意，这里的A矩阵事实上就是私钥K了，也是函数h(x)，而z₁,z₂,……z_m，就是输入向量z，这里的z只能取{0，1}，也就是我们想要hash的数据，没错，它就是只能取{0,1}，毕竟计算机里面的二进制数据也只有{0,1}两个值。我们假设存在另一组数据y₁,y₂,……y_m,使得z₁a₁+z₂a₂+……z_ma_m=y₁a₁+y₂a₂+……y_ma_m。用向量表示就是AZ=AY，把等式移动到一侧，那么A(Z-Y)=0，注意，这里的(Z-Y)的值，是可以取为{-1，0，1}的。

看到这个形式，有没有觉得很熟悉，没错，它就是SIS问题，前面我们已经论证了求解这个问题是非常困难的。那吗也就是说很难找到两组向量使得A(Z-Y)=0，也就是说在这个hash函数中，很难找到两个不同的x1,x2，使得h(x1)=h(x2)。那么也就不会产生碰撞。

注意：这里的矩阵A很有意思，因为我可以通过改变随机矩阵向量的个数m和维数n，来适应我想要hash数据的位数，以及我想要hash之后的数据长度。真的很有趣。

 
 

LWE问题

如果说SIS问题偏基础，偏理论方面的话，LWE可是实打实的偏应用了。因为基于这个问题，可以构造公钥密码学，不经意传输，全同态加密等等。

那么LWE是什么呢？

 

可以叫它错误学习，Serach版本的LWE，就是给定m组数据，每组数据里面包含两个值，一个是矩阵A，A的构造就是[a₁,a₂,……a_m]，另一个就是b^t，其中b^t=s^tA+e^t。
这里的A和前面所说的SIS问题里的矩阵A类似。

这里的e^t代表的是一个噪声值，它很小，但是不可忽略，而且它是满足高斯分布的。

Serach版本的LWE就是要从这些数据中找到密码向量s。
Decision版本的LWE就是要从这些数据中找到一组(A,b)，其中它是不满足基于s的结果的数据。也就是说它跟别的数据不同。

来分析一下Search版本的LWE问题的苦难度，把上面的b^t换一种形式来表达，用b_i=a_ix+e_i，来表示，那么可以形成如下图所示的关系：
 

如果没有噪声值e的话,那么这个方程组非常好解，利用大学里面学到的线性代数，解非齐次线性方程就好了。但是加上了噪声值之后，就不好找了。因为噪声值是满足高斯分布的，它并不是一个单一的数据。

顺便说一下，解决LWE问题有两种方式，第一种是找到秘密向量x,另一种是找到噪声值e满足的高斯分布。这就涉及到更加偏向于数学的知识了，还要利用到抽象代数。

加入说解出来了一个秘密向量s，我如何判断这个向量是否是正确的解呢？
直接让b-As即可。如果得到的值很小很小，那就是噪声值，说明s是正确的，否则结果将会遍布整个空间。

讲到这里只需要知道，这个问题非常的难，可是它是怎么跟格扯上关系的呢？接下来就说说格中的另一大困难问题，CVP问题。

 

先来看一下理论介绍，CVP(Closest Vector Problem)问题就是最近向量问题。给定一个格，然后在这个格中再给定一个点t，这个点不在格点上，但是会在格点的周围，CVP问题就是计算出距离点t最近的一个格点，它到这个点t的距离d>=覆盖半径u(L)。然后根据这个距离的大小，CVP又有两个版本。

BDD版本最短距离d<λ₁/2，在这种情况下，只能有一个解，这个解一定是距离点t最近的向量。
ADD版本规定最短距离d>=u(L),这里的u(L)代表的是覆盖半径。这种情况下，解不唯一。

类比一下LWE问题，如果我们把Ax当作是一个格点的话，那么噪声值就像是一个移动距离，加上噪声值以后，就相当于BDD困难问题里的点t，我们要寻找一个距离这个点t最近的一个格。因为BDD是一个格上最糟糕的困难问题，所以基于BDD的LWE问题也非常难。

那么这个问题就可以很好的应用到格上了。

接下来看看LWE的应用吧。PKE（公钥加密）

公钥加密方案中，(A,b)作为公钥，s就是私钥。

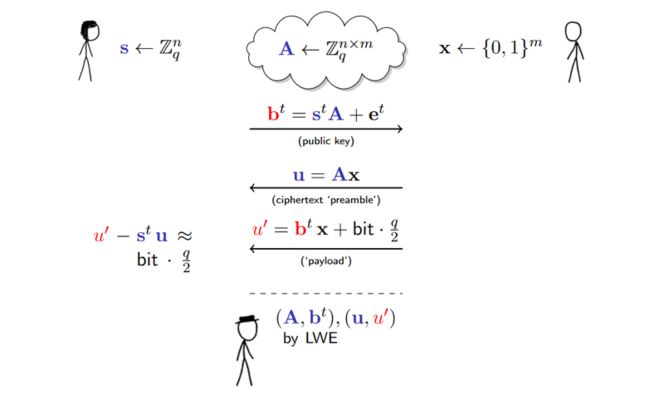
如果现在有两方Alice和Bob想要进行通信，左边为Alice,右边为Bob，Bob想要给Alice发送1bit的信息。

首先，Alice会把公钥公布出去，把b^t=s^tA+e^t发送给Bob作为公钥。
Bob会生成一个向量m维的向量x。然后Bob把u=Ax作为密文序列，发送给Alice，然后计算u^’=b^tx+bit*q/2。也发送给Alice。

那么Alice如何验证并解密Bob发送的密文信息呢？

利用私钥s。直接让u^’-s^tu=e^tx+bit*q/2。

由于噪声值e^t非常小，所以e^tx可以忽略不记。加入Bob想要发送的bit为0，那么结果就近似为0，如果想要发送的消息为1，那么结果就近似为q/2。
这是密钥值s为正确的情况下，如果不正确，那么结果很显然是要遍布整个空间的。

有没有很神奇？

二者存在的问题

我们先来对SIS与LWE进行一下比较：
 

1.从形式上来看，二者形式很类似，SIS所要解决的是Az=0,找一个短向量’z’不等于0。LWE所要解决的问题是给定许多组(A,b^t=s^tA+e^t)，找出一个例外（这是判定类型的LWE）。

2.从解的数量上来看，SIS可以有许多解，LWE只能有一个解。

3.LWE问题可以规约到SIS，也就是说如果我解决了SIS问题，找到了一组短向量z，使得Az=0，那么LWE里面的b^tz=e^tz。这是判定类型的LWE，如果结果很小，就说明这一组数据是正确的。如果结果遍布整个空间，就说明这一组数据就是那个例外。也就解决了Decision-LWE。那么SIS问题可以归约到LWE吗？目前我所了解的文献里面暂时还找不到。

4.再来看看二者的应用，SIS的应用主要是单向函数/抗碰撞的hash。身份认证，数字签名等。而LWE的应用主要在公钥加密，基于身份的加密，全同态加密等等。

5.Russell Impagliazzo在1995年提出了P与NP问题的五个层级，SIS问题就位于mincrypt层级，也就是存在单向的加密函数，但是没有公钥加密。而LWE问题则位于Cryptomania层级，两方可以通过公钥加密，然后通过私钥解密。

存在的问题

这两种难题都存在一个共同的问题，那就是占用的存储空间比较大，A矩阵存放着不同的数据，内存需要开辟大块的空间来存这些数据，最重要的是，在计算的时候，乘法运算本身就是计算机最讨厌的计算，然后在进行运算时，SIS与LWE几乎全是乘法运算。得到的值也许会很大，所以计算机在内存中开辟出来的存储空间非常大。

然后就是时间复杂度问题，一般情况下A矩阵为n*m列，而对于m的要求为m>=nlogn，那么在运算的时候，时间复杂度就是O（n²）。

综合以上信息，如果可以对A矩阵进行一些优化的话，就可以把时间和空间复杂度降下来，从而减少运算量，那么该怎么办呢？

ring-lwe与ring-sis就来了！！！
 
 

ring-lwe与ring-sis

先来看一个矩阵：

 
 
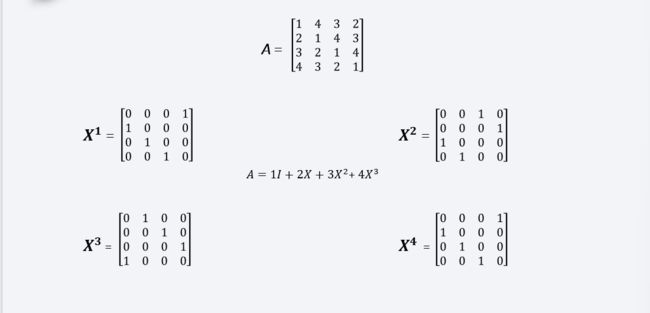
先看矩阵R，有没有发现一些规律，它的第一列经过向下循环一位以后形成了第二列，第二列经过循环过后形成了第三列，第三列再循环一列就形成了第四列。这么有规律的事情，它可不可以用一个矩阵来有效的表示呢？

数学上来说，我可以定义一个循环矩阵，把A的第一列向量记为a₁，那么第二列就是Xa₁，第三列就是X²a₁，第四列就是X³a₁。如下图所示：

如果需要更多的列，只需要不断循环就好了。

如果把这里的矩阵A叫做一个环的话，它通常被认为是一个n次多项式，形式是A=Z[X]/(f(x))，上图中的f(x)取的是xⁿ-1。

这个商环有什么意义呢？如图：

 

可以看到，当i=n-1时，x * xⁱ=xⁱ⁺¹，这个环并不会有任何数据上的变化，但是，当i=n-1时，x * xⁱ=xⁿ，由于xⁿ，要比环大1，所以最终的值就是1。当旋转的次数变多的时候，也就是超过了n-1阶的时候，位于下面的数字，就又回到了上面继续循环。

整个过程，只用到了第一组向量，如果我把它设为a₁，那么整个A矩阵，我就可以通过a₁循环产生。

这样整个A矩阵就可以通过多项式环来表示出来了。

接下来继续看看，在SIS中它是如何应用的，SIS是这样定义的，z₁a₁+z₂a₂+z₃a₃₊z₄a₄=0。解释一下，这里的a₁,a₂……a₄为一个向量，z₁,z₂,……z₄为一个数字,且属于{0，1，-1}。
对上式做进一步的整理：(z₁+z₂X+z₃X²+z₄X³)a₁=0。这里如果把(z₁+z₂X+z₃X²+z₄X³)看成是一个环Z的话，此时的乘法就变成了多项式a₀Z之间相乘。
由于A是一个多项式环。里面的每一个向量都可以用a₁表示，那么在进行上述计算的时候，复杂度直接降到了O(n)。而且存储的时候，我也只需要存储第一组向量即可，对于时间复杂度和空间复杂度，都大大的降低了。

综上所述，采用环的方法，只需要存储一个向量a₁，剩下的通过循环移位就可以。当然，这也存在结构化风险。

因为xⁿ-1是可以被约分的。所以目前主流的多项式环采用的形式为f(x)=xⁿ+1。

环lwe与环sis，二者虽然计算更简单了，但是它的安全性相比于lwe,sis二者之间并没有提高，相反正因为它有结构化的特点，所以较于后者更加易于攻破。

 
 

总结

LWE与SIS二者可以说是格密码的基础，基于这两个困难问题可以设计很多优秀的密码学方案。

2020年欧密有一篇关于OT的论文，它主要就是基于LWE的变体LPN问题设计的。

在LWE的应用中，它难就难在计算量非常大，如果我可以把值取的小一些，比如说：我把模q直接一步降到2。那么数据就只剩下0，1了。而这也就是LPN的问题的由来。

只不过此时噪声值不再满足高斯分布了，它满足的是伯努利分布。

总的来说，一定会有很多好玩的设计等着探索，它很新，也很难，只要能钻进去，一定可以获得很多收获。