数字信号处理--几种常见的数字滤波器实现原理
参考:数字信号处理公式变程序(四)—巴特沃斯滤波器(上)
滤波器
现代滤波器理论研究的主要内容是从含有噪声的数据记录中估计出信号的某些特征或者信号本身,估计出的信号的信噪比将比原信号的高,将信号和噪声都视为随机信号,利用其统计特征导出一套最佳的估计算法。
设计的步骤:
- 给出所需的滤波器的技术指标;
- 设计一个 H ( z ) H_(z) H(z)使其逼近所需的技术指标;
- 实现所设计的 H ( z ) H_(z) H(z),其中步骤2是本章和下一章所讨论的主要内容。

按功能分类

按相位响应分为线性相位和非线性相位;按特殊要求分为最小相位滞后滤波器、梳状滤波器等;按冲激响应分为无限冲激响应数字滤波器(IIR:有反馈,无限长),有限冲激响应数字滤波器(FIR:无反馈,有限长)
示例:巴特沃斯滤波器
滤波器设计
**目的:**找到一个满足技术指标要求的可实现的因果稳定的数字滤波器来逼近理想的滤波器幅度特性。
**思路:**间接法-先设计模拟滤波器,然后通过双线性变换法来制作数字低通滤波器、数字高通滤波器、数字带通滤波器、数字带阻滤波器
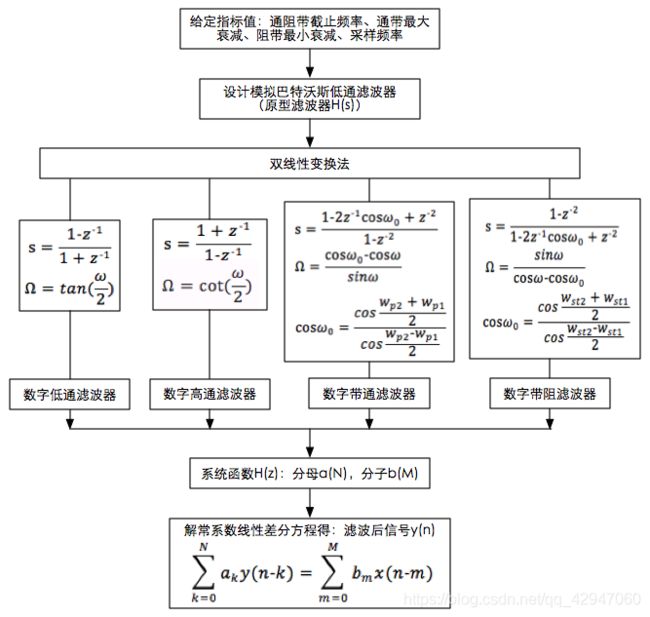
模拟滤波器设计:

通带截止频率wp,阻带截止频率ws, 通带最大衰减1-δ1(Rp(dB)), 阻带最小衰减δ2(As(dB)) 。
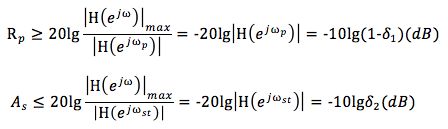
1、确定技术指标: Ω p o r s = 2 ∗ π ∗ f p o r s \Omega_{p\,or\,s}=2*\pi*f_{p\,or\,s} Ωpors=2∗π∗fpors, 1 − δ 1 1-δ1 1−δ1, δ 2 δ2 δ2, Ω c ( 3 d B 频 率 ) \Omega_{c}(3dB频率) Ωc(3dB频率) Ω c ≥ l g ( 1 0 0.1 A s − 1 1 0 0.1 A p − 1 ) = Ω c p \Omega_{c}\geq lg(\frac{10^{0.1As}-1}{10^{0.1Ap}-1})=\Omega_{cp} Ωc≥lg(100.1Ap−1100.1As−1)=Ωcp Ω c ≤ l g ( Ω s 1 0 0.1 A s − 1 ) = Ω c s \Omega_{c}\leq lg(\frac{\Omega_{s}}{10^{0.1As}-1})=\Omega_{cs} Ωc≤lg(100.1As−1Ωs)=Ωcs
2、计算滤波器所需阶数N,C N = l g ( 1 0 0.1 A s − 1 1 0 0.1 A p − 1 ) / ( 2 ∗ l g ( λ s ) ) N=lg(\frac{10^{0.1As}-1}{10^{0.1Ap}-1})/(2*lg(\lambda_{s})) N=lg(100.1Ap−1100.1As−1)/(2∗lg(λs)) C 2 = 1 0 α p / 10 − 1 C^{2}=10^{\alpha_{p}/10}-1 C2=10αp/10−1
3、查表确定归一化低通滤波器系统函数 G ( p ) G(p) G(p)
G ( p ) = 1 ( p − p 1 ) ( p − p 2 ) ( p − p 3 ) . . . ( p − p N ) G(p)=\frac{1}{(p-p_{1})(p-p_{2})(p-p_{3})...(p-p_{N})} G(p)=(p−p1)(p−p2)(p−p3)...(p−pN)1
因为几点成对共轭出现,所以可以按N的奇偶性如下表示:
N 为 偶 G ( p ) = ∏ K = 1 N / 2 G k ( p ) N为偶 G(p)=\prod_{K=1}^{N/2}G_{k}(p) N为偶G(p)=K=1∏N/2Gk(p) N 为 奇 G ( p ) = 1 p + 1 ∏ K = 1 ( N − 1 ) / 2 G k ( p ) N为奇 G(p)=\frac{1}{p+1}\prod_{K=1}^{(N-1)/2}G_{k}(p) N为奇G(p)=p+11K=1∏(N−1)/2Gk(p)
G k ( p ) = 1 p 2 − 2 p c o s ( 2 k + N − 1 2 N π ) + 1 G_{k}(p)=\frac{1}{p^{2}-2pcos(\frac{2k+N-1}{2N}\pi)+1} Gk(p)=p2−2pcos(2N2k+N−1π)+11 极 点 : p k = e x p ( j 2 k + N − 1 2 N π ) k = 1 , . . N 极点:p_{k}=exp(j\frac{2k+N-1}{2N}\pi)\,\,k=1,..N 极点:pk=exp(j2N2k+N−1π)k=1,..N
4、将Has(s)转换为所需类型的低通滤波器系统函数G(s),因为 p = s Ω c p=\frac{s}{\Omega_{c}} p=Ωcs,所以
G ( s ) = G ( s Ω c ) G(s)=G(\frac{s}{\Omega_{c}}) G(s)=G(Ωcs)
关于G§还有一种查表计算法:
G ( p ) = 1 ( p − p 1 ) ( p − p 2 ) ( p − p 3 ) . . . ( p − p N ) = 1 1 + a 1 p + a 2 p 2 + . . . + a N p N G(p)=\frac{1}{(p-p_{1})(p-p_{2})(p-p_{3})...(p-p_{N})}=\frac{1}{1+a_{1}p+a_{2}p^{2}+...+a_{N}p^{N}} G(p)=(p−p1)(p−p2)(p−p3)...(p−pN)1=1+a1p+a2p2+...+aNpN1

模拟滤波器数字化
方法有冲激响应不变法、阶跃响应不变法和双线性变换法等。
冲激响应不变法(适合低通和带通);双线性变换法:
s->z
简单说来,将水平面的转移函数映射到z平面,就是数字化,变换公式在思路流程图中。
实际应用滤波的过程就是解常系数线性差分方程的过程。y(n)为滤波后信号,x(n)为滤波前信号
y ( n ) = ∑ m = 0 M b m x ( n − m ) − ∑ k = 1 N a k y ( n − k ) y(n)=\sum^{M}_{m=0}b_{m}x(n-m)-\sum^{N}_{k=1}a_{k}y(n-k) y(n)=m=0∑Mbmx(n−m)−k=1∑Naky(n−k)
其中 a k a_{k} ak, b m b_{m} bm分别为系统函数H(z)分母与分子的系统数组
滤波器的素质转模拟技术指标的规则
低通
截止频率 f p f_{p} fp,阻带起始频率 f s f_{s} fs,通带最大衰减 α p α_{p} αp,阻带最小衰减 α s α_{s} αs,由此计算N值 λ p = 1 \lambda_{p}=1 λp=1 λ s = ( f s / f p ) \lambda_{s}=(f_{s}/f_{p}) λs=(fs/fp) p = s Ω p p=\frac{s}{\Omega_{p}} p=Ωps
高通
截止频率 f p f_{p} fp,阻带起始频率 f s f_{s} fs,通带最大衰减 α p α_{p} αp,阻带最小衰减 α s α_{s} αs,由此计算N值 λ p = 1 \lambda_{p}=1 λp=1 λ s = ( f p / f s ) \lambda_{s}=(f_{p}/f_{s}) λs=(fp/fs) p = s Ω p p=\frac{s}{\Omega_{p}} p=Ωps
带通
Ω = ω f \Omega=\omega f Ω=ωf 通带下限截止频率 ω 1 \omega_{1} ω1 通带上限截止频率 ω 3 \omega_{3} ω3 下阻带截止频率 ω z l \omega_{zl} ωzl 上阻带截止频率 ω z h \omega_{zh} ωzh 通频带宽 ω B W = ω 3 − ω 1 \omega_{BW}=\omega_{3}-\omega_{1} ωBW=ω3−ω1 定义中心频率 ω 2 2 = ω 1 ω 3 \omega_{2}^{2}=\omega_{1} \omega_{3} ω22=ω1ω3
将频率归一化处理:
η z l = ω z l / ω B W ; η z h = ω z h / ω B W ; η = ω 1 / ω B W ; η = ω 3 / ω B W \eta_{zl}=\omega_{zl}/\omega_{BW};\eta_{zh}=\omega_{zh}/\omega_{BW};\eta=\omega_{1}/\omega_{BW};\eta=\omega_{3}/\omega_{BW} ηzl=ωzl/ωBW;ηzh=ωzh/ωBW;η=ω1/ωBW;η=ω3/ωBW
因为 η 3 − η 1 = 1 = > λ p = 1 \eta_{3}-\eta_{1}=1=>\lambda_{p}=1 η3−η1=1=>λp=1
λ s = η z h 2 − η 2 2 η z h \lambda_{s}=\frac{\eta_{zh}^{2}-\eta_{2}^{2}}{\eta_{zh}} λs=ηzhηzh2−η22 − λ s = η z l 2 − η 2 2 η z l -\lambda_{s}=\frac{\eta_{zl}^{2}-\eta_{2}^{2}}{\eta_{zl}} −λs=ηzlηzl2−η22 p = s 2 + Ω 1 Ω 3 s ( Ω 3 − Ω 1 ) p=\frac{s^{2}+\Omega_{1}\Omega_{3}}{s(\Omega_{3}-\Omega_{1})} p=s(Ω3−Ω1)s2+Ω1Ω3 最终 λ s \lambda_{s} λs取上绝对值的最小值
带阻
λ s = η z h η z h 2 − η 2 2 \lambda_{s}=\frac{\eta_{zh}}{\eta_{zh}^{2}-\eta_{2}^{2}} λs=ηzh2−η22ηzh − λ s = η z l η z l 2 − η 2 2 -\lambda_{s}=\frac{\eta_{zl}}{\eta_{zl}^{2}-\eta_{2}^{2}} −λs=ηzl2−η22ηzl p = s ( Ω 3 − Ω 1 ) s 2 + Ω 1 Ω 3 p=\frac{s(\Omega_{3}-\Omega_{1})}{s^{2}+\Omega_{1}\Omega_{3}} p=s2+Ω1Ω3s(Ω3−Ω1) 最终 λ s \lambda_{s} λs取上绝对值的最小值
G ( p ) G(p) G(p)公式
巴特沃斯(Butterworth)
∣ G ( j Ω ) ∣ 2 = 1 1 + C 2 ( Ω 2 ) N |G(j\Omega)|^{2}=\frac{1}{1+C^{2}(\Omega^{2})^{N}} ∣G(jΩ)∣2=1+C2(Ω2)N1
G ( p ) = 1 ( p − p 1 ) ( p − p 2 ) . . . ( p − p N ) G(p)=\frac{1}{(p-p_{1})(p-p_{2})...(p-p_{N})} G(p)=(p−p1)(p−p2)...(p−pN)1
C = 1 0 α p / 10 − 1 C=10^{\alpha_{p}/10}-1 C=10αp/10−1
N = l g ( 1 0 0.1 A s − 1 1 0 0.1 A p − 1 ) / ( 2 ∗ l g ( λ s ) ) N=lg(\frac{10^{0.1As}-1}{10^{0.1Ap}-1})/(2*lg(\lambda_{s})) N=lg(100.1Ap−1100.1As−1)/(2∗lg(λs))
切尔雪夫I型(Chebyshev-I)
∣ G ( j Ω ) ∣ 2 = 1 1 + ε 2 C n 2 ( Ω ) |G(j\Omega)|^{2}=\frac{1}{1+\varepsilon^{2}C^{2}_{n}(\Omega)} ∣G(jΩ)∣2=1+ε2Cn2(Ω)1
G ( p ) = 1 ε × 2 n − 1 ∏ k = 1 n ( p − p k ) G(p)=\frac{1}{\varepsilon \times 2^{n-1}\prod_{k=1}^{n}(p-p_{k})} G(p)=ε×2n−1∏k=1n(p−pk)1
ε 2 = 1 0 α p / 10 − 1 \varepsilon^{2}=10^{\alpha_{p}/10}-1 ε2=10αp/10−1
a 2 = 1 0 0.1 A s − 1 1 0 0.1 A p − 1 a^{2}=\frac{10^{0.1As}-1}{10^{0.1Ap}-1} a2=100.1Ap−1100.1As−1
N = a r c o s h a a r c o s h λ s N=\frac{arcosha}{arcosh\lambda _{s}} N=arcoshλsarcosha
注: a r c o s h ( x ) = l n ( x + s q r t ( x 2 − 1 ) ) arcosh(x)=ln(x+sqrt(x^2-1)) arcosh(x)=ln(x+sqrt(x2−1))
切尔雪夫II型(Chebyshev-II)
∣ G ( j Ω ) ∣ 2 = 1 1 + ε 2 [ C n 2 ( Ω s ) C n 2 ( Ω s / Ω ) ] 2 |G(j\Omega)|^{2}=\frac{1}{1+\varepsilon^{2}[\frac{C_{n}^{2}(\Omega_{s})}{C_{n}^{2}(\Omega_{s}/\Omega)}]^{2}} ∣G(jΩ)∣2=1+ε2[Cn2(Ωs/Ω)Cn2(Ωs)]21
椭圆滤波器
∣ G ( j Ω ) ∣ 2 = 1 1 + ε 2 ⋃ n 2 ( Ω ) |G(j\Omega)|^{2}=\frac{1}{1+\varepsilon^{2}\bigcup_{n}^{2}(\Omega)} ∣G(jΩ)∣2=1+ε2⋃n2(Ω)1