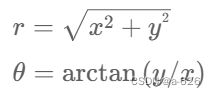假期刷题打卡--Day8
1、MT1051四边形坐标
输入四边4个顶点A,B,C,D的坐标(x,y),计算并输出四边形面积。
格式
输入格式:
依次输入4个顶点A,B,C,D的坐标(x,y),四边形一定是凸四边形,整型,空格分隔。
输出格式:
输出实型,保留2位小数。
样例 1
输入:
0 0 1 0 5 5 0 1
输出:
5.00
备注
分解成2个三角形,三角形面积公式: S=1/2 * |x1y2-x1y3+x2y3-x2y1+x3y1-x3y2|
实现代码
#include
using namespace std;
int main( )
{
int x1,y1,x2,y2,x3,y3,x4,y4;
scanf("%d %d %d %d %d %d %d %d",&x1,&y1,&x2,&y2,&x3,&y3,&x4,&y4);
double s1,s2,s;
s1 = 1.0/2.0 * abs(x1*y2-x1*y3+x2*y3-x2*y1+x3*y1-x3*y2);
s2 = 1.0/2.0 * abs(x1*y4-x1*y3+x4*y3-x4*y1+x3*y1-x3*y4);
s = s1 + s2;
printf("%.2f",s);
return 0;
} 我原本理解的就是将四边形分成两个三角形,然后使用给出的计算公式解决,结果发现,只能通过一个用例,这是为什么呢?
解决过程
参考了一下评论区的大佬的说法,是因为A,B,C,D 四个点的位置不确定(这四个的位置是随机的,所以需要考虑到全部的可能性),所以求四个三角形面积再除以2。而我前面的思路是,直接确定ABCD就在某个位置,然后直接分成两个三角形去计算,所以就只能通过一个用例。
注意:在思考不确定问题的时候,要考虑到所有情况,否则会错哦。
最终实现代码:
#include
using namespace std;
int main( )
{
int x1,y1,x2,y2,x3,y3,x4,y4;
scanf("%d %d %d %d %d %d %d %d",&x1,&y1,&x2,&y2,&x3,&y3,&x4,&y4);
double s1,s2,s3,s4,s;
//A,B,C,D 四个点的位置不固定,所以求四个三角形面积再除以2
s1 = 1.0/2.0 * abs(x1*y2-x1*y3+x2*y3-x2*y1+x3*y1-x3*y2);
s2 = 1.0/2.0 * abs(x1*y4-x1*y3+x4*y3-x4*y1+x3*y1-x3*y4);
s3 = 1.0/2.0 * abs(x2*y4-x2*y3+x4*y3-x4*y2+x3*y2-x3*y4);
s4 = 1.0/2.0 * abs(x1*y2-x1*y4+x2*y4-x2*y1+x4*y1-x4*y2);
s = (s1 + s2 + s3 + s4)/2;
printf("%.2f",s);
return 0;
}
2、MT1052直角坐标到极坐标的转换
请编写一个简单程序,实现直角坐标(x,y)到极坐标 (r,θ)的转换。数学中,极坐标系是一个二维坐标系,其中平面上的每个点由一个夹角和一段相对中心点——极点(相当于我们较为熟知的直角坐标系中的原点)的距离来表示。PI=3.1415926
其中:
格式
输入格式:
输入float型,空格分隔
输出格式:
输出float型,空格分隔,保留1位小数
样例 1
输入:
1 1
输出:
1.4 45.0
本题难点
角度制,就是用角的大小来度量角的大小的方法。
弧度制,就是用弧的长度来度量角的大小的方法。
- 了解arctan在c语言中的表示方式:atan()函数;
- 角的弧度制转为角度值的方法:角度数=180°×弧度值÷π
atan() 函数是 cmath 头文件的库函数,用于求给定数的反正切(arctan)的主值,它接受一个数 (
x) 并返回反正切的主值x以弧度表示。
弧度制转角度制:角度数=180°×弧度值÷π
实现代码
#include
#define PI 3.1415926
using namespace std;
int main( )
{
float x,y,r,z;
scanf("%f %f",&x,&y);
r = sqrt(pow(x,2)+pow(y,2));
// z = arctan(y/x); 这里我就犯了错,因为不知道编程中的表示,就直接将公式套上去了
z = atan(y/x) * 180 / PI;//这就是将弧度转为角度的办法
printf("%.1f %.1f",r,z);
return 0;
} atan(y/x) * 180 / PI的解释:
- atan(y/x) 表示计算 y 和 x 的商的反正切值。它是一个三角函数,返回的结果是一个角度,表示 y/x 所对应的角的大小。
- 这个语句的功能是计算给定 y 和 x 值所对应的角的角度值。它将 y 和 x 视为直角三角形的两条边,通过反正切函数(arctan)计算出对应角的弧度值,然后将其转换为角度制。
注意:在本题中,变量不能直接用θ,至于为什么,这就和变量命名规则有关了。
变量命名规则:
1) 变量名是字母、数字、下划线的组合,开头必须是字母或下划线,不能是数字。实际编程中最常用的是以字母开头,而以下划线开头的变量名是系统专用的。
2) 变量名中的字母是区分大小写的。比如 a 和 A 是不同的变量名,num 和 Num 也是不同的变量名。
3) 变量名绝对不可以是C语言关键字(若不知道,可自行查阅,也可看下一块),这一点一定要记住!
4) 变量名中不能有空格。
C语言关键字:共32个
1、数据类型关键字
基本数据类型(5个):void、char、int、float、double
类型修饰关键字(4个):short、long、signed、unsigned
复杂类型关键字(5个):struct、union、enum、typedef、sizeof(得到特定类型或特定类型变量的大小)
存储级别关键字(6个):auto、static、register、extern、const、volatile
2、流程控制关键字
跳转结构(4个):return、continue、break、goto
- continue:结束当前循环,开始下一轮循环
- break:跳出当前循环或switch结构
- goto:无条件跳转语句
分支结构(5个):if、else、switch、case、default
循环结构(3个):for、 do、while
具体功能,可自行查阅。
3、MT1053极坐标到直角坐标的转换
请编写一个简单程序,实现极坐标 (r,θ)到直角坐标(x,y)的转换。数学中,极坐标系是一个二维坐标系,其中平面上的每个点由一个夹角和一段相对中心点——极点(相当于我们较为熟知的直角坐标系中的原点)的距离来表示。PI=3.1415926
其中:
x = r × cos( θ )
y = r × sin( θ )
格式
输入格式:
输入实型,空格分隔
输出格式:
输出实型,逗号分隔,保留2位小数
样例 1
输入:
1.4142 45
输出:
1.00,1.00
本题难点
角度制转弧度制:弧度值=角度数÷180°×π
实现代码
#include
#define PI 3.1415926
using namespace std;
int main( )
{
double x,y,r,z;
scanf("%lf %lf",&r,&z);
x = r * cos(z/180.0*PI);
y = r * sin(z/180.0*PI);
printf("%.2f,%.2f",x,y);
return 0;
}
在今天的题目中,第一道题的易忽略点就是ABCD的位置的不确定性;第二三道题的重点就在于角度制化弧度制和弧度制画角度制的问题。
直角坐标到极坐标:弧度画角度 角度数=弧度值*180°/PI
极坐标到直角坐标:角度化弧度 弧度值=角度数/180°*PI
我记忆的方法
理解当前坐标,乘以变换后坐标相关格式,另一个除掉就(可以表述为:当前坐标定方法,化后坐标定乘谁)。
解释:
直角坐标转极坐标:直角坐标一般是实型的数,没有角度,所以转换的时候就是将弧度值转换为角度值,180°当然表示角度,所以乘以180°。
极坐标转直角坐标:极坐标一般是一个半径,一个角,所以转换的时候就是将角度转为弧度值,而弧度值一般为实型,PI约为3.1415926,与实型格式上相似,就乘以PI。
明天继续吧。