JavaSE笔记06 二维数组+数组练习题详解

JavaSE笔记06 二维数组+数组练习题详解

一.二维数组概述：

二维数组就是元素为1维数组的数组，二维数组其实就是每一个元素为一维数组的数组

对于二维数组的声明有如下：
int[][] arr;
String[][] students;

二.二维数组的初始化：

Java中的数组必须先初始化,然后才能使用，所谓初始化：就是为数组中的数组元素分配内存空间，并为每个数组元素赋值
其中在之前有介绍过对于一维数组的初始化有动态初始化和静态初始化两种方法，同样在二维数组中也有动态初始化和静态初始化两种方法：
但是首先在初始化之前需要注意：
不管静态初始化还是动态初始化，第一维的长度必须确定！

1.动态初始化二维数组：

具体格式：
数据类型[][] 变量名 = new 数据类型[m][n]
m表示这个二维数组有多少个一维数组 必须写上
n表示每一个一维数组的元素个数 可选

举例:
int[][] arr = new int[3][2];
定义了一个二维数组arr
这个二维数组有3个一维数组，名称是arr[0],arr[1],arr[2]
每个一维数组有2个元素，可以通过arr[m][n]来获取
表示获取第m+1个一维数组的第n+1个元素

对于上面的格式还有两种定义格式供参考：

(1) 数据类型 数组名[][] = new 数据类型[m][n]
(2) 数据类型[] 数组名[] = new 数据类型[m][n]
但是这两种格式仅仅是满足定义语法，在实际中不建议

其次是初始化中的注意事项，注意下面定义的区别之处：

• int[] x,y[];
  这句话定义了两个数组 一个是一维数组x 一个是二维数组y，所以不建议将两个二维数组的初始化放在一句话中，建议将上面的初始化定义写成如下格式：

x=new int[3];
y=new int[3][]; //3只是假定了一个长度

2.静态初始化二维数组：

具体格式：
语法格式：
数组名 = new 元素的数据类型[][]{{元素1，元素2…},{元素1，元素2…}…}
当声明与静态初始化同时进行，可以简写：
元素的数据类型[][] 数组名 = {{元素1，元素2…},{元素1，元素2…}…};
即省略等号后面的new和数据类型

举例：
int mark=new int{{100,200},{10,59,60},{50,3,555,666}}
String days={{“4月1日”},{“10月1日”,“6月1日”},{“大年30”}}

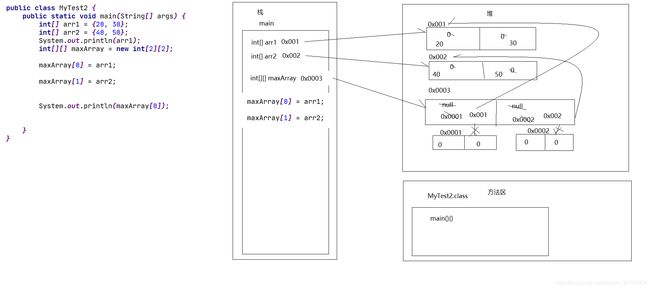
3.初始化数组的内存演示：

[1]二维数组格式1的内存图解:

public class MyTest1 {
    public static void main(String[] args) {
        //动态初始化，定义二维数组
        int[][] arr = new int[3][2];

        System.out.println(arr[0]);
        System.out.println(arr[0][0]);//0
        System.out.println(arr[0][1]);//0

        System.out.println(arr[1]);
        arr[1][0] = 10;
        arr[1][1] = 20;
        System.out.println(arr[1][0]);
        System.out.println(arr[1][1]);

        System.out.println(arr[2]);

        System.out.println(arr[2][0]);
        System.out.println(arr[2][1]);
    }
}

[2]二维数组格式2的内存图解:

public class MyTest2 {
    public static void main(String[] args) {
        int[] arr1 = {20, 30};
        arr1[0] = 100;
        arr1[1] = 200;
        int[] arr2 = {40, 50};
        System.out.println(arr1);
        int[][] maxArray = new int[2][2];

        maxArray[0] = arr1;
        maxArray[1] = arr2;
        maxArray[0][1] = 85;
        System.out.println(maxArray[0]);

        System.out.println(maxArray[0][0]);//100
        System.out.println(maxArray[0][1]);//85
    }
}

[3]二维数组格式3的内存图解:

public class MyTest3 {
    public static void main(String[] args) {
        //如果第二中括号不写长度，就不会帮你初始化一维数组
        //如果第二中括号你写了长度，就会帮你初始化二维数组中的一维数组
        int[][] maxArray = new int[2][];
        maxArray[0] = new int[2];
        maxArray[1] = new int[6];
        System.out.println(maxArray[0]);
        System.out.println(maxArray[1]);
    }
}

三.二维数组的遍历：

算法代码：

package zjl.westos;

public class ArrayErWei1 {
    //遍历二维数组
    public static void main(String[] args) {
        int arr[][]={{100,200,300},{10,20,30},{50,70,90}};
        for (int i = 0; i < arr.length; i++) {
            for (int j = 0; j < arr[i].length; j++) {
                System.out.print(arr[i][j]+" ");
            }
            System.out.println();
        }
    }
}

运行截图：

四.数组练习题总汇：

1.输出季度总额：

题干：

	需求：公司年销售额求和
	某公司按照季度和月份统计的数据如下：单位(万元)
	第一季度：22,66,44
	第二季度：77,33,88
	第三季度：25,45,65
	第四季度：11,66,99

解题思路： 对于上面的数据只需要存储到二维数组中，并遍历二维数组中的元素就可以得到正确答案
解题代码：

package zjl.westos;
import java.util.Scanner;

public class Question$SeasonSold {
    /*Question A:案例演示
	需求：公司年销售额求和
	某公司按照季度和月份统计的数据如下：单位(万元)
	第一季度：22,66,44
	第二季度：77,33,88
	第三季度：25,45,65
	第四季度：11,66,99*/
    public static void main(String[] args) {
        //静态初始化二维数组：
        int[][] sale={{22,66,44},{77,33,88},{25,45,65},{11,66,99}};
        int sum=0;
        for (int i = 0; i < sale.length; i++) {
            for (int j = 0; j < sale[i].length; j++) {
                sum+=sale[i][j];
            }
        }
        System.out.println("所有季度的营业额总和是："+sum);

        //动态初始化二维数组：
        int[][] sold=new int[4][3];
        int sumplus=0;
        Scanner input=new Scanner(System.in);
        System.out.println("请输入所有季度销售额：");
        for (int i = 0; i < 4; i++) {
            for (int j = 0; j < 3; j++) {
                sold[i][j]=input.nextInt();
            }
        }
        for (int i = 0; i < 4; i++) {
            for (int j = 0; j < 3; j++) {
                sumplus+=sold[i][j];
            }
        }
        System.out.println("总和是："+sumplus);
    }
}

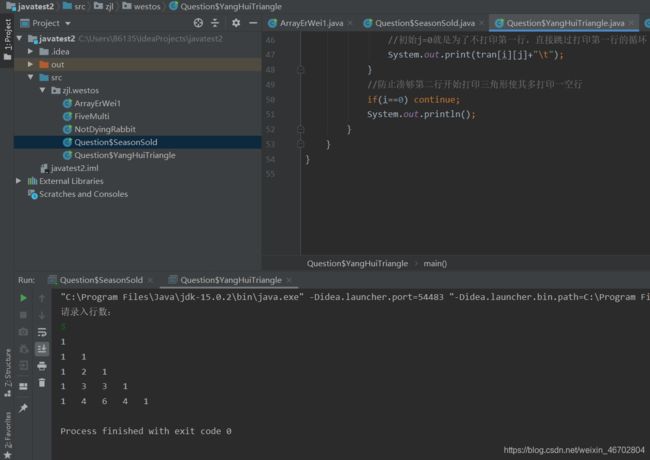
2.打印杨辉三角：

题干：

需求：打印杨辉三角形(行数可以键盘录入)

		1
		1 1	
		1 2 1
		1 3 3 1
		1 4 6 4 1 
		1 5 10 10 5 1

解题思路：

• 分析：看这种图像的规律：
  (1) 任何一行的第一列和最后一列都是1
  (2) 从第三行开始，每一个数据是它上一行的前一列和它上一行的本列之和
• 步骤：
  (1) 首先定义一个二维数组。行数如果是n，我们把列数也先定义为n，这个n的数据来自于键盘录入
  (2) 给这个二维数组任何一行的第一列和最后一列赋值为1
  (3) 按照规律给其他元素赋值
  (4) 从第三行开始，每一个数据是它上一行的前一列和它上一行的本列之和
  (5) 遍历这个二维数组。
  解题代码：

package zjl.westos;
import java.util.Scanner;

public class Question$YangHuiTriangle {
    /*B:需求：打印杨辉三角形(行数可以键盘录入)

		1
		1 1
		1 2 1
		1 3 3 1
		1 4 6 4 1
		1 5 10 10 5 1*/
    /*
    规律：
    分析：看这种图像的规律
	A:任何一行的第一列和最后一列都是1
	B:从第三行开始，每一个数据是它上一行的前一列和它上一行的本列之和
    */
    public static void main(String[] args) {
        Scanner input=new Scanner(System.in);
        System.out.println("请录入行数：");
        int line=input.nextInt()+1;
        //此处+1的作用是下面的循环进行打印时会从第二行开始
        int[][] tran=new int[line][line];

        //从第二行开始，每一行的第一个元素都是1，且每一行对应元素是它上一行的前一列和它上一行的本列之和
        for (int i = 0; i < line; i++) {
            tran[i][0]=1;
            for (int j = 1; j < i; j++) {
                tran[i][j]=tran[i-1][j-1]+tran[i-1][j];
            }
        }

        /*
        实际上的二维数组构建如下：
        从第二行开始进行相加的操作
        1
        1 1
        1 2 1
        所以在打印时要打印每行中三角形前的元素并且不打印第一行
        */

        //打印杨辉三角
        for (int i = 0; i < line; i++) {
            for (int j = 0; j < i; j++) {
                //初始j=0就是为了不打印第一行，直接跳过打印第一行的循环
                System.out.print(tran[i][j]+"\t");
            }
            //防止凑够第二行开始打印三角形使其多打印一空行
            if(i==0) continue;
            System.out.println();
        }
    }
}