离散系统冲激响应和阶跃响应

离散系统冲激响应和阶跃响应

$\text{impz()}$和$\text{stepz()}$求解离散系统的单位冲激响应和阶跃响应

$\text{impz()}$和$\text{stepz()}$用法

impz()

[h,t]=impz(b,a);%求解数字系统的冲激响应h
[h,t]=impz(b,a,n);%求解数字系统的冲激响应h,取样点数是n

stepz()

[h,t]=stepz(b,a);%求解数字系统的阶跃响应h
[h,t]=stepz(b,a,n);%求解数字系统的阶跃响应h,取样点数是n

例题

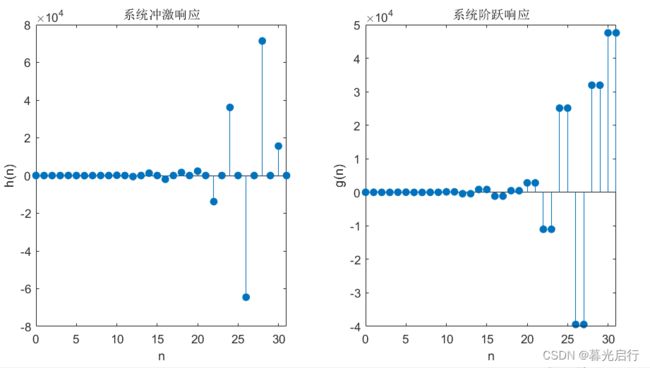
因果系统：$6y(n)+2y(n-2)=x(n)+3x(n-1)+3x(n-2)+x(n-3)$
初始条件：$y(-1)=0,x(-1)=0$
求冲激响应和阶跃响应

格式一：

%%%%%%注意归一化%%%%%%
a=[1 0 1/3 0];%对应y,由于a和b位数应该统一，所以不是a=[1 0 1/3]
b=[1/6 1/2 1/2 1/6 ];%对应x

N=32;%取N=32作图
n=0:N-1;

hn=impz(b,a,n);
gn=stepz(b,a,n);

figure('Color','w');
subplot(121),stem(n,hn,"filled");title('系统冲激响应');
ylabel('h(n)');xlabel('n');
subplot(122),stem(n,gn,"filled");title('系统阶跃响应');
ylabel('g(n)');xlabel('n');

格式二：

a=[1 0 1/3 0];%对应y,由于a和b位数应该统一，所以不是a=[1 0 1/3]
b=[1/6 1/2 1/2 1/6 ];%对应x

N=32;%取N=32作图

[hn,n]=impz(b,a,N);
[gn,n]=stepz(b,a,N);

figure('Color','w');
subplot(121),stem(n,hn,"filled");title('系统冲激响应');
ylabel('h(n)');xlabel('n');
subplot(122),stem(n,gn,"filled");title('系统阶跃响应');
ylabel('g(n)');xlabel('n');

已知$H(z)=\frac{0.1321-0.3963z^{-2}+0.3963z^{-4}-0.1321z^{-6}}{1+0.34319z^{-2}+0.60439z^{-4}+0.20407z^{-6}}$
求冲激响应和阶跃响应

a=[0.1321 0 0.3963 0 0.3963 0 -0.1321];%对应y
b=[1 0 0.34319 0 0.60439 0 0.20407];%对应x

N=32;%取N=32作图

[hn,n]=impz(b,a,N);
[gn,n]=stepz(b,a,N);

figure('Color','w');
subplot(121),stem(n,hn,"filled");title('系统冲激响应');
ylabel('h(n)');xlabel('n');
subplot(122),stem(n,gn,"filled");title('系统阶跃响应');
ylabel('g(n)');xlabel('n');

$\text{filtic()}$和$\text{filter()}$求解离散系统的单位冲激响应和阶跃响应

$\text{filtic()}$和$\text{filter()}$用法

filtic()

z=filtic(b,a,y,x)%y,x是初始状态
z=filtic(b,a,y)%x初始状态为零

filter()

y=filter(b,a,x);
[y,zf]=filter(b,a,x);%除得到结果y还得到x最终状态zf
y=filter(b,a,x,zi);%zi是x初始状态

例题

因果系统：$6y(n)+2y(n-4)=x(n)-3x(n-2)+3x(n-4)-x(n-6)$
初始条件：$y(-1)=0,x(-1)=0$
求冲激响应和阶跃响应

a=[1 0 0 0 -1/3 0 0];
b=[1/6 0 -1/2 0 1/2 0 -1/6];

N=32;
n=0:N-1;
h=zeros(size(n));
h(n==0)=1;
g=zeros(size(n));
g(n>=0)=1;

%定义初始条件
x0=0;y0=0;
zi=filtic(b,a,y0,x0);%用filter进行处理

hn=filter(b,a,h,zi);
gn=filter(b,a,g,zi);

figure('Color','w');
subplot(121)
stem(n,hn,"filled");title('单位冲激信号')
subplot(122)
stem(n,gn,"filled");title('单位阶跃信号')