第四十周:文献阅读+GAN
目录
摘要
Abstract
文献阅读:结合小波变换和主成分分析的长短期记忆神经网络深度学习在城市日需水量预测中的应用
现有问题
创新点
方法论
PCA(主要成分分析法)
DWT(离散小波变换)
DWT-PCA-LSTM模型
研究实验
实验目的
数据集
评估指标
实验设计
实验结果分析
Generative adversarial network(GAN生成对抗网络)
GAN的基本概念
GAN训练目标
生成器的训练目标
鉴别器的训练目标
GAN的目标函数
GAN的数学原理
GAN实现生成
总结
摘要
本周阅读的文献,提出了一种结合离散小波变换(DWT)和主成分分析(PCA)预处理技术的混合长短期记忆模型。其中采用DWT法消除需水量序列的噪声成分,采用主成分分析方法选择需水量影响因子中的主成分。此外,建立了两个LSTM网络,利用DWT和PCA技术的结果进行城市日需水量预测。最后通过与其他基准预测模型的比较,证明了该模型的优越性。GAN中主要包括生成器和辨别器,其中生成器对应于深度学习中的生成模型,而辨别器对应于分类模型,两者相互对抗而不断优化。GAN的训练目标是想要生成分布与真实分布越接近越好,通过辨别器优化可以衡量两者之间的JS散度,从而最小化散度值,使两个分布达到更接近。
Abstract
The literature read this week proposes a hybrid long short-term memory model that combines discrete wavelet transform (DWT) and principal component analysis (PCA) preprocessing techniques. The DWT method is used to eliminate the noise components in the water demand sequence, and the principal component analysis method is used to select the principal components in the influencing factors of water demand. In addition, two LSTM networks were established to predict urban daily water demand using the results of DWT and PCA technologies. Finally, the superiority of this model was demonstrated through comparison with other benchmark prediction models. In GAN, there are mainly generators and discriminators, where the generator corresponds to the generative model in deep learning, while the discriminator corresponds to the classification model. The two are constantly optimized against each other. The training goal of GAN is to generate a distribution that is as close as possible to the true distribution. By optimizing the discriminator, the JS divergence between the two can be measured, thereby minimizing the divergence value and making the two distributions closer.
文献阅读:结合小波变换和主成分分析的长短期记忆神经网络深度学习在城市日需水量预测中的应用
Deep learning with long short-term memory neural networks combining wavelet transform and principal component analysis for daily urban water demand forecasting
Redirecting![]() https://doi.org/10.1016/j.eswa.2021.114571
https://doi.org/10.1016/j.eswa.2021.114571
现有问题
- 统计模型只利用正态分布假设下的历史数据来寻找过去和未来值之间的联系,这导致在处理复杂和非线性时间序列时存在局限性。因此,传统的统计模型对具有随机性质的需水量序列的预测可能没有足够的准确性。
- 经典智能模型的浅层结构不能有效地处理大规模数据,在数据特征挖掘方面存在一定的局限性。
- 由于城市需水量的非平稳性和非线性受到许多因素的影响,因此单一的预测模型可能难以获得高精度的结果,以往相关研究中的模型只处理了需水量序列的单一特征,没有全面考虑时间序列的不确定性和非线性。
创新点
在混合策略和应用的启发下,,提出了一种结合离散小波变换(DWT)和主成分分析(PCA)预处理技术的混合长短期记忆模型,即基于特征提取和预测变量选择技术的混合模型来预测城市日需水量,混合策略能够利用每个个体的优点来克服彼此的局限性。
- 分别采用3σ准则和加权平均法对需水量序列异常值进行识别和平滑处理;
- 采用DWT方法去除需水量序列的噪声成分;
- 通过主成分分析识别出需水量最相关的影响变量;
- 利用DWT和PCA技术对数据进行预处理,利用DWT和PCA技术的结果经过混合LSTMs解决方案来预测城市日需水量。
方法论
PCA(主要成分分析法)
PCA的思想是将n维特征映射到k维上(k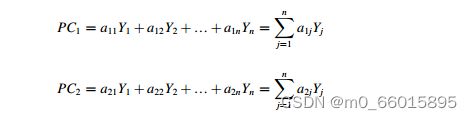
在PCA分析中,方差最大的前几个pc被称为主成分,它保留了原始变量的大部分信息,可以用来表征原始变量。通过选取前几个分量作为pc,可以降低原始变量的维数。正确的成分选择有助于预测的稳健性。
PCA实例
城市用水除了受到气候变化、社会经济条件等因素的影响,白天和一周内需水量的随机性还受到许多其他因素的影响,然而,这些变量中有许多是高度相关的,这可能会给模型的演化带来多重共线性问题。因此,本文采用主成分分析法来识别候选变量中最重要和最相关的变量。
DWT(离散小波变换)
信号低频成分常常蕴含着信号的特征,而高频成分则给出信号的细节或差别。平移、伸缩是小波变换的一个特点,因而可以在不同的频率范围,不同的时间(空间)位置对信号进行各种分析,通过这种多分辨率分析,在分析信号的低频部分的时候,只需要较大的频率分辨率和较小的时域分辨率就能够很好的体现低频的信息,而在高频部分,就需要较大的时间分辨率和较小的频率分辨率就能够很好的体现高频的信息。因此在离散小波变换中,将原始信号可以通过两个相互滤波器产生两个信号(高和低),这样便能分析信号的不同频率成分。
DWT变换的基本过程如下:
- 将原始信号进行低通滤波和高通滤波,离散变换用到了两组函数:尺度函数和小波函数,它们分别与低通滤波器和高通滤波器相对应,得到两个子信号,即近似系数和细节系数;
- 对近似系数进行递归分解,得到若干个尺度下的近似系数和细节系数;
- 通过对细节系数进行递归分解,得到若干个尺度下的细节系数;
- 重构原始信号时,将不同尺度的近似系数和细节系数进行合并,得到重构后的信号。
小波去噪的基本步骤是,将含噪信号进行多尺度小波变换,从时域变换到小波域,然后在各尺度下尽可能地提取信号的小波系数,而除去噪声的小波系数最后用小波逆变换重构信号。
水需求序列中包含的噪声特征可能构成障碍,以至于限制了对水需求时间序列过去和未来行为之间依赖关系的捕捉。为了解决这一问题,可以通过预处理阶段使原始需水量序列具有低波动性(稳定方差),离散小波变换(DWT)是连续小波变换(CWT)的离散实现,比CWT更高效。
DWT-PCA-LSTM模型
需水量序列具有较高的非线性和隐藏的季节分量,之前的研究使用前馈神经网络来学习时间序列的复杂特征,而不是使用带有反馈连接的神经网络。为了增强模型对时间序列复杂模式的学习能力,本文提出了一种新的混合模型DWT-PCA-LSTM来预测城市日需水量。
如图所示,DWT-PCA-LSTM混合模型的体系结构包括三个部分:
1、需水量数据预处理
预处理步骤需要平滑原始序列中的异常值并消除噪声成分,首先采用3σ判据区分原始需水量序列的异常值,该准则的信度范围99.73%的情况下,实际需水量值将在![]() 区间内,其中
区间内,其中![]() 和
和![]() 分别代表原始需水量序列的均值和标准差,超出该区间的需水量值视为离群值。对于序列中的异常点,采用加权平均法进行平滑处理。
分别代表原始需水量序列的均值和标准差,超出该区间的需水量值视为离群值。对于序列中的异常点,采用加权平均法进行平滑处理。
![]()
其中Et表示平滑的异常值,![]() 和
和![]() 分别表示离群值附近的加权值和历史数据。然后利用小波变换方法消除无异常值序列的噪声分量。
分别表示离群值附近的加权值和历史数据。然后利用小波变换方法消除无异常值序列的噪声分量。
2、影响因素降维
使用PCA方法消除影响变量的不重要特征,因为许多这些变量彼此高度相关,在训练模型时产生多重共线性问题。
3、利用混合模型进行需水量预测
在预测部分,为了提高预测性能,在该模型中构建了两个LSTM网络。第一个LSTM网络通过学习序列的主要特征来给出输出。因此,将降噪后的序列和主成分一起作为第一个LSTM网络的输入。第二个LSTM网络,其目的是增强模型捕捉预测结果峰值的能力。与第一个LSTM网络不同的是,第二个网络的输入由残差序列,以及得到的主成分组成。第二个LSTM的输出被视为一组人工噪声,添加到第一个LSTM的输出中。最后将两个LSTM神经网络的输出进行整合,得到最终的需水量预测。
研究实验
实验目的
通过与其他基准模型进行对比试验,验证所提出的DWT-PCA-LSTM模型对城市需水量预测的有效性。
数据集
本研究使用了中国苏州一家真实自来水厂的用水需求数据,共收集了2016年1月1日至2020年9月11日的1660个观测日需水量数据,其中前998个日数据用于模型训练,其余662个日数据用于测试。
评估指标
采用了四个标准,即平均绝对百分比误差(MAPE)、峰点MAPE (pMAPE)、解释方差得分(EVS)和相关系数(R),分别定义方程如下,其中![]() 、
、![]() 、
、![]() and
and ![]() 分别为观测值、t时刻的预测值、观测值的平均值和预测值的平均值,n为预测数据的个数。
分别为观测值、t时刻的预测值、观测值的平均值和预测值的平均值,n为预测数据的个数。
MAPE是指评估模型预测能力的无偏估计量,设置度量EVS来评估预测值与观测值之间的波动匹配程度,EVS值越高,预测效果越好,EVS最大值为1。R系数描述了观测数据与预测数据之间的线性相关关系,预测结果期望有较大的R系数值,但不大于1。
实验设计
为了确定所提出的DWT-PCA-LSTM模型相对于其他模型的有效性,必须将DWT-PCA-LSTM的预测性能与其他已知模型进行比较。采用DWT-LSTM、PCA-LSTM、LSTM、DWT-PCA-RNN、DWT-PCA-BP和DWT-PCA-SVM六种不同的模型进行比较。对于DWT-LSTM模型的输入,将pc替换为影响因素的原始数据集。PCA-LSTM模型的输入包括平滑异常值后的需水量序列和影响因素的pc。在LSTM预测模型中,将无异常值的需水量序列和全部影响因素输入到模型中。对于DWT-PCA-RNN模型,其中包含两个RNN网络,并将两个网络的输出集成以产生最终预测。采用BPTT算法实现的DWT-PCA-BP模型有一个隐藏层,包含20个隐藏节点。对于DWT-PCA-SVM模型,SVM的核函数设置为Radial Basis function,惩罚参数c设置为10。
实验结果分析
通过评价标准衡量各模型预测需水量序列的性能,从结果可以看出提出的DWT-PCA-LSTM模型优于其他预测模型,拥有最小的MAPE和pMAPE和最高的R和EVS,这表明LSTM网络在预测需水量序列方面优于其他研究算法。
实验证明,采用小波变换和主成分分析方法可以产生方差稳定、低维的高质量输入变量。同时,在DWT-PCA-LSTM模型中集成两个LSTM网络,使得预测不仅在整个预测范围内的平均误差更小,而且在峰值点的预测精度更高。
Generative adversarial network(GAN生成对抗网络)
GAN的基本概念
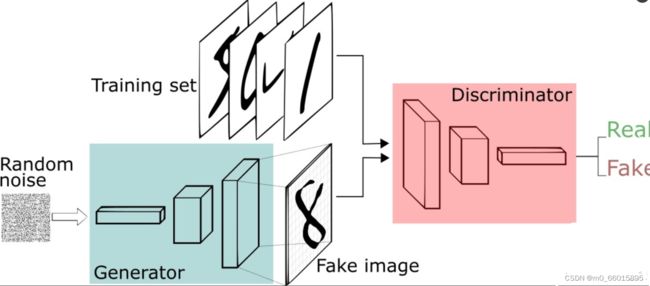
生成对抗网络其实是两个网络的组合:生成网络(Generator)负责生成模拟数据;判别网络Discriminator)负责判断输入的数据是真实的还是生成的。生成网络要不断优化自己生成的数据让判别网络判断不出来,判别器负责判断生成器生成的样本是否为真。生成器要尽可能迷惑判别器,而判别器要尽可能区分生成器生成的样本和真实样本。
生成器的输入是由高斯分布随机采样得到的噪声,通过生成器得到了生成的假样本。生成的假样本与真实样本放到一起,被随机抽取送入到判别器,由判别器去区分输入的样本是生成的假样本还是真实的样本。
在GAN的原作中,作者将生成器比喻为印假钞票的犯罪分子,判别器则类比为警察。犯罪分子努力让钞票看起来逼真,警察则不断提升对于假钞的辨识能力。二者互相博弈,随着时间的进行,都会越来越强。那么类比于图像生成任务,生成器不断生成尽可能逼真的假图像。判别器则判断图像是否是真实的图像,还是生成的图像,二者不断博弈优化。最终生成器生成的图像使得判别器完全无法判别真假。
生成器对应于深度学习中的生成模型,而辨别器对应于深度学习中的分类模型
GAN训练目标
生成器的训练目标
![]() 即Divergence,是衡量两个Distribution相似度的一个major,当Divergence的值越大就代表这两个Distribution越不像。Divergence的值越小就代表这两个Distribution越相近。
即Divergence,是衡量两个Distribution相似度的一个major,当Divergence的值越大就代表这两个Distribution越不像。Divergence的值越小就代表这两个Distribution越相近。
与普通的神经网络的训练一样,定义Loss Function,找到一组参数使得Loss的值最小。那么在Generation的训练要做的事情就是找一组Generator里面的参数(Generator是一个Network,里面也有大量的weight和bias),使得通过在这组参数下的Generator![]() 得到的
得到的![]() 与c越小越好。因此在Generation问题中我们的Loss Function就是
与c越小越好。因此在Generation问题中我们的Loss Function就是![]()
对于GAN来说,不需要知道![]() 和
和![]() 的分布,只要知道怎么从
的分布,只要知道怎么从![]() 和
和![]() 中sample东西出来,就可以算出Divergence,而
中sample东西出来,就可以算出Divergence,而![]() 和
和![]() 是可以sample的。对于真实的数据
是可以sample的。对于真实的数据![]() 从图片库里sample一些出来就可以得到了,而
从图片库里sample一些出来就可以得到了,而![]() 的sample是可以通过Generaator产生得到的。
的sample是可以通过Generaator产生得到的。
鉴别器的训练目标
通过sample就可以计算Divergence,这就需要依靠Discriminator的力量了,Discriminator 就是要尽量把从![]() 里sample的数据与从
里sample的数据与从![]() 里sample的数据分开,这其实也可以用 Binary Classifier 做,把
里sample的数据分开,这其实也可以用 Binary Classifier 做,把![]() 的sample 当作 class 1, 把
的sample 当作 class 1, 把 ![]() 的sample当作class 2,如下图所示。设计 Classifier 的目标函数
的sample当作class 2,如下图所示。设计 Classifier 的目标函数 ![]()
根据从![]() 和
和![]() 中sample出来的data训练一个Discriminator,训练的目标就是看到real data就给它高分,看到generation data就给低分,也就是要分辨一个图片是真的图还是生成的图。
中sample出来的data训练一个Discriminator,训练的目标就是看到real data就给它高分,看到generation data就给低分,也就是要分辨一个图片是真的图还是生成的图。
其实Discriminator的问题可以当作是一个Optimization的问题
训练出来的Discriminator可以去maximize Objective Function,(minimize的就叫Loss Function),因此要找一个D可以Maximize这个Objective Function。
如下图所示。设计 Classifier 的目标函数 ![]()
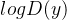 :
: 的sample 经过 Discriminator 得到的分数
的sample 经过 Discriminator 得到的分数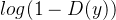 :
: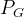 的sample 经过 Discriminator 得到的分数
的sample 经过 Discriminator 得到的分数
我们希望可以找到一个D使得![]() 越大越好,也就是说希望
越大越好,也就是说希望![]() 的值越大越好,代表给真正的Image打分越高越好。经过推导可以发现
的值越大越好,代表给真正的Image打分越高越好。经过推导可以发现![]() 的最大值与 JS divergence 有关。
的最大值与 JS divergence 有关。
下面通过例子从直观上来理解为什么Objective Function的最大值是和Divergence有关的,当![]() 和
和![]() 两组sample出来的数据之间的divergence很小的时候,Discriminator 很难分辨两者,因此打的分数不准确,则
两组sample出来的数据之间的divergence很小的时候,Discriminator 很难分辨两者,因此打的分数不准确,则![]() 的值小。反之当divergence很大的时候,Discriminator 很容易分辨两者,因此打的分数比较准确,则
的值小。反之当divergence很大的时候,Discriminator 很容易分辨两者,因此打的分数比较准确,则![]() 的值大。
的值大。
训练Discriminator的目标就是分辨出真正的Image和生成的Image,即使![]() 的值达到最大,而Generator的目标就是让生成的图片瞒过Discriminator,因此它的目标是让
的值达到最大,而Generator的目标就是让生成的图片瞒过Discriminator,因此它的目标是让![]() 的值越小越好,因此
的值越小越好,因此![]() 等式右边既有min又有max。
等式右边既有min又有max。
GAN的目标函数
对于神经网络模型,如果想要学习其参数,首先需要一个目标函数。GAN的目标函数定义为:
这个目标函数可以分为两个部分来理解:
- 判别器的优化通过
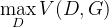 实现,其第一项
实现,其第一项![{\rm E}{x\sim{p{data}(x)}}[\log D(x)]](http://img.e-com-net.com/image/info8/201de8af9566443da09537dba77a5e47.png) 表示对于从真实数据分布
表示对于从真实数据分布 中采用的样本,其被判别器判定为真实样本概率的数学期望。对于真实数据分布 中采样的样本,其预测为正样本的概率当然是越接近1越好。因此希望最大化这一项。第二项
中采用的样本,其被判别器判定为真实样本概率的数学期望。对于真实数据分布 中采样的样本,其预测为正样本的概率当然是越接近1越好。因此希望最大化这一项。第二项![{\rm E}_{z\sim{p_z}(z)}[\log (1 - D(G(z)))]](http://img.e-com-net.com/image/info8/1b508805106a44728f7780fdfde3d1ff.png) 表示对于从噪声
表示对于从噪声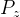 分布当中采样得到的样本,经过生成器生成之后得到的生成图片,然后送入判别器,其预测概率的负对数的期望,这个值自然是越大越好,这个值越大, 越接近0,也就代表判别器越好。
分布当中采样得到的样本,经过生成器生成之后得到的生成图片,然后送入判别器,其预测概率的负对数的期望,这个值自然是越大越好,这个值越大, 越接近0,也就代表判别器越好。 - 生成器的优化通过
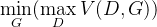 来实现。注意,生成器的目标不是
来实现。注意,生成器的目标不是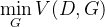 ,即生成器不是最小化判别器的目标函数,二是最小化判别器目标函数的最大值,判别器目标函数的最大值代表的是真实数据分布与生成数据分布的JS散度(详情可以参阅附录的推导),JS散度可以度量分布的相似性,两个分布越接近,JS散度越小。
,即生成器不是最小化判别器的目标函数,二是最小化判别器目标函数的最大值,判别器目标函数的最大值代表的是真实数据分布与生成数据分布的JS散度(详情可以参阅附录的推导),JS散度可以度量分布的相似性,两个分布越接近,JS散度越小。
GAN的数学原理
相关数学理论
GAN目标函数优化
数学证明为什么
时,目标函数达到最优。
所以说对鉴别器D的优化就是在求
与
的JS散度
,对
其实G的优化就是在缩小
与
的JS散度。
GAN实现生成
使用对抗式生成网络基于MNIST的手写数字数据集实现自动生成手写数字,基于pytrch实现。
数据集来源:Kaggle数据集
模型代码
import torch
import torch.nn as nn
# 生成器(基于线性层)
class G_net_linear(nn.Module):
def __init__(self):
super(G_net_linear, self).__init__()
#序列容器,用于搭建神经网络的模块被按照被传入构造器的顺序添加到nn.Sequential()容器中
#利用nn.Sequential() 自定义自己的网络层
self.gen = nn.Sequential(
nn.Linear(256, 256), #线性层
nn.BatchNorm1d(256), #批归一化
nn.Dropout(0.5), #随机丢弃层(防止过拟合)
nn.LeakyReLU(0.2), #LeakyReLU激活函数(它在非负数部分保持线性,而在负数部分引
#入一个小的斜率(通常是一个小的正数),以防止梯度消失问题)
nn.Linear(256, 512),
nn.BatchNorm1d(512),
nn.Dropout(0.5),
nn.LeakyReLU(0.2),
nn.Linear(512, 1024),
nn.BatchNorm1d(1024),
nn.Dropout(0.5),
nn.LeakyReLU(0.2),
#总共三大层,每层由线性模型、批归一化、丢弃层和激活函数层组成
nn.Linear(1024, 784),
# 将输出约束到[-1,1]
nn.Tanh()
)
def forward(self, img_seeds):
output = self.gen(img_seeds)
# 将线性数据重组为二维图片
output = output.view(-1, 1, 28, 28)
return output
# 根据生成器的配置返回对应的模型
def get_G_model(from_old_model, device, model_path, G_type):
model = G_net_linear()
# 从磁盘加载之前保存的模型参数
if from_old_model:
model.load_state_dict(torch.load(model_path))
# 将模型加载到用于运算的设备的内存
model = model.to(device)
return model
# 判别器
class D_net(nn.Module):
def __init__(self):
super(D_net, self).__init__()
self.features = nn.Sequential(
#由两大模块组成,每个模块包括卷积层、批归一化层、激活函数RuLU层
nn.Conv2d(1, 32, kernel_size=3), #卷积层,用于实现二维卷积操作
#1个输入通道(与所输入的图片通道相同)32个卷积核(将要输出的卷积通道数) 3*3大小
nn.BatchNorm2d(32),
nn.LeakyReLU(0.2),
nn.Conv2d(32, 64, kernel_size=3),
#32个输入通道(与所输入的图片通道相同)64个卷积核(将要输出的卷积通道数)3*3大小
nn.BatchNorm2d(64),
nn.LeakyReLU(0.2),
)
#分类器,由线性层和RuLU层组成,最后通过sigmoid得到概率值
self.classifier = nn.Sequential(
nn.Linear(36864, 1024),
nn.LeakyReLU(0.2),
nn.Linear(1024, 1024),
nn.LeakyReLU(0.2),
nn.Linear(1024, 1),
nn.Sigmoid(),
)
def forward(self, img):
# 提取特征
features = self.features(img)
# 展平二维矩阵
features = features.view(features.shape[0],-1)
# 使用线性层分类
output = self.classifier(features)
return output
# 返回判别器的模型
def get_D_model(from_old_model, device, model_path):
model = D_net()
# 从磁盘加载之前保存的模型参数
if from_old_model:
model.load_state_dict(torch.load(model_path))
# 将模型加载到用于运算的设备的内存
model = model.to(device)
return model
训练代码
import pandas as pd
from torch.utils.data import Dataset, DataLoader
import time
from torch.optim import AdamW
import numpy as np
from model import *
from torchvision import transforms
from torchvision.utils import save_image
import random
from torch.autograd import Variable
import os
class config:
# 设置种子数,配置是否要固定种子数
seed = 26
use_seed = True
# 配置是否要从磁盘加载之前保存的模型参数继续训练
from_old_model = False
# 运行多少个epoch之后停止
epochs = 100
# 配置batch size
batchSize = 64
# 配置喂入生成器的随机正态分布种子数有多少维
img_seed_dim = 256
# 有多大概率在训练判别器D时交换正确图片的标签和伪造图片的标签
D_train_label_exchange = 0.05
# 保存模型参数文件的路径
G_model_path = "G_model.pth"
D_model_path = "D_model.pth"
# 基于纯线性层的生成器
G_type = "Linear"
# 损失函数
# 使用二分类交叉熵损失函数
criterion = nn.BCELoss()
# 使用均方差损失函数,经过测试也能训练,但是要跑更多epoch才能看到效果
# criterion = nn.MSELoss()
# 数据集来源
data_path = "MNIST.csv"
# 输出图片的文件夹路径
output_path = "output_images/"
# 固定随机数种子
def seed_all(seed):
random.seed(seed)
torch.manual_seed(seed)
torch.cuda.manual_seed(seed)
torch.cuda.manual_seed_all(seed)
torch.backends.cudnn.deterministic = True
if config.use_seed:
seed_all(seed=config.seed)
class Digit_train_Dataset(Dataset):
def __init__(self, data_csv, transform):
# 因为数据集很小,所以将所有数据保存在内存中
self.imgs = []
for index in range(len(data_csv)):
# 从csv文件中读取像素数据
img = np.array(data_csv.iloc[index, 1:785]).astype("uint8")
# 将一维数据重新重组为二维的手写体图片
img = img.reshape((28, 28))
# 将图片的数据缩放到[-1,1]的区间内,并转换为tensor类型
img = transform(img)
# 将图片保存到内存中
self.imgs.append(img)
def __getitem__(self, index):
# 按照索引取出内存中已经预处理完成的图片
return self.imgs[index]
def __len__(self):
return len(self.imgs)
def main():
# 如果可以使用GPU运算,则使用GPU,否则使用CPU
device = torch.device('cuda:0' if torch.cuda.is_available() else 'cpu')
print("Use " + str(device))
# 图片预处理的方法
img_transform = transforms.Compose([
# 将图片转换为tensor类型并缩放到[0,1]的区间内
transforms.ToTensor(),
# 将图片再缩放到[-1.1]的区间内
transforms.Normalize((0.5,), (0.5,)),
])
# 创建输出文件夹
if not os.path.exists(config.output_path):
os.mkdir(config.output_path)
# 创建dataset
mnist_dataset = Digit_train_Dataset(pd.read_csv("MNIST.csv"), transform=img_transform)
# 创建dataloader
mnist_loader = DataLoader(dataset=mnist_dataset, batch_size=config.batchSize, shuffle=True)
# 从model中获取判别器D和生成器G的网络模型
G_model = get_G_model(config.from_old_model, device, config.G_model_path, config.G_type)
D_model = get_D_model(config.from_old_model, device, config.D_model_path)
# 定义G和D的优化器,此处使用AdamW优化器,学习率为1e-4
G_optimizer = AdamW(G_model.parameters(), lr=1e-4, weight_decay=1e-6)
D_optimizer = AdamW(D_model.parameters(), lr=1e-4, weight_decay=1e-6)
# 损失函数
criterion = config.criterion
# 记录训练时间
train_start = time.time()
# 开始训练的每一个epoch
for epoch in range(config.epochs):
print("start epoch "+str(epoch+1)+":")
# 定义一些变量用于记录进度和损失
batch_num = len(mnist_loader)
D_loss_sum = 0
G_loss_sum = 0
count = 0
# 从dataloader中提取数据
for index, images in enumerate(mnist_loader):
count += 1
# 将图片放入运算设备的内存
images = images.to(device)
# 定义真标签,使用标签平滑的策略,生成0.9到1之间的随机数作为真实标签
real_labels = (1 - torch.rand(config.batchSize, 1)/10).to(device)
# 定义假标签,单向平滑,因此不对生成器标签进行平滑处理,全0
fake_labels = Variable(torch.zeros(config.batchSize, 1)).to(device)
# 将随机的初始数据喂入生成器生成假图像
img_seeds = torch.randn(config.batchSize, config.img_seed_dim).to(device)
fake_images = G_model(img_seeds)
# 记录真假标签是否被交换过
exchange_labels = False
# 有一定概率在训练判别器时交换label
if random.uniform(0, 1) < config.D_train_label_exchange:
real_labels, fake_labels = fake_labels, real_labels
exchange_labels = True
# 训练判断器D
D_optimizer.zero_grad()
# 用真样本输入判别器
real_output = D_model(images)
# 对于数据集末尾的数据,长度不够一个batch size时需要去除过长的真实标签
if len(real_labels) > len(real_output):
D_loss_real = criterion(real_output, real_labels[:len(real_output)])
else:
D_loss_real = criterion(real_output, real_labels)
# 用假样本输入判别器
fake_output = D_model(fake_images)
D_loss_fake = criterion(fake_output, fake_labels)
# 将真样本与假样本损失相加,得到判别器的损失
D_loss = D_loss_real + D_loss_fake
D_loss_sum += D_loss.item()
# 重置优化器
D_optimizer.zero_grad()
# 用损失更新判别器D
D_loss.backward()
D_optimizer.step()
# 如果之前交换过标签,此时再换回来
if exchange_labels:
real_labels, fake_labels = fake_labels, real_labels
# 训练生成器G
# 将随机种子数喂入生成器G生成假数据
img_seeds = torch.randn(config.batchSize, config.img_seed_dim).to(device)
fake_images = G_model(img_seeds)
# 将假数据输入判别器
fake_output = D_model(fake_images)
# 将假数据的判别结果与真实标签对比得到损失
G_loss = criterion(fake_output, real_labels)
G_loss_sum += G_loss.item()
# 重置优化器
G_optimizer.zero_grad()
# 利用损失更新生成器G
G_loss.backward()
G_optimizer.step()
# 打印程序工作进度
if (index + 1) % 200 == 0:
print("Epoch: %2d, Batch: %4d / %4d" % (epoch + 1, index + 1, batch_num))
# 在每个epoch结束时保存模型参数到磁盘文件
torch.save(G_model.state_dict(), config.G_model_path)
torch.save(D_model.state_dict(), config.D_model_path)
# 在每个epoch结束时输出一组生成器产生的图片到输出文件夹
img_seeds = torch.randn(config.batchSize, config.img_seed_dim).to(device)
fake_images = G_model(img_seeds).cuda().data
# 将假图像缩放到[0,1]的区间
fake_images = 0.5 * (fake_images + 1)
fake_images = fake_images.clamp(0, 1)
# 连接所有生成的图片然后用自带的save_image()函数输出到磁盘文件
fake_images = fake_images.view(-1, 1, 28, 28)
save_image(fake_images, config.output_path+str(epoch+1)+'.png')
# 运行结束
print("Done.")
if __name__ == '__main__':
main()
下图分别为第5次epoch和25次epoch的结果
总结
纵观整个GAN,最初是想计算![]() 与
与![]() 的相似度,但是不能直接计算 ,因此借助一个分类器D,通过
的相似度,但是不能直接计算 ,因此借助一个分类器D,通过![]() 求出一个最佳的
求出一个最佳的![]() 后,
后,![]() 就是在衡量
就是在衡量 ![]() 与
与![]() 的JS 散度,然后,最小化这个散度值,更新一次
的JS 散度,然后,最小化这个散度值,更新一次![]() ,有了新的
,有了新的![]() 后,进一步求出最佳的
后,进一步求出最佳的![]() ,然后重复上面的步骤。
,然后重复上面的步骤。




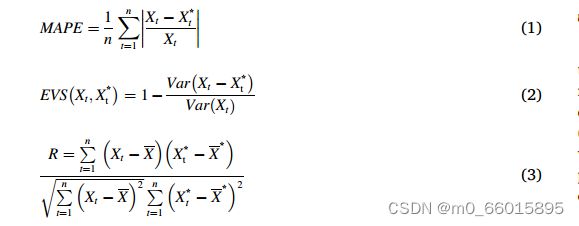






![\mathop {\min }\limits_G \mathop {\max }\limits_D V(D,G)={\rm E}{x\sim{p{data}(x)}}log D(x)+{\rm E}_{z\sim{p_z}(z)}[log(1-D(G(z)))]](http://img.e-com-net.com/image/info8/a2a24bf85ae640e2baceba348ffd9629.png)




