PKU 2528 POJ 2528 Mayor's posters ( 线段树+离散化 ) ACM 2528 IN PKU
MiYu原创, 转帖请注明 : 转载自 ______________白白の屋 
题目地址 :
http://poj.org/problem?id=2528
题目描述:
Mayor's posters
| Time Limit: 1000MS | Memory Limit: 65536K | |
| Total Submissions: 15722 | Accepted: 4444 |
Description
The citizens of Bytetown, AB, could not stand that the candidates in the mayoral election campaign have been placing their electoral posters at all places at their whim. The city council has finally decided to build an electoral wall for placing the posters and introduce the following rules:
They have built a wall 10000000 bytes long (such that there is enough place for all candidates). When the electoral campaign was restarted, the candidates were placing their posters on the wall and their posters differed widely in width. Moreover, the candidates started placing their posters on wall segments already occupied by other posters. Everyone in Bytetown was curious whose posters will be visible (entirely or in part) on the last day before elections.
Your task is to find the number of visible posters when all the posters are placed given the information about posters' size, their place and order of placement on the electoral wall.
- Every candidate can place exactly one poster on the wall.
- All posters are of the same height equal to the height of the wall; the width of a poster can be any integer number of bytes (byte is the unit of length in Bytetown).
- The wall is divided into segments and the width of each segment is one byte.
- Each poster must completely cover a contiguous number of wall segments.
They have built a wall 10000000 bytes long (such that there is enough place for all candidates). When the electoral campaign was restarted, the candidates were placing their posters on the wall and their posters differed widely in width. Moreover, the candidates started placing their posters on wall segments already occupied by other posters. Everyone in Bytetown was curious whose posters will be visible (entirely or in part) on the last day before elections.
Your task is to find the number of visible posters when all the posters are placed given the information about posters' size, their place and order of placement on the electoral wall.
Input
The first line of input contains a number c giving the number of cases that follow. The first line of data for a single case contains number 1 <= n <= 10000. The subsequent n lines describe the posters in the order in which they were placed. The i-th line among the n lines contains two integer numbers l
i and ri which are the number of the wall segment occupied by the left end and the right end of the i-th poster, respectively. We know that for each 1 <= i <= n, 1 <= l
i <= ri <= 10000000. After the i-th poster is placed, it entirely covers all wall segments numbered l
i, l
i+1 ,... , ri.
Output
For each input data set print the number of visible posters after all the posters are placed.
The picture below illustrates the case of the sample input.
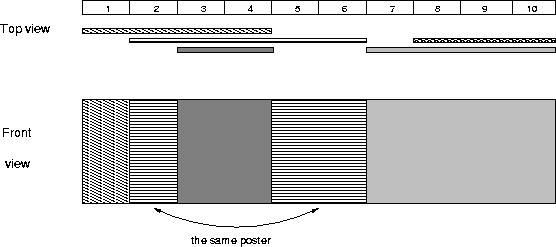
The picture below illustrates the case of the sample input.

Sample Input
1 5 1 4 2 6 8 10 3 4 7 10
Sample Output
4
题目分析 :
 代码
代码
/*
线段树 + 离散化
好像记得暑假做 树状数组的时候 做过一个离散化的题目, 当时是用2分查询
离散节点标记的, 速度还是可以的, 不过那时对离散化也没有什么概念, 大
概是没怎么接触, 今天做了这道题目的时候, 也算是明白了 离散化 的基本
意思,因为 题目的 数据范围很大 , 1- 10000000,直接线段树的话, 先不说
内存会不会爆, 这么大的范围估计也是 TLE了.
仔细读题, 可以看到 1<= N <= 10000, 也就是说 最多只有 10000个点, 如果
每个点都不同, 那么最多也只有 20000 个数据, 那么离散后的 范围就相当小;
离散化 的大概思路 : 比如说给你一组 数据 1 4 1000 100000, 如果直接
开线段, 显然是浪费, 那么我们只要 进行 映射 :
1 1
4 2
1000 3
100000 4
接下来 我们只要对 1 2 3 4 建立线段树就行了 只需要
[1,4]的区间
*/
/*
Mail to : [email protected]
Link : http://www.cnblogs.com/MiYu || http://www.cppblog.com/MiYu
Author By : MiYu
Test : 1
Complier : g++ mingw32-3.4.2
Program : 2528
Doc Name : Mayor's posters
*/
// #pragma warning( disable:4789 )
#include < iostream >
#include < fstream >
#include < sstream >
#include < algorithm >
#include < string >
#include < set >
#include < map >
#include < utility >
#include < queue >
#include < stack >
#include < list >
#include < vector >
#include < cstdio >
#include < cstdlib >
#include < cstring >
#include < cmath >
#include < ctime >
using namespace std;
int T, N, x, y;
map < int , int > mp;
set < int > st;
map < int , int > ::iterator beg, end;
struct segtree {
int left, right,cov;
int mid () { return (left + right) >> 1 ; }
}seg[ 80010 ];
struct P { // 节点数据
int left, right;
}pp[ 10010 ];
void creat ( int x, int y, int rt = 1 ) {
seg[rt].left = x;
seg[rt].right = y;
seg[rt].cov = 0 ;
if ( x == y ) return ;
int mid = seg[rt].mid();
creat ( x, mid, rt << 1 );
creat ( mid + 1 , y, rt << 1 | 1 );
}
void insert ( int x, int y, int flag, int rt = 1 ) {
// 如果线段被覆盖, 直接标记, 返回
if ( seg[rt].left == x && seg[rt].right == y ) {
seg[rt].cov = flag;
return ;
}
int LL = rt << 1 , RR = rt << 1 | 1 , mid = seg[rt].mid();
if ( seg[rt].cov != - 1 ) {
// 如果线段是被覆盖的 , 标记下传, 同时自身标记-1,表示有多个标记
seg[LL].cov = seg[RR].cov = seg[rt].cov;
seg[rt].cov = - 1 ;
}
// 递归 插入
if ( y <= mid ) insert ( x, y, flag, LL );
else if ( x > mid ) insert ( x, y, flag, RR );
else {
insert ( x, mid, flag, LL );
insert ( mid + 1 , y, flag, RR );
}
}
void query ( int x, int y, int rt = 1 ) {
// 线段被覆盖 , 将覆盖标记 放入 set
if ( seg[rt].cov != - 1 && seg[rt].left == x && seg[rt].right == y ) {
st.insert ( seg[rt].cov );
return ;
} else { // 递归查询
int LL = rt << 1 , RR = rt << 1 | 1 , mid = seg[rt].mid();
if ( y <= mid ) query ( x, y, rt << 1 );
else if ( x > mid ) query ( x, y, rt << 1 | 1 );
else {
query ( x, mid, LL );
query ( mid + 1 , y, RR );
}
}
}
void print () {
for ( set < int > ::iterator it = st.begin(); it != st.end(); ++ it )
cout << * it << endl;
}
int main ()
{
scanf ( " %d " , & T );
creat ( 1 , 20010 );
while ( T -- ) {
mp.clear();
st.clear ();
scanf ( " %d " , & N );
for ( int i = 1 ; i <= N; ++ i ) {
scanf ( " %d%d " , & pp[i].left, & pp[i].right );
// map 去重
mp[pp[i].left] = 88 ; mp[pp[i].right] = 88 ;
}
beg = mp.begin(), end = mp.end();
// 因为map 已经自动排序了,所以直接从 1 --> N 开始标记, 离散化
for ( int i = 1 ;beg != end; ++ beg, ++ i ) {
beg -> second = i;
}
// 因为线段树已经建立好了, 所以没必要每次都重建一次, 只要插入一条
// 覆盖所有区间的 底板 就行了
insert ( 1 , N * 2 , 0 );
for ( int i = 1 ; i <= N; ++ i ) {
// 用离散后的标记 插入 线段
insert ( mp[pp[i].left], mp[pp[i].right], i );
}
query ( 1 , N * 2 );
// print();
int cnt = st.size();
if ( * st.begin() == 0 ) -- cnt;
printf ( " %d\n " , cnt );
}
return 0 ;
}
线段树 + 离散化
好像记得暑假做 树状数组的时候 做过一个离散化的题目, 当时是用2分查询
离散节点标记的, 速度还是可以的, 不过那时对离散化也没有什么概念, 大
概是没怎么接触, 今天做了这道题目的时候, 也算是明白了 离散化 的基本
意思,因为 题目的 数据范围很大 , 1- 10000000,直接线段树的话, 先不说
内存会不会爆, 这么大的范围估计也是 TLE了.
仔细读题, 可以看到 1<= N <= 10000, 也就是说 最多只有 10000个点, 如果
每个点都不同, 那么最多也只有 20000 个数据, 那么离散后的 范围就相当小;
离散化 的大概思路 : 比如说给你一组 数据 1 4 1000 100000, 如果直接
开线段, 显然是浪费, 那么我们只要 进行 映射 :
1 1
4 2
1000 3
100000 4
接下来 我们只要对 1 2 3 4 建立线段树就行了 只需要
[1,4]的区间
*/
/*
Mail to : [email protected]
Link : http://www.cnblogs.com/MiYu || http://www.cppblog.com/MiYu
Author By : MiYu
Test : 1
Complier : g++ mingw32-3.4.2
Program : 2528
Doc Name : Mayor's posters
*/
// #pragma warning( disable:4789 )
#include < iostream >
#include < fstream >
#include < sstream >
#include < algorithm >
#include < string >
#include < set >
#include < map >
#include < utility >
#include < queue >
#include < stack >
#include < list >
#include < vector >
#include < cstdio >
#include < cstdlib >
#include < cstring >
#include < cmath >
#include < ctime >
using namespace std;
int T, N, x, y;
map < int , int > mp;
set < int > st;
map < int , int > ::iterator beg, end;
struct segtree {
int left, right,cov;
int mid () { return (left + right) >> 1 ; }
}seg[ 80010 ];
struct P { // 节点数据
int left, right;
}pp[ 10010 ];
void creat ( int x, int y, int rt = 1 ) {
seg[rt].left = x;
seg[rt].right = y;
seg[rt].cov = 0 ;
if ( x == y ) return ;
int mid = seg[rt].mid();
creat ( x, mid, rt << 1 );
creat ( mid + 1 , y, rt << 1 | 1 );
}
void insert ( int x, int y, int flag, int rt = 1 ) {
// 如果线段被覆盖, 直接标记, 返回
if ( seg[rt].left == x && seg[rt].right == y ) {
seg[rt].cov = flag;
return ;
}
int LL = rt << 1 , RR = rt << 1 | 1 , mid = seg[rt].mid();
if ( seg[rt].cov != - 1 ) {
// 如果线段是被覆盖的 , 标记下传, 同时自身标记-1,表示有多个标记
seg[LL].cov = seg[RR].cov = seg[rt].cov;
seg[rt].cov = - 1 ;
}
// 递归 插入
if ( y <= mid ) insert ( x, y, flag, LL );
else if ( x > mid ) insert ( x, y, flag, RR );
else {
insert ( x, mid, flag, LL );
insert ( mid + 1 , y, flag, RR );
}
}
void query ( int x, int y, int rt = 1 ) {
// 线段被覆盖 , 将覆盖标记 放入 set
if ( seg[rt].cov != - 1 && seg[rt].left == x && seg[rt].right == y ) {
st.insert ( seg[rt].cov );
return ;
} else { // 递归查询
int LL = rt << 1 , RR = rt << 1 | 1 , mid = seg[rt].mid();
if ( y <= mid ) query ( x, y, rt << 1 );
else if ( x > mid ) query ( x, y, rt << 1 | 1 );
else {
query ( x, mid, LL );
query ( mid + 1 , y, RR );
}
}
}
void print () {
for ( set < int > ::iterator it = st.begin(); it != st.end(); ++ it )
cout << * it << endl;
}
int main ()
{
scanf ( " %d " , & T );
creat ( 1 , 20010 );
while ( T -- ) {
mp.clear();
st.clear ();
scanf ( " %d " , & N );
for ( int i = 1 ; i <= N; ++ i ) {
scanf ( " %d%d " , & pp[i].left, & pp[i].right );
// map 去重
mp[pp[i].left] = 88 ; mp[pp[i].right] = 88 ;
}
beg = mp.begin(), end = mp.end();
// 因为map 已经自动排序了,所以直接从 1 --> N 开始标记, 离散化
for ( int i = 1 ;beg != end; ++ beg, ++ i ) {
beg -> second = i;
}
// 因为线段树已经建立好了, 所以没必要每次都重建一次, 只要插入一条
// 覆盖所有区间的 底板 就行了
insert ( 1 , N * 2 , 0 );
for ( int i = 1 ; i <= N; ++ i ) {
// 用离散后的标记 插入 线段
insert ( mp[pp[i].left], mp[pp[i].right], i );
}
query ( 1 , N * 2 );
// print();
int cnt = st.size();
if ( * st.begin() == 0 ) -- cnt;
printf ( " %d\n " , cnt );
}
return 0 ;
}
