【数据结构】线性表
一、线性表的定义和基本操作
1、线性表的定义和基本操作
说明:定义注重的是逻辑结构,而基本操作注重运算。
注:数据结构的三要素——逻辑结构、数据的运算、存储结构(物理结构)。
存储结构不同,运算的实现方式也不同。
2、线性表的定义
线性表是具有相同数据类型的n(n>=0)个数据元素的有限序列,其中n为表长,当n=0时线性表为一个空表。
L=(a1,a2,…,ai-1,ai,ai+1,…,an)
注意:
-
线性表中元素个数n,称为线性表的长度。当n=0时,为空表。
-
a1是唯一的“第一个”数据元素,称为表头元素;an是唯一的“最后一个”数据元素,称为表尾元素。
-
ai-1为ai的直接前驱,ai+1为ai的直接后继。
-
位序从1开始,区别于数组下标从0开始。
特点:
-
表中元素的个数是有限的。
-
表中元素的数据类型都相同。意味着每一个元素占用相同大小的空间。
-
表中元素具有逻辑上的顺序性,在序列中各元素排序有其先后顺序。
3、线性表的基本操作
InitList(&L):初始化表。构造一个空的线性表L,分配内存空间。
DestroyList(&L):销毁操作。销毁线性表,并释放线性表L所占用的内存空间。
ListInsert(&L,i,e):插入操作。在表L中的第i个位置上插入指定元素e。
ListDelete(&L,i,&e):删除操作。删除表L中第i个位置的元素,并用e返回删除元素的值。
LocateElem(L,e):按值查找。在表L中查找具体给定关键字e的元素。
GetElem(L,i):按位查找。获取表L中第i个位置的元素的值。
Length(L):求表长。返回线性表L的长度,即L中数据元素的个数。
PrintList(L):输出操作。按前后顺序输出线性表L的所有元素值。
Empty(L):判空操作。若L为空表,返回true,否则返回false。
说明:
-
在后面的实战中,就会使用这些函数做具体的操作。
-
修改之前需要先查找。
-
&符号的使用。
4、小结
二、线性表的顺序表示
1、顺序表的定义
顺序表:用顺序存储的方式实现线性表。
顺序存储:把逻辑上相邻的元素存储在物理位置上也相邻的存储单元中,元素之间的关系由存储单元的邻接关系来体现。
2、优缺点比较
3、顺序表的实现--静态分配
说明:
-
对于图中的第2步,如果不初始化,则有可能出现脏数据的情况。
-
静态分配的方式,顺序表从一开始就确定了长度,无法改变。
-
如果一开始分配的内存较大,则有可能出现浪费内存的情况。
4、线性表的实现--动态分配
C的初始动态分配语句为:
L.data=(ElemType*)malloc(sizeof(ElemType)\*InitSize);
说明:
-
malloc函数返回一个指针类型,需要强制转换为你定义的数据元素类型指针。
-
malloc函数的参数,InitSize表示要分配多大的连续内存空间。
-
对于malloc函数申请的空间,如果要释放需要使用free函数。
5、基本操作
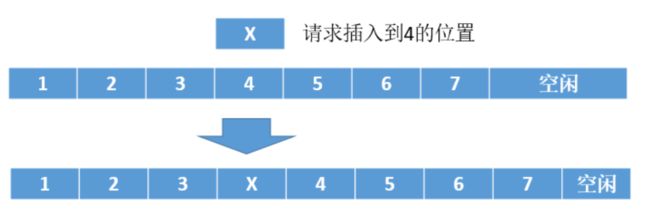
(1)插入操作
插入操作需要将要插入位置之后的所有元素向后移动1位。
时间复杂度分析:
最好情况:在表尾插入元素,不需要移动元素,时间复杂度为O(1)。
最坏情况:在表头插入元素,所有元素依次后移,时间复杂度为O(n)。
平均情况:在插入位置概率均等的情况下,平均移动元素的次数为n/2,时间复杂度为O(n)。
说明:数组的下标是从0开始的,但是这里说的第几个元素是表示顺序表的位序,是从1开始的。第i个元素,下标实际为i-1。
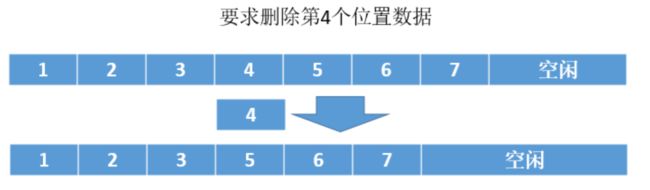
(2)删除操作
删除操作需要将要删除位置之后的所有元素向前移动1位。
时间复杂度分析:
最好情况:删除表尾元素,不需要移动任何元素,时间复杂度为O(1)。
最坏情况:删除表头元素,之后的所有元素依次前移,时间复杂度为O(n)。
平均情况:在删除位置概率均等的情况下,平均移动元素的次数为(n-1)/2,时间复杂度为O(n)。
说明:数组的下标是从0开始的,但是这里说的第几个元素是表示顺序表的位序,是从1开始的。第i个元素,下标实际为i-1。
(3)按值查找
时间复杂度分析:
最好情况:查找元素在第一个位置,时间复杂度为O(1)。
最坏情况:查找元素在最后一个位置,时间复杂度为O(n)。
平均情况:在查找位置概率均等的情况下,平均查找次数为(n-1)/2,时间复杂度为O(n)。
(4)按位查找
时间复杂度分析:
按位查找时,由于顺序表的各个数据元素在内存中连续存放,具有“随机存取”特性。因此时间复杂度为O(1)。