数据结构——栈和队列

数据结构课程学习记录。

一、栈的基本概念

栈（Stack）只允许在一段端进行插入或删除操作的线性表。可以进行出栈入栈的操作一端称为栈顶(yop)，无法进行出栈入栈操作的一端称为栈底(bottom)
栈的基本操作：

InitStack(&S):初始一个空栈S。
StackEmpty(S):判断一个栈是否为空，若栈为空则返回true,否则返回false。
Puch(&S,x):进栈，若栈S未满，则将x加入使之成为新栈顶。
Pop(&s,&x):出栈，若栈元素非空，则弹出栈顶元素，并用x返回。
GetTop(S,&x):读栈顶元素，若栈空则用x返回栈顶元素。
ClearStack(&S):销毁栈，并释放S占用的内存空间。

二、栈的两种数据结构

栈的顺序结构

顺序栈：采用顺序存储的栈

#define MaxSize 50
typedef struct{
    ElemType data[MaxSize];
    int top;  
}SqStack;

我们从结构体中可以看出，只有指向栈顶元素的指针top，没有标注长度的length，那么如何求算顺序栈数据元素的数量？如何判定空栈？如何判断栈满？

顺序栈
栈空条件:S.top == -1
栈长    :S.top + 1//数组下标是从0开始的，顺序栈的元素下标是从1开始的
栈满条件:S.top == MaxSize - 1

初始化空栈操作

void InitStack(SqStack &S){
    S.top == -1;
}

判断栈空

bool StackEmpty(SqStack S){
    if(S.top == -1)
      return true;
    else
      return false;
}

进栈

bool Puch(SquStack &S, ElemType x){
    if(S.top == MaxSize - 1)  //判断数组是否满了
        return false;
    S.data[++S.top] = x;
    return true;
}

出栈

bool Pop(SqStack &S, ElemType &x){
    if(S.top == -1)
        return false;
    x = S.data[S.top --];
    return true;
}

读出栈顶元素

bool GetTop(SqStack S, ElemType &x){
    if(S.top == -1)
        return false;
    x = S.data[S.top];
    return true;
}

共享栈 将两个栈底设置在共享栈的两端，栈顶向空间中间延申
0号栈为上面的栈，1号栈为下面的栈
[0, 1, 2, …, i-1 , i, …, MaxSize-2, MaxSize-1]

共享栈
判空：0号栈top == -1;    1号栈 == MaxSize

栈的链式存储

链栈 采用链式存储的栈

typedef struct Linknode{
    ElemType data;   //保存数据的数据域
    struct Linknode *next;//指向下一个节点的指针域
} *LiStcak;

三、队列的基本概念

队列(Queue): 只允许在表的一端进行插入，表的另一端进行删除操作的线性表（先进先出）
队列的基本操作

InitQueue(&Q):初始化队列，构造一个空队列Q
QueueEmpty(Q):判队列空，若队列Q为空返回true,否则返回false。
EnQueue(&Q, x):入队，若队列Q未满，则将x加入使之成为新的队尾。
DeQueue(&Q, &x):出队，若队列Q非空，则删除队头元素，并用x返回。
GetHead(Q, &x):读队头元素，若队列Q非空则用x返回队头元素。
ClearQueue(&Q):销毁队列，并返回队列Q占用的内存空间。

四、队列的顺序存储和链式存储

队列的顺序存储

顺序队 采用顺序存储的队列

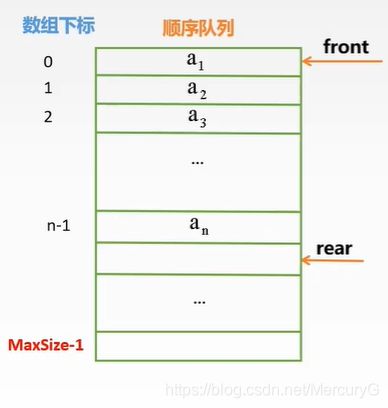
出队操作需要将队首$a_1$元素移出，并将front指针指向下一个元素；
入队操作需要将元素$a_{i+1}$插入到队列当中，并移动rear指针指向下一个位置

#define MaxSize 50
typedef struct{
    ElemType data[MaxSize];
    int front, rear;
}SqQueue;

判空条件：   Q.front == Q.rear
求队列长度： Q.rear - Q.front
队满条件：   Q.rear == MaxSize(此判断方法会产生家溢出问题)

循环队列 把存储队列的顺序队列在逻辑上视为一个环

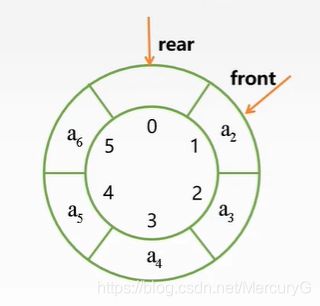
如何将指向Maxsize的rear指针改为循环的指向位置呢？
使用**取余（%MaxSize）**操作

front指针移动：Q.front = (Q.front + 1)  %  MaxSize
rear指针移动： Q.rear = (Q.rear + 1)  % MaxSize
队列长度：    (Q.rear + MaxSize - Q.front)  %  MaxSize

循环队列
队空条件： Q.front == Q.rear
队满条件： Q.feont == Q.rear
明显此处出现了冲突，判断条件并无法使用

解决循环队列判空判满条件冲突的方法：
方法一：牺牲一个存储单元

对空条件： Q.front == Q.rear
队满条件： Q.front ==(Q.rear + 1) % MaxSize  (判断rear是否在front之前)

方法二：增加一个变量代表元素的个数

Q.size：队列内元素个数
队空条件：Q.size == 0
队满条件：Q.size == MaxSize(数组容量的最大值)

方法三：增加tag标识
增加tag表示来标识插入和删除操作；
我们发现，对空是由删除操作引起的，当队列当中只剩下一个元素时，进行删除（出队）操作，就会引起队空，队满是由于入队（插入）操作引起的。

队空条件：Q.front == Q.rear && tag == 0
队满条件：Q.front == Q.rear && tag == 1

循环队列的基本操作

初始化操作：

void InitQueue(SqQueue &Q){
    Q.rear == Q.front = 0;
}

判断队空操作：

bool isEmpty(SqQueue Q){
    if(Q.rear == Q.front)
        return turn;
    else
        return false;
}

入队操作：

bool EnQueue(SqQueue &Q, ElemType x){
    //Q为入队的队列，x为入队的元素
    if((Q.rear + 1) % MaxSize == Q.front) //首先判断队列是否已满
        return false;
    Q.data[Q.rear] == x;
    Q.rear == (Q.rear + 1) % MaxSize;
    return true;
}

出队操作：

bool DeQueue(SqQueue &Q, ElemType &x){
    if(Q.rear == Q.front); //首先判断队列是否为空
        return false
    x = Q.data[Q.front];
    Q.front = (Q.front + 1) % MaxSize;
    return true;
}

队列的链式存储

链队 采用链式存储的队列

实现链队的结构体：

//实现链队当中每一个节点的结构体
typedef struct{
    ElemType data;  // 保存数据的data
    struct LinkNode *next; // 指向下一个节点的指针next
}LinkNode;

//链队的结构体
typedef struct{
    LinkNode *front, *rear; 
}LinkQueue;

链队的基本操作

初始化操作：初始化一个空的队列，就是要生成一个头结点，并把两个指针指向该头结点。

void InitQueue(LinkQueue &Q){
    Q.front = (LinkNode*)malloc(sizeof(LinkNode)); //初始化头结点，并把front指向它
    Q.rear = Q.front; // 将rear指针指向front
    Q.front->next = NULL; //将该节点的next域置为空
}

判断队列是否为空的操作：当front指针和rear指针都指向了头结点时为空队列

void isEmpty(LinkQueue Q){
    if(Q.front == Qrear)
        return true;
    else
        return false;
}

入队操作：链队的入队操作就相当于单链表的尾插法。

void EnQueue(LinkQueue &Q, ElemType x){
    //申请一个新的节点空间，s所指向的空间
    LinkNode *s = (LinkNode *)malloc(sizeof(LinkNode)); 
    //保存数据域，将其next域置为空
    s->data = x;
    s->next = NULL;
    //尾插法的具体实现过程
    Q.rear->next = s;
    Q.rear = s;
}

出队操作：链队的出队操作于单链表的头删除非常的相似。

bool DeQueue(LinkQueue &Q, ElemType &x){
    if(Q.front == Qrear) // 判断队列是否为空
         return false;
     //首先创建指针类型的变量p来保存改节点的地址
     LinkNode *p = Q.front->next;
     //将数据元素保存在x当中
     x = p->data;
     //将头节点的next指针指向下一个数据元素节点，也就是p的next指针所指向的节点
     Q.front->next = p->next;
     //如果改链队当中只有一个数据节点，在删除后，rear指针指向头结点，所以此处进行判断
     if(Q.rear == p) //如果rear是第一个数据元素节点
         Q.rear = Q.front;
     free(p);
     return true;
}

五、双端队列

输出序列

连续输入和输出
在栈中，输入和输出序列是逆序
输入序列：1，2，3，…，n
输出序列：n，…，3，2，1
而在队列中，输入和输出序列是一致的

合法出栈序列的个数
进栈序列：1，2，3，…，k，…，n
出栈序列：（1 ~ k-1），（k+1 ~ n）, k
　　比k小的出栈序列 　比Ｋ大的出栈序列

所以合法出栈序列个数的公式为：
$f(n)=f(0)\ast f(n-1)+f(1)\ast f(n-2)+\cdot \cdot \cdot +f(n-2)\ast f(1)+f(n-1)\ast f(0)$且$f(0)=f(1)=1$
我们可以通过数学证明过程得到公式：
$f(n)=C(2n,n)/(n+1)$

双端队列

双端队列 循序两端都可以进行入队及出队操作的序列

用输入序列：1，2，3，4为例：
输出受限的双端队列：只能在一端进行删除，两端都可以进行插入
不合法输出序列的个数：
当我们忽视一端插入，只看同端插入和删除时会发现，此时为栈，于是先减去在栈中合法输出的序列：
$4!-C(8,4)/5=4!-14=10$
再加上原本被我们忽视的那一端插入后，可以通过推导得知有2个不是合法序列
输入受限的双端队列：只能在一端进行插入，两端都可以进行删除
屏蔽一端删除仍为栈，思路于上一个相同

六、栈和队列的应用

括号匹配

①匹配序列：每个左括号有与之匹配的右括号
②不匹配序列
算法思想：
1)出是一个空栈，顺序读入括号
2)若是右括号，则与栈顶元素进行匹配
　· 若匹配，则弹出栈顶元素并进行下一个元素
　· 若不匹配，则该序列不合法
3)若是左括号，则压入栈中
4)若全部元素遍历完毕，栈中非空则序列不合法

表达式求值

[(A + B) * C] -[E - F]
中缀表达式转前缀表达式：
A 　　　+　 　　 B 　　　=> 　　+AB
+AB　　 * 　 　　C 　　　=> 　　*+ABC
+ABC　－　　　-EF　　=>　　　-+ABC-EF
中缀表达式转后缀表达式：
结果为：AB+CEF–
中缀转后缀利用栈来实现的算法思想：
遇到数字时直接加入后缀表达式
遇到运算符时：
a、若为’(’，入栈
b、若为’)’，则依次把栈中的运算符加入后缀表达式，直到出现’(’，并从栈中删除’(’；
c、若为’ + ‘，’ - ‘，’ * ‘，’ / ‘，
　　栈空，入栈；
　　栈顶元素为’(’，入栈；
　　高于栈顶元素优先级，入栈；
　　否则，依次弹出栈顶运算符，直到一个优先级比它低的预算夫或’('为止；
d、遍历完成，若栈非空则依次弹出所有元素

递归

递归若在一个函数，过程或数据结构的定义中有应用了它自身，则称他为递归定义的，简称递归
实现斐波那契数列：
$$fib(n)=\{\begin{array}{ll}fib(n-1)+fib(n-2),& \text{n>1}\\ 1,& \text{n=1}\\ 0,& \text{n=0}\end{array}$$

int Fib(int n){
    if(n == 0)
        return 0;
    else if(n == 1)
        return 1;
    else
        return Fib(n-1) + Fib(n-2)
}

递归产生的问题：
　　在递归调用过程中，系统为每一层的返回点、局部变量、传入实参等开辟了递归工作栈来进行数据存储，递归次数多了容易造成栈溢出。
　　通常情况下，递归的效率并不高。

七、数组的定义和存储结构

数组是由n(n>=1)个相同类型的元素构成的有限序列，每个数据元素称为一个数组元素，每个元素受n个线性关系的约束，每个元素在n个线性关系中的序号称为该元素的下标，并称该数组为n维数组。
数组的维度和维界是不可变的
　　数组一旦被定义，其维度和维界不可变，数组花除初始化和销毁外，只有存取元素和修改元素的操作。

存储结构

采用顺序存储的方法
对于按行优先存储的二维数组，我们想要计算第i行，第j列这个元素的地址：
　　·首先有第一个元素的地址，
　　·按行优先要把之前的每一行都遍历完才可以存储该数组元素，所以需要将之前所有的行所用到的存储空间计算出来，在$a_{i,j}$之前一共有$i$行，$i$乘以每一行数组元素的个数从0到n一共$n+1$个，然后乘以L，L为每个数组元素所使用的空间大小
　　·$a_{i,j}$个数组元素在第$i$行之前还有一些数组元素，他们也会比$a_{i,j}$先进入存储空间，需要加上这些元素所使用的存储空间

按列优先存储：

八、矩阵的压缩存储

**对称矩阵：**若对一个n阶方阵A[1…n][1…n]中的任意元素$a_{i,j}$都有$a_{i,j}=a_{j,i}(1\le i,j\le n)$，则称其为对称矩阵。
如何计算矩阵中元素的数组下标k：

三角矩阵 若对一个n阶方阵A[1…n][1…n]中上（下）三角矩阵均为同一常量，则称为下（上）三角矩阵。
如何压缩存放此种矩阵？
存放数组$B[n(n+1)/2+1]$
注： 此处末尾的’ +1 '表示的是会把常数c存放在该数组B的最后一个单元上


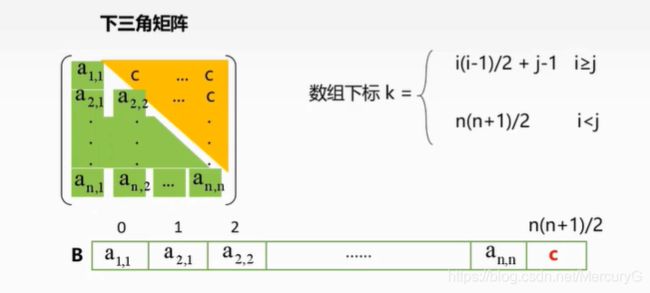
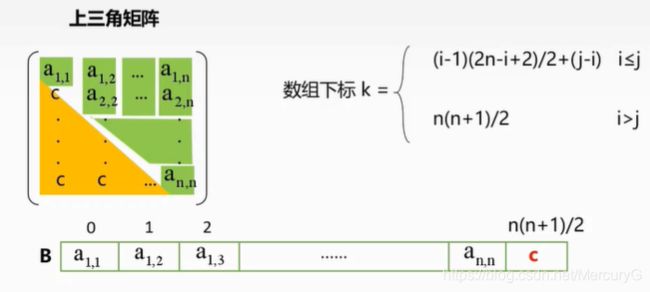
三对角矩阵： 若对一个n阶方阵A中的任意元素$a_{i,j}$，当$|i-j|>1$有$a_{i,j}=0(1\le i,j\le n)$，则称为三角对称矩阵。

稀疏矩阵： 矩阵元素的个数s相对于矩阵中非零元素的个数t来说非常多，即s >> t的矩阵称为叙述矩阵。