数据结构--克鲁斯卡尔(kruskal)算法（大话数据结构）

什么是克鲁斯卡尔(kruskal)算法

这里我们选用普里姆（prim）算法作为对比，prim算法是从一个顶点开始搜索最小路径，而克鲁斯卡尔算法是通过一个遍历好的边集数组搜索出一条最短路径。（最短路径的本质就是最小生成树。）

克鲁斯卡尔算法与普里姆算法的区别在哪里呢

克鲁斯卡尔是从边集表出发，遍历图从而生成最小树。对于边数比较少的图来说相较于普里姆算法更游刃有余。即克鲁斯卡尔算法更适宜于稀疏图，普里姆算法适宜于稠密图。

##克鲁斯卡尔算法理论

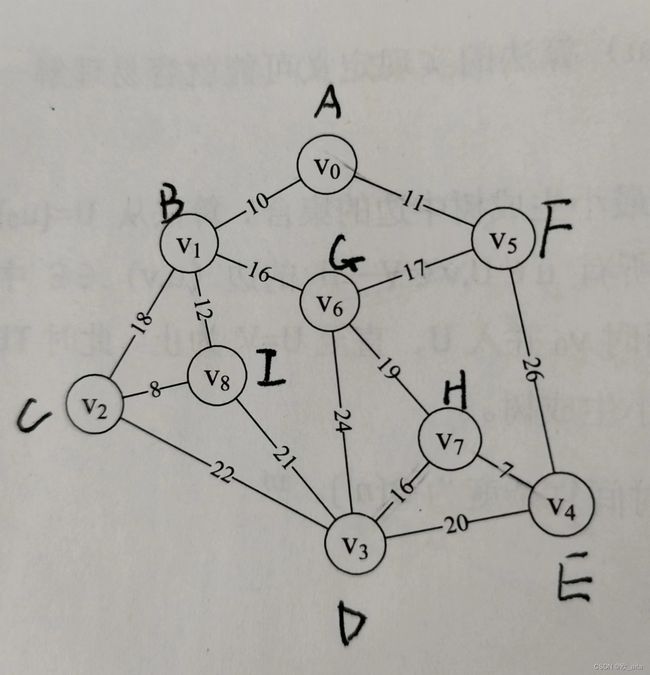
如图1所示，这是一个有9个顶点15条边的图。
首先，先遍历所有边，将权值从小到大排序入数组。如图2所示，

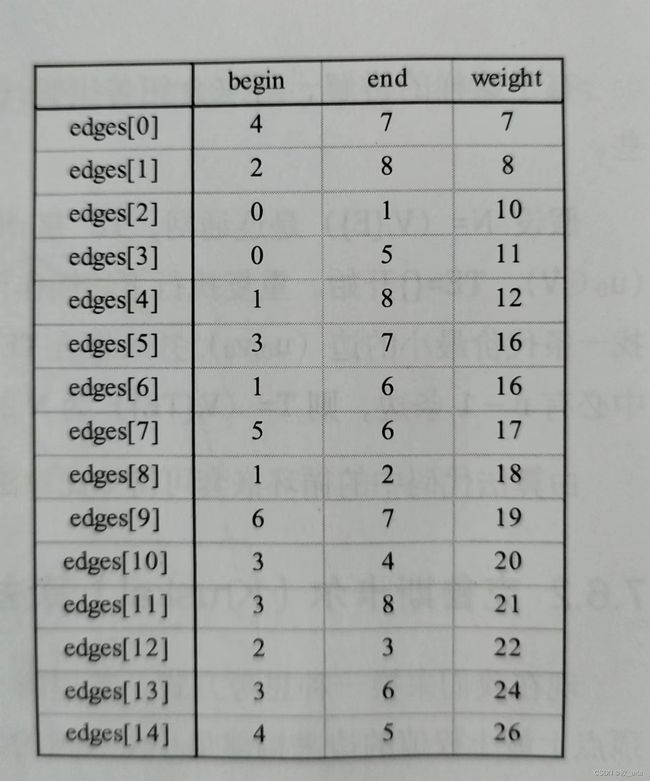
再这个基础上，搜索出遍历所有顶点的最短路径。（并且是所有顶点联通的路径）（如图3所示）

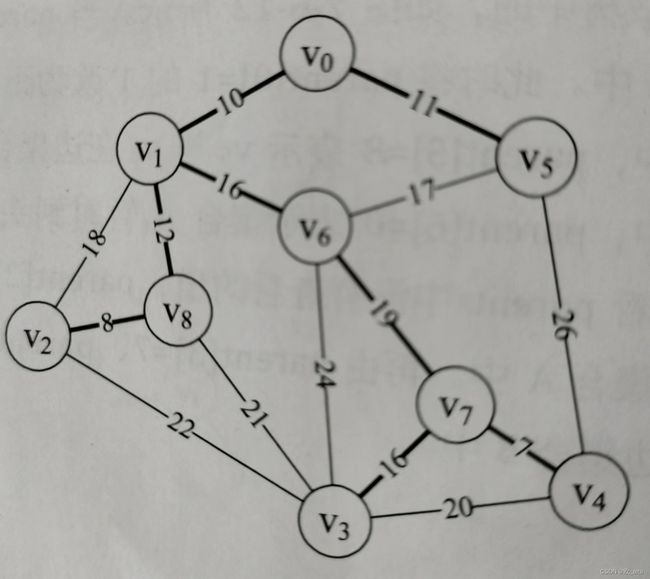
以上就是大概的思路了。

克鲁斯卡尔算法实现

宏定义

#include 
#include 
#define MAXVEX 100
#define INFINITY 65535 //65535代表无穷大

对边集数组进行定义

typedef struct {
	int begin;    //记录边的起始顶点
	int end;      //记录边的终点
	int weight;   //记录边的权值
}Edge;

创建邻接矩阵的代码由于太占篇幅，所以省略了，不过有兴趣的可以查看
邻接矩阵

克鲁斯卡尔算法

void MiniSpanTree_Kruskal(MGraph G)
{
	int i, m;
	int parent[MAXVEX];
	int j, w, t;
	int n = 0;
	int k = 0;
	Edge edges[MAXVEX];

	while (k<G.numEdges)        //建立边集数组
	{
		int min = INFINITY;
		for (i = 0; i < G.numVertexes; i++)
		{
			for (j = 0; j < G.numVertexes; j++)
			{
				if (G.arc[i][j] < min && G.arc[i][j]>0)
				{
					min = G.arc[i][j];

					w = i;
					t = j;
				}
			}
			
		}
		G.arc[w][t] = 0;
		G.arc[t][w] = 0;
		edges[k].begin = w;
		edges[k].end = t;
		edges[k].weight = min;
		k++;
	}

	for (i = 0; i < G.numVertexes; i++)
		parent[i] = 0;

	for (i = 0; i < G.numEdges; i++)            //循环每一条边
	{
		n = Find(parent, edges[i].begin);
		m = Find(parent, edges[i].end);
		
		if (n != m)                          //防止生成环路
		{
			parent[n] = m;

			printf("(%d, %d) %d", edges[i].begin,   //入最小生生成
				edges[i].end, edges[i].weight);     //树，打印顶点
		}                                           //和权值
	}      

    //以下可以作为测试数组和parent数组是否正确
	printf("\n");
	for (i = 0; i < G.numVertexes; i++)
		printf("%d ", parent[i]);

	printf("\n");
	for (i = 0; i < G.numEdges; i++)
	{
		printf("\n%d ", edges[i].begin);
		printf("%d ", edges[i].end);
		printf("%d ", edges[i].weight);
	}
}

Find函数定义

int Find(int* parent, int f)    //查找连线顶点的下标
{
	while (parent[f] > 0)
		f = parent[f];
	return f;
}

主函数

int main()
{
	MGraph G;
	CreateMGraph(&G);
	MiniSpanTree_Kruskal(G);
	return 0;
}

测试

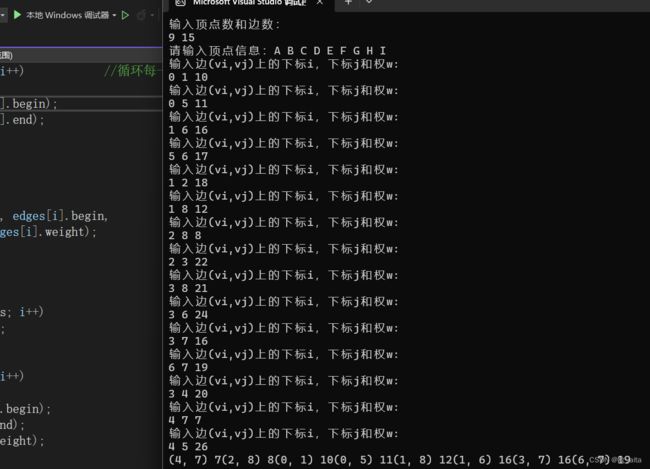
在控制台最下一行就是最小生成树的结果（V4,V7）7…

parent[]={1,5,8,7,7,8,7,0,6}

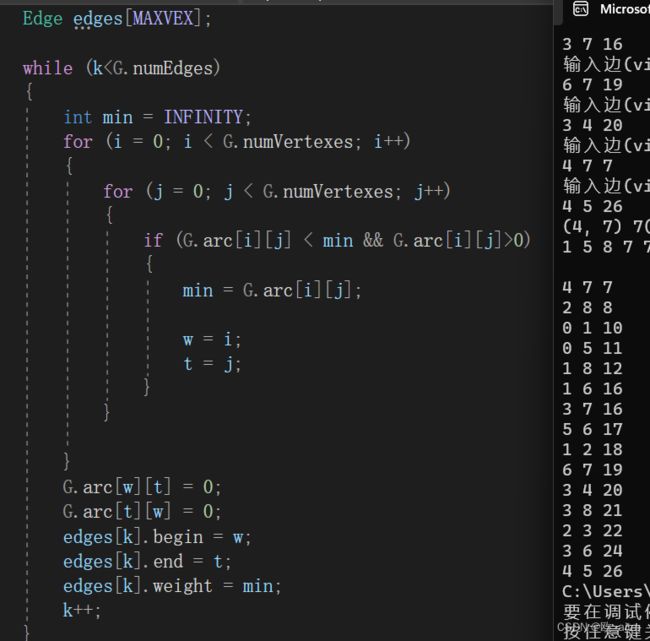
最下边一大长串就是对应的边集数组。

代码解读

1. 克鲁斯卡尔算法的准备工作，定义变量。
   使用parent[]是为了辨别顶点并且进行入最小生成树操作，使用edges[]来对数组权值进行排序。

int i, m，j, w, t;
int parent[MAXVEX];
int n = 0;
int k = 0;
Edge edges[MAXVEX]; 

2.边集树组排序，这里使用的是三重枚举方法（主要是没想到好的算法）。

while (k<G.numEdges)
{
	int min = INFINITY;
	for (i = 0; i < G.numVertexes; i++)
	{
		for (j = 0; j < G.numVertexes; j++)
		{
			if (G.arc[i][j] < min && G.arc[i][j]>0)
			{
				min = G.arc[i][j];

				w = i;
				t = j;
			}
		}
		
	}
	G.arc[w][t] = 0;
	G.arc[t][w] = 0;
	edges[k].begin = w;
	edges[k].end = t;
	edges[k].weight = min;
	k++;
}

在之前的整体代码测试中也展现过，这个数组的大概摸样。这里再放一次。

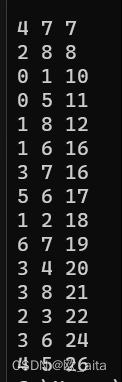
3.对parent[]进行初始化操作（具体操做之后说）

for (i = 0; i < G.numVertexes; i++)
	parent[i] = 0;

4.开始按照边集数组顺序遍历每一条边

同时要避免造成环路，形成了两条不相连的连通分量

for (i = 0; i < G.numEdges; i++)            //循环每一条边
{
	n = Find(parent, edges[i].begin);
	m = Find(parent, edges[i].end);
	
	if (n != m)               //如果n==m,就说明形成了闭环，造成了有两条不相连的联通分量
	{
		parent[n] = m;

		printf("(%d, %d) %d", edges[i].begin,//打印操作
			edges[i].end, edges[i].weight);
	}
}

5.fund函数定义

一个萝卜一个坑，如果在parent[]中有该顶点的下标，就说明该点已经进入最小生成树。

int Find(int* parent, int f)    //查找连线顶点的下标
{
	while (parent[f] > 0)
		f = parent[f];
	return f;
}