数据结构 - 第 3 章 栈和队列

【考纲内容】

(1). 栈和队列的基本概念

(2). 栈和队列的顺序存储结构

(3). 栈和队列的链式存储结构

(4). 栈和队列的应用

【知识框架】

【复习提示】

(1). 本章通常以选择题的形式考查，题目不算难，但命题的形式比较灵活

(2). 其中，栈（出入栈的过程 、出栈序列的合法性）和队列的操作及其特征是考查重点

(3). 栈和队列都是线性表的应用和推广，因此也容易出现在算法设计题中

(4). 此外，栈和队列的顺序存储 、链式存储及其特点 、双端队列的特点 、栈和队列的常见应用，以及数组和特殊矩阵的压缩存储都是必须要掌握的内容

3.1 栈

3.1.1 栈的基本概念

1. 栈的定义
栈的概念	栈（Stack）是只允许在一端进行插入或删除操作的线性表 (i). 栈是一种线性表 (ii). 限定只能在线性表的一端进行插入和删除    （插入和删除在线性表的同一端）
栈顶	线性表中允许进行插入和删除操作的一端（瓶口）
栈底	固定的，线性表中不允许插入和删除操作的一端（瓶底）
空栈	不包含任何元素的空的线性表
栈的表示	假设某个栈  ，如下图所示，则  为栈底元素，  为栈顶元素
栈的特性	由于栈只能在栈顶进行插入和删除操作，进栈次序依次为  ， 而出栈次序为  由此可见，栈的操作特性可以明显地概括为后进先出（Last In First Out ，LIFO）
栈的数学性质	个不同元素进栈，出栈元素不同排列的个数为  上述公式称为卡特兰（Catalan）数，可采用数学归纳法证明
###############################################################################
2. 栈的基本操作
Init(&S)	初始化一个空栈 S
Empty(S)	判断一个栈是否为空，为空返回 true ，不为空返回 false
Push(&S,x)	进栈，若栈 S 未满，则将元素 x 插入，并使元素 x 成为新的栈顶
Pop(&S, &x)	出栈，若栈 S 非空，则弹出栈顶元素，并用元素 x 返回
GetTop(S, &x)	获取栈顶元素，若栈 S 非空，则用元素 x 返回栈顶元素
Destory(&S)	销毁栈，释放栈 S 占用的存储空间

3.1.2 栈的顺序存储结构

    栈是一种操作受限的线性表，类似于线性表，栈也有两种存储方式

1. 顺序栈的实现

概念	采用顺序存储的栈，称为顺序栈
顺序栈的实现	(i).  利用一组地址连续的存储单元，存放从栈底到栈顶的数据元素 (ii). 附设一个指针（top）指向当前栈顶元素的位置 所谓指针，其实是一个整数，保存栈顶元素的下标
栈的顺序存储 类型描述	#define  MaxSize  50                       // 定义栈中元素的最大个数 typedef  struct  {         ElemType  data[MaxSize]；    // 存放栈中元素         int  top；                                   // 栈顶指针 } SqStack；
栈顶指针	S->top ，初始状态设置为 S->top = -1
栈顶元素	S->data[S->top]
进栈操作	栈不满时，先将栈顶指针 top 加 1 ，再将值插入新的栈顶位置； S->top++； S->data[S->top] = x；
出栈操作	栈非空时，先获取栈顶元素，再将栈顶指针减 1 ； x = S->data[S->top]； S->top--；
栈空条件	判断 S->top == -1
栈满条件	判断 S->top == MaxSize - 1
栈长 （实际元素个数）	S->top + 1
说明	由于顺序栈的入栈操作受数组上限的约束，当对栈的最大使用空间估计不足时， 有可能发生栈上溢，此时应及时向用户报告消息，以便及时处理，避免出错
注意	栈和队列的判空 、判满条件，会因具体实现而不同，上面提到的方法以及下面的代码 实现只是在栈顶指针设定的条件下的相应方法 top == -1 为栈空条件，这是接口代码实现的前提

2. 顺序栈的基本运算

下面是顺序栈上常用的基本运算的实现

注意：假如存储空间是在栈空间或静态空间上分配的，则无需手动销毁

2.1  顺序栈的 C 描述

#define INIT_SIZE 50
#define INCREASEMENT_SIZE 10

#define OK 1
#define ERROR -1

#define YES 1
#define NO 0

typedef int Status;
typedef int ElemType;

typedef struct {
    ElemType *data;
    int top;
} SeqStack;

/*
 * 初始化
 */
Status Init(SeqStack *S)
{
    S->data = (ElemType*)malloc(sizeof(ElemType) * INIT_SIZE);
    if (S->data == NULL)
    {
        printf("Out of memory !\n");
        return ERROR;
    }

    S->top = -1;
    return OK;
}

/*
 * 判栈空
 */
Status Empty(SeqStack *S)
{
    if (S->top == -1)
        return YES;
    else
        return NO;
}

/*
 * 进栈
 */
Status Push(SeqStack *S, ElemType x)
{
    if (S->top == INIT_SIZE - 1)
        return ERROR;

    S->top++;
    S->data[S->top] = x;
    return OK;
}

/*
 * 出栈
 */
Status Pop(SeqStack *S, ElemType *x)
{
    if (S->top == -1)
        return ERROR;

    *x = S->data[S->top];
    S->top--;
    return OK:
}

/*
 * 获取栈顶元素 
 */
Status GetTop(SeqStack *S, ElemType *x)
{
    if (S->top == -1)
        return ERROR;

    *x = S->data[S->top];
    return OK;
}

/*
 * 销毁栈 
 */
Status Destroy(SeqStack *S)
{
    free(S->data);
    S->data = NULL;
    return OK;
}

2.2 顺序栈的 C++ 描述

#include 
#include 
#include 
#include 

using namespace std;

#define MaxSize 50

using ElemType = int;

class Stack
{
public:
    Stack() = default;
    Stack(int initsize);
    ~Stack();
    bool empty();
    void push(ElemType x);
    void pop();
    ElemType getop();
private:
    ElemType *elem;
    int top;
};


int main(int argc, char* argv[])
{
    Stack stack{10};
    stack.push(2);
    stack.push(3);
    stack.push(7);
    stack.push(11);
    stack.push(13);

    std::cout << stack.getop() << std::endl;
    stack.pop();
    std::cout << stack.getop() << std::endl;
    stack.pop();
    std::cout << stack.getop() << std::endl;
    stack.pop();
    return 0;
}


/* 构造函数 */
Stack::Stack(int initsize)
: top(-1)
{
    elem = new ElemType[initsize];
    std::cout << "Construct" << std::endl;
}

/* 析构函数 */
Stack::~Stack()
{
    delete[] elem;
    std::cout << "Destroy" << std::endl;
}

/* 判栈空 */
bool Stack::empty()
{
    return top == -1;
}

/* 进栈 */
void Stack::push(ElemType x)
{
    if (top == MaxSize - 1)
    {
        std::cout << "Stack is full !\n" << std::endl;
        return;
    }

    std::cout << "push element is " << x << std::endl;
    ++top;
    elem[top] = x;
}

/* 出栈 */
void Stack::pop()
{
    if (top == -1)
    {
        std::cout << "Stack is empty !\n" << std::endl;
        return;
    }
    
    std::cout << "pop element is " << elem[top] << std::endl;
    top--;
}

/* 获取栈顶元素 */
ElemType Stack::getop()
{
    if (top == -1)
    {
        std::cout << "Stack is empty !\n" << std::endl;
        return ElemType{};
    }

    return elem[top];
}

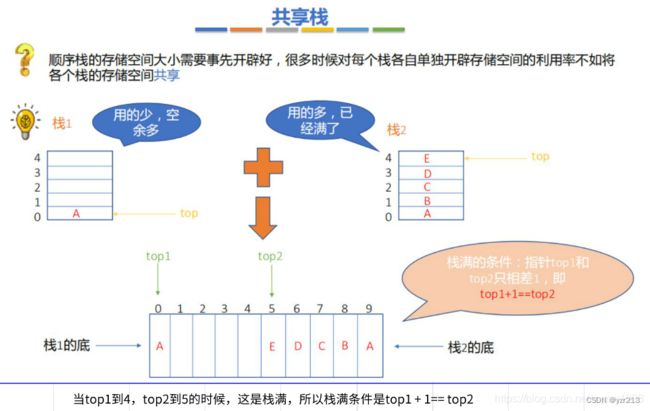
3. 共享栈

共享栈
共享栈概念	利用栈底位置相对不变的特性，可以让两个顺序栈共享一个一维数组空间； 将两个栈的栈底分别设置在共享空间的两端，两个栈顶向共享空间的中间延伸
栈空	两个栈的栈顶指针都指向栈顶元素； top1 = -1 时，1 号栈为空； top2 = MaxSize 时，2 号栈为空；
栈满	仅当两个栈顶指针相邻（top1 + 1 = top2 ）时，判断为栈满
进栈	当 1 号栈进栈时， top1 先加 1 再插入新元素 s1->top1++; s1->data[s1->top1] = x; 当 2 号栈进栈时，top2 先减 1 再插入新元素 s2->top2--; s2->data[s2->top2] = x;
出栈	当 1 号栈出栈时，先返回 1 号栈的栈顶元素，再将 1 号栈顶指针减 1 x = s1->data[s1->top1]; s1->top1--; 当 2 号栈出栈时，先返回 2 号栈的栈顶元素，再将 2 号栈顶指针加 1 x = s2->data[s2->top2]; s2->top2++;
总结	共享栈是为了更有效地利用存储空间，两个栈的空间相互调节，只有在整个存储空间被占满时才发生上溢； 存取数据的时间复杂度均为  ，所以对存取效率没什么影响

3.1.3 栈的链式存储结构

概念	采用链式存储的栈称为 "链栈"
链栈的优点	便于多个栈共享存储空间和提高其效率，不存在栈满上溢的情况
链栈的实现	通常采用单链表实现； 规定栈顶在单链表的表头（即，插入删除元素均在表头）
此处规定	链栈没有头结点，链表的头指针指向栈顶元素
栈的链式 存储类型	typedef  struct  Linknode {         ElemType  data;            // 数据域         struct Linknode *next;    // 指针域 } *LiStack;                              // 栈类型定义
总结	采用链式存储，便于结点的插入与删除； 链栈的操作与链表类似，入栈和出栈的操作都在链表的表头进行；

(1). 链式栈的描述

#include 
#include 

typedef int ElemType;

struct Node;
typedef struct Node *PtrToNode;
typedef PtrToNode List;
typedef PtrToNode Position;

struct Node
{
    ElemType Elem;
    Position Next;
};


List InitStack(List L);
int Empty(List L);
void PrintEmpty(List L);
void Push(List L, ElemType E);
void Pop(List L);
ElemType Top(List L);
void PrintTop(List L);
void DestroyStack(List L);



int main(int argc, char* argv[])
{
    List L = NULL;
    L = InitStack(L);
    PrintEmpty(L);

    Push(L, 2);
    Push(L, 3);
    Push(L, 5);
    Push(L, 7);
    Push(L, 11);
    Push(L, 13);

    PrintEmpty(L);
/*
    PrintTop(L);
    Pop(L);
    PrintTop(L);
    Pop(L);
    PrintTop(L);
    Pop(L);
    PrintTop(L);
    Pop(L);
    PrintTop(L);
    Pop(L);
*/


    DestroyStack(L);
    PrintEmpty(L);

    return 0;
}


List InitStack(List L)
{
    L = (List)malloc(sizeof(struct Node));
    if (!L)
        return NULL;

    L->Next = NULL;
    return L;
}

int Empty(List L)
{
    return L->Next == NULL;
}

void PrintEmpty(List L)
{
    if (Empty(L) != 0)
        printf("Empty\n");
    else
        printf("Not Empty\n");
}

void Push(List L, ElemType E)
{
    Position NewCell;

    NewCell = (Position)malloc(sizeof(struct Node));
    if (NewCell == NULL)
    {
        printf("Out of memory!\n");
        exit(0);
    }

    NewCell->Elem = E;
    NewCell->Next = L->Next;
    L->Next = NewCell;
}


void Pop(List L)
{
    Position TmpCell = NULL;

    if (L->Next == NULL)
    {
        printf("Empty Stack!\n");
        return;
    }

    TmpCell = L->Next;
    L->Next = TmpCell->Next;
    free(TmpCell);
    return;
}

ElemType Top(List L)
{
    ElemType data;

    if (L->Next == NULL)
    {
        printf("Empty Stack!\n");
        return data;
    }

    data = L->Next->Elem;
    return data;
}

void PrintTop(List L)
{
    ElemType Elem = Top(L);

    printf("Top Elem is %d\n", Elem);
}

void DestroyStack(List L)
{
    Position P, TmpCell;

    P = L->Next;
    L->Next = NULL;

    while (P != NULL)
    {
        TmpCell = P->Next;
        printf("Current destroyed element is %d\n", P->Elem);
        free(P);
        P = TmpCell;
    }
}

3.2 栈的应用举例

3.2.1 数制转换

3.2.2 括号匹配的检验

	初始设置一个空栈

bool isValid(string s) 
{
    if (s.size() % 2 == 1)
    {
        return false;
    }

    std::stack chStack;

    for (auto ch : s)
    {
        switch (ch)
        {
            case '(':
            case '[':
            case '{':
                chStack.push(ch);
                break;
            case ')':
                if (chStack.empty() == true || chStack.top() != '(')
                    return false;
                else
                    chStack.pop();
                break;
            case ']':
                if (chStack.empty() == true || chStack.top() != '[')
                    return false;
                else
                    chStack.pop();
                break;
            case '}':
                if (chStack.empty() == true || chStack.top() != '{')
                    return false;
                else
                    chStack.pop();
                break;
            default:
                return false;
        }
    }
    return chStack.empty();
}

3.2.3 行编辑程序

3.2.4 迷宫求解

3.2.5 表达式求值

3.3 栈与递归的实现

3.4 队列

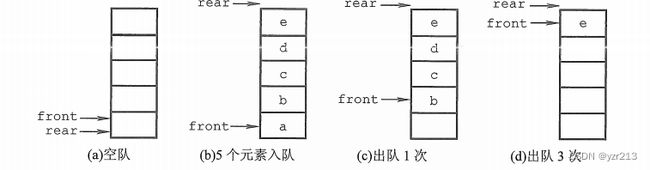
3.4.1 队列的基本概念

队列的基本概念
队列的定义	队列（Queue）简称 "队" ，也是一种操作受限的线性表
	只允许在线性表的一端进行插入，在线性表的另一端进行删除
入队	向线性表的可以插入元素的一端，插入元素，称为 " 入队或进队 "
出队	从线性表的可以删除元素的一端，删除元素，称为 " 出队或离队 "
队列特性	最早入队的元素，也是最早出队 特点就是 " 先进先出 "（First In First Out，FIFO）
队头（Front）	允许删除元素的一端，又称队首
队尾（Rear）	允许插入元素的一端
空队列	不含任何元素的空线性表
队列常见的基本操作
InitQueue(&Q)	初始化队列，构造一个空队列
QueueEmpty(Q)	判别队列是否为空，队列为空返回 true ，队列不为空返回 false
EnQueue(&Q, x)	入队，若队列 Q 未满，将元素 x 插入队尾，并使 x 成为新的队尾元素
DeQueue(&Q, &x)	出队，若队列 Q 非空，删除对头元素，并用元素 x 返回
GetHead(Q, &x)	读取对头元素，若队列 Q 非空，则将对头元素赋值给元素 x
注意	栈和队列都是操作受限的线性表； 因此，不是任何对线性表的操作都可以作为栈和队列的操作； 比如，不可以随便读取栈或队列中间的某个元素

3.4.2 队列的顺序存储结构

1. 队列的顺序存储
基本概念	队列的顺序存储，是指分配一块地址连续的存储单元来存储队列中的元素； 附设两个指针：队头指针 front 指向队头元素，队尾指针 rear 指向队尾元素
队列的顺序 存储类型描述	#define  MaxSize  50                         // 定义队列中元素的最大个数 typedef  struct  {         ElemType  data[MaxSize];        // 存放队列元素         int  front;                                    // 队头指针         int  rear;                                     // 队尾指针 } SqQueue;
队列判空 （初始状态）	Q.front  ==  Q.rear  == 0
进队操作	队列不满时，先将新元素插入队尾位置，再将队尾指针加 1
出队操作	队列不空时，先获取队头元素，再将队头指针加 1
顺序队列 存在的问题	图示 (a) 为队列的初始状态，满足 Q.front == Q.rear == 0 ，该条件可以作为队列判空的条件； 但能否用 Q.rear == MaxSize 作为队列满的条件呢？？？显然不能，图 (d) 中，队列中仅有一个元素，却满足 Q.rear == MaxSize ，这时入队出现 "上溢出" ，但这种溢出并不是真正的溢出，data 数组中依然可以存在可以存放元组的空位置，所以是一种 "假溢出"
队列操作图示
2. 循环队列
解决办法 （循环队列）	前面提到顺序队列的缺点（假溢出），这里引出循环队列的概念
	将顺序队列臆造（假想）为一个环状的空间，即把存储队列元素的表，从逻辑上视为一个 "环" ，称为 "循环队列" 当队首指针 Q.front == MaxSize - 1 后，再前进一个位置就自动到 0 ，这可以利用除法取余运算（%）来实现 再强调一下，队尾插入，队头删除
初始状态 ：	Q.front == Q.rear == 0
队头指针进 1 ：	Q.front = (Q.front + 1) % MaxSize
队尾指针进 1：	Q.rear = (Q.rear + 1) % MaxSize
队列长度：	(Q.rear + MaxSize - Q.front) % MaxSize
入队出队时：	指针都按顺时针方向进 1
循环队列队空和对满的判断条件是什么呢？？？
陷阱	若入队元素的速度快于出队元素的速度，则队尾指针很快就会赶上队头指针； 如图 (d1) 所示，可见队满时也有 Q.front == Q.rear
为了区分队空还是队满，有三种处理方式：
方式一	牺牲一个单元来区分队空和队满； 入队时少用一个队列单元，这是一种较为普遍的做法； 约定以 "队头指针在队尾指针的下一位置作为队满的标志"
	队满条件	(Q.rear + 1) % MaxSize == Q.front
	队空条件	Q.rear == Q.front
	队列中 元素个数	(Q.rear - Q.front + MaxSize) % MaxSize
方式二	类型中增设表示元素个数的数据成员
	队满条件	Q.size == MaxSize
	队空条件	Q.size == 0
	这两种情况都有 Q.front == Q.rear
方式三	队列中增设 tag 数据成员，以区分是队满还是队空
	队满条件	tag == 0 时，若因删除导致 Q.front == Q.rear ，则为队空
	队空条件	tag == 1 时，若因插入导致 Q.front == Q.rear ，则为队满
3. 循环队列的操作
初始化	void InitQueue(SqQueue &Q) {         Q.rear = Q.front = 0； }
队列判空	bool isEmpty(SqQueue Q) {         return Q.rear == Q.front ? true : false； }
入队	bool EnQueue(SqQueue &Q，ElemType x) {         if ((Q.rear + 1) % MaxSize == Q.front)                 return false；         Q.data[Q.rear] = x；         Q.rear = (Q.rear + 1) % MaxSize；         return true； }
出队	bool DeQueue(SqQueue &Q，ElemType &x) {         if (Q.rear == Q.front)                 return false；         x = Q.data[Q.front]；         Q.front = (Q.front + 1) % MaxSize；         return true； }

3.4.3 队列的链式存储结构

1. 队列的链式存储
	队列的链式表示称为 "链队列" 链队列，实际上是一个同时带有队头指针和队尾指针的单链表
	头指针，指向队头结点（第一个存有数据的结点）
	尾指针，指向队尾结点，即单链表的最后一个结点（）
链式队列 类型描述	typedef  struct {         ElemType  data；         struct LinkNode *next； }LinkNode； typedef  struct {         LinkNode *front，*rear； }LinkQueue；
队列判空	当 Q.front == NULL 且 Q.rear == NULL 时，链式队列为空
出队	出队时，首先判断队列是否为空； 队列为空，直接返回； 队列不为空，则取出队头元素，将其从链表中摘除，并让 Q.front 指向下一个结点 （若该结点为最后一个结点，则置 Q.front = Q.rear = 0）
入队	入队时，建立一个新结点，将新结点插入到链表的尾部； 并让 Q.rear 指向这个新插入的结点 （若原队列为空，则令 Q.front 也指向该新结点，）
Tips	不难看出，不带头结点的链式队列，在操作上往往比较麻烦，因此通常将链式队列设计成一个带头结点的单链表，这样插入和删除操作就统一了
注意	用单链表表示的链式队列，特别适合于数据元素变动比较大（经常插入删除）的情形； 不存在队列满且产生溢出的问题
	另外，假如程序中药使用多个队列，与多个栈的情形一样，最好使用链式队列，这样就不会出现存储分配不合理和 "溢出" 的问题
2. 链式队列的基本操作
初始化	void InitQueue(LinkQueue &Q) {         Q.front = Q.rear = (LinkNode*)malloc(sizeof(LinkNode))；         Q.front->next = NULL； }
队列判空	bool IsEmpty(LinkQueue Q) {         return Q.front == Q.rear ? true : false； }
入队	void EnQueue(LinkQueue &Q，ElemType x) {         LinkNode *s = (LinkNode *)malloc(sizeof(LinkNode))；         s->data = x；         s->next = NULL；         Q.rear = s； }
出队	bool DeQueue(LinkQueue &Q，ElemType &x) {         if (Q.rear == Q.front)                 return false；         LinkNode *p = Q.front->next；         x = p->data；         Q.front->front = p->next；         if (Q.rear == p)                 Q.rear = Q.front；         free(p)；         return true； }

3.4.4 双端队列

双端队列概念	双端队列是指，允许两端都可以进行入队和出队操作的队列
	其元素的逻辑结构仍是线性结构
	将队列的两端分别称为前端和后端，两端都可以入队和出队
小结	在双端队列入队时，前端入队的元素在后端入队的元素的前面（更靠近前端）； 后端入队的元素在前端入队的元素的后面（更靠近后端）； 在双端队列出队时，无论是前端出队还是后端出队，先出的元素排列在后出的元素的前面
	输出受限的双端队列 ： 允许在一端进行插入和删除，另一端只允许插入的双端队列， 称为 "输出受限的双端队列"
	输入受限的双端队列 ： 允许在一端进行插入和删除，另一端只允许删除的双端队列， 称为 "输入受限的双端队列"
若限定双端队列，从某个端点插入的元素只能从该端点删除，则该双端队列就蜕变为两个栈底相邻接的栈

3.5 离散事件模拟