【递归专题】汉诺塔详解

【递归专题】汉诺塔详解

目录

汉诺塔背景

​ 传说背景：汉诺塔（又称河内塔），英文名称为Hanoi Tower，是起源于印度的一种古老智力游戏，据传大梵天创造世界的时候，在一块黄铜板上插了三根宝石针，其中一根宝石针从下到上依次穿了64片从大到小的金片，这就是所谓的汉诺塔，每天都有一个僧侣不论白天黑夜，都按照如下的规则移动金片：每次只能移动一片，并且移动的过程中大的金片一定要在小的金片下面，僧侣们预言当所有的金片从梵天穿好的那根针上移动到另一根针上的时候，世界就会在一声霹雳中毁灭，而梵塔、庙宇、众生也都将同归于尽。

现在我们可以简单来计算总的移动次数

1. 移动一个金片需要移动1次

2. 移动两个金片需要移动3次

3. 移动三个金片需要移动7次

   …

4. 我们发现移动次数按照指数递增，那么移动64个金片的总次数为2⁶⁴ - 1，也就是18,446,744,073,709,551,615

现在我们假设这个僧侣1s移动一次金片，并且不需要睡觉吃饭，每天每时每刻都在移动金片，我们将一年为看做365天，一天24h，1小时3600s，那么该僧侣移动的年数大约为594,942,417,355年

这个数字是相当庞大的，不难想象如果我们想要知道所有全部的移动过程，只能借助具有超强算力的计算机如太湖之光了。下面我们就来分析分析汉诺塔这个经典递归问题的解决思路。

汉诺塔递归实现思路

游戏规则

1. 每次只能移动一个盘子
2. 在移动过程中三根杆上都始终保持大盘在下，小盘在上
3. 操作过程中盘子可以置于A、B、C任一杆上。

Step1：如何实现一个盘子的移动

如果只移动一个盘子，实现方式就非常简单了，事实上只需要将A杆当中的盘子直接移动到C杆中就可以

Step2：如何实现两个盘子的移动

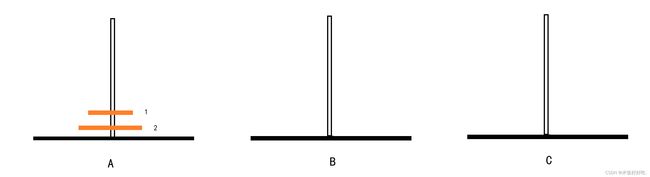
实现两个盘子的思路稍微要比一个盘子的移动复杂，但是我们仍然可以快速找到人工实现的方法。

第一步：我们需要将第一个盘子移到中间位置B。

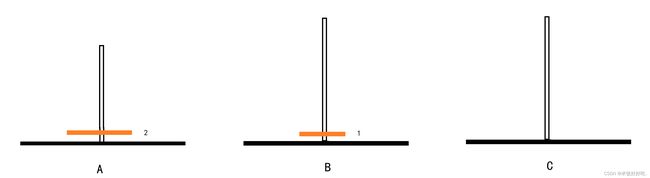
第二步：现在A上只有较大的盘子2，可以直接移到目标位置C杆子上。

第三步：现在临时柱子B中较小盘1可以直接放入目标杆子C上面，且符合规则较小盘在较大盘上面。

第四步：现在也许有人会产生疑惑？难道还需要第四步操作么？不是已经完成需求了吗?是的没错，我们的确已经完成了所有的步骤，但是我们需要抽象出我们解决 这个问题的思路，这是相当关键的。一开始两个盘1、2都位于原杆子A上，现在我们不能直接将两个盘子一起移动，但是如果将第一个盘子直接移动到C，那么就不能符合较小盘位于较大盘之上的规则，这个时候我们内心的想法就是如果可以先将较小的盘子1移到B，然后A中最底层的盘子就可以移动到目标位置了，那么这个问题就等价为如下问题：

1. 如何让较小盘1从A移动到杆子B
2. 让较大盘2移动到目标杆子C
3. 如何让较小盘1从B移动到目标杆子C

Step3：如何实现规模的由大化小

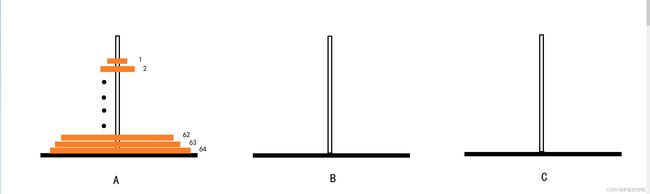
现在我们尝试移动64个盘子，这时我们会感觉头都大了！因为我们这是仅仅靠大脑思考已经难以找到解决办法了，但是我们可以参考Step2中转化问题的方式，也就是说，我们想要实现移动64个盘子从A杆到C杆，我们可以将这个大问题，转化为以下等价问题

1. 如何将上面的63个盘子从原杆A移动到杆B
2. 让最下面的第64号盘子移动到目标柱子C
3. 如何将63个盘子从杆B移动到目标杆C

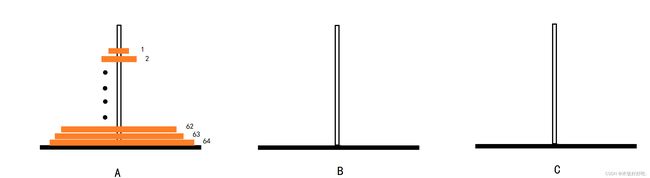
这个时候我们发现问题规模由64个盘子降低为了63个盘子，由此联想到了计算机领域的深邃思想——递归，事实上我们恰恰可以通过递归的方式实现规模的由大化小，接下来我们借助下面的图示加以理解

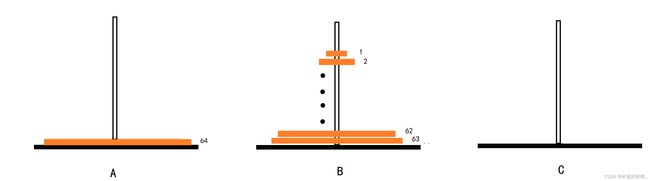
第一步：采用整体思想，将上面的63个盘子看做一个盘子，然后将其移动到辅助杆B上

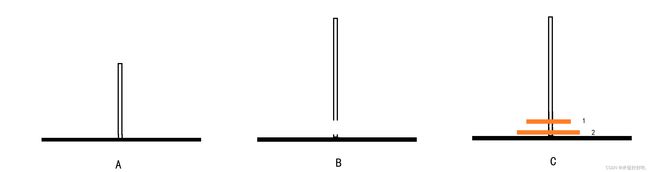
第二步：现在我们就可以将最下面的64号盘子，直接移动到目标杆C中

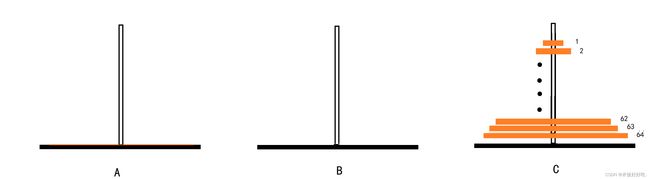
第三步：现在最后一步就是如何将63个盘子从原杆B中移动到目标杆C的过程，由此可见这是一个递归迭代的过程。

第四步：我们现在可以抽象出如何移动n个盘子从A杆到C杆的过程

1. 首先将n - 1个盘子从原杆A借助辅助杆C移动到杆B上
2. 将第n个盘子直接从原杆A移动到目标杆C上
3. 最后将n - 1个盘子从杆B借助辅助杆A移动到目标杆C上

汉诺塔代码实现

最后我们要考虑如何将递归思想转化为代码实现。递归函数设计时最重要的就是两大要件——递归出口与降低规模函数

1. 递归出口：在汉诺塔的问题中，我们不难发现，如果问题规模只有一个盘子，那么这已经是最小规模，可以直接处理，直接从待移动杆中移动到目标杆中
2. 降低规模函数：根据上面的分析，汉诺塔问题降低规模函数就是，调用递归函数，但是规模比原来要减小一个盘子

也许这样讲有点抽象，我们结合代码进行讲述

// 打印盘子移动函数
void Move(char src_pos, char dst_pos) {
	printf("%c---->%c\n", src_pos, dst_pos);
}

我们首先封装了这样一个函数，用于打印盘子的移动过程，例如我在主函数中调用Move('A', 'C')就会打印A---->C，用来模拟可视化盘子移动的过程

// 汉诺塔递归函数
void Hanoi(int num, char src_pos, char dst_pos, char help_pos) {
	if (num == 1) {
		Move(src_pos, dst_pos);
	} else {
		Hanoi(num - 1, src_pos, help_pos, dst_pos);
		Move(src_pos, dst_pos);
		Hanoi(num - 1, help_pos, dst_pos, src_pos);
	}
}

我们先来解释这个递归函数各个参数的含义：

• num：代表待移动盘子的个数
• src_pos：代表盘子原来的位置杆
• dst_pos：代表盘子的目标位置杆
• help_pos：代表盘子移动期间用来辅助移动的杆子，可以看作临时存放杆

如果我们在主函数中调用该递归函数Hanoi(3, 'A', 'C', 'B')，表明我们希望将三个盘子从原杆A移动到目标杆C，期间可以借助辅助杆B的帮助，该递归函数的出口条件为num == 1表明如果盘子规模为1，我们就直接调用Move函数进行移动，除此之外，我们就要降低问题规模，于是进入else判断分支，再次调用Hanoi(2, 'A', 'B', 'C')，这个代码对应我们之前所描述的第一步：先将2个较小盘子看做一个整体从杆A移动到杆B，然后调用Move('A', 'C')就对应我们之前所描述的第二步：将较大盘从杆A直接移动到目标杆子C，最后调用Hanoi(2, 'B', 'C', 'A')，这里就对应我们之前所描述的第三步：将B杆中的两个较小盘子看做整体再移动到目标杆C的过程

代码运行结果如上图所示，程序运行结果与我们所预期的一致，感兴趣的小伙伴也可以试试更大数量的盘子数哦！

C语言实现源代码

#include 

// 打印盘子移动函数
void Move(char src_pos, char dst_pos) {
	printf("%c---->%c\n", src_pos, dst_pos);
}

// 汉诺塔递归函数
void Hanoi(int num, char src_pos, char dst_pos, char help_pos) {
	if (num == 1) {
		Move(src_pos, dst_pos);
	} else {
		Hanoi(num - 1, src_pos, help_pos, dst_pos);
		Move(src_pos, dst_pos);
		Hanoi(num - 1, help_pos, dst_pos, src_pos);
	}
}

int main() {
	Hanoi(3, 'A', 'C', 'B');
	return 0;
}

Java语言实现源代码

public class Test {
    public static void main(String[] args) {
        hanoi(2, 'A', 'B', 'C');
    }
    // 汉诺塔递归函数
    public static void hanoi(int num, char pos1, char pos2, char pos3) {
        if (num == 1) {
            move(pos1, pos3);
            return;
        }
        // 先执行step1
        hanoi(num - 1, pos1, pos3, pos2);
        // 执行step2
        move(pos1, pos3);
        // 最后执行step3
        hanoi(num - 1, pos2, pos1, pos3);
    }
    // 移动函数
    public static void move(char pos1, char pos2) {
        System.out.printf("位置%c--->位置%c\n", pos1, pos2);
    }
}