开篇：预备知识-3

前言

我们在之前两篇文章中详细的介绍了一下 C语言的历史和关于 GCC 编译器的使用方法。这篇文章中我们来一起探讨一下关于信息数据在计算机是如何储存和表示的。有些小伙伴可能会问。数据就是储存在计算机的硬盘和主存中的啊。还能存去哪？确实，计算机中的所有数据都储存在有储存功能的部件中，这些部件包括内存、硬盘、CPU（寄存器）等。但是在这里我们要探讨的是数据在计算机中的表示形式，比如一个整型数 1 在计算机中的编码值，这是一个理论层面的东西，也可以理解为计算机科学家定制的一个标准。了解这些标准可以帮助我们更好的理解计算机的工作方式，写出更加健壮的程序。

信息表示的方法-编码

任何信息都是按照某个规则进行编码而得到的。我们日常见到的汉字、数字、英文等，当然也包括这篇文章。我们拿英语单词来举例子：

所有英语单词都是由 a~z 26 个字母中选取一个或者多个字母通过一定的顺序组合成的，这个过程就可以理解成编码：选取一个或者多个英文字母并按照一定顺序排列的过程。实际上，在这里我们把 英文字母 换成符号可能会更合适，因为从本质上来说，a~z 就是英语中 26 个用来进行信息表示的基本符号，至于为什么要采用 a~z 来作为基本符号，就得问这个语言的发明者了。

同样的，编码这个动作也适用于英语句子：所有的英语句子都是由一个或者多个英语单词按照一定的顺序组成的。

对于汉字也是一样的道理：中文中的一句话是由一个或者多个汉字组成的，而汉字又是由一个或者多个偏旁组成的。

对于不同层面的信息我们有不同的编码规则。但是只有经过了编码之后的符号才有意义。我们可以理解为：信息就是一个或者多个符号经过某个编码规则进行排列组合后得到的符号所表达的东西。

从古代的实物计数、结绳计数、筹码计数等到现代的罗马数字、阿拉伯数字，某个信息在不同的编码规则下可能有不同的符号表现。比如 ”五“ 这个数量词在罗马数字中用 V 符号表示，而在阿拉伯数字中用 5 这个符号来表示，但是它们表示的信息本质都是 五 这个数量词。

计算机中信息的编码

让我们的思绪回到现代社会。计算机帮我们 ”记住“ 和 ”做“ 了很多事情，这句话换一个描述方式是：计算机帮我们储存和处理了很多信息。而计算机内部采用 二进制 的形式来储存和处理信息。这意味着在计算机内部中，只有 0 和 1 两个符号可选。好在这两个符号数量是不受限制的。也就是说我们可以选取任意个 0 和 1 的符号进行排列组合，即编码，来得到无数个可能的结果（因为我们可以选取任意个 0 和 1）。通过这两个不同的符号已经足够描述这个世界了，只是在现实层面上我们缺少足够多的能够储存信息的介质而已，而这种介质在计算机中的最直接体现就是硬盘（无论再大，一个硬盘的容量也是有限的，容量大小时硬盘的物理属性之一）。

假设我们现在有 1 位的二进制数据，我们可以选取的二进制符号有 0 或者 1。这两我们通过排列组合得到的结果有两种可能：0、1。

如果可以选择 2 位的二进制数据呢？我们在第一位可以选择 0 或者 1，在第二位也可以选择 0 或者 1。这两我们通过排列组合得到的结果有 4 种可能性：00、01、10、11。

如果可以选择 n 位的二进制数据呢？我们通过排列组合得到的结果就有 2^n 种可能。

我们上面说过，将一个或者多个符号通过排列组合的过程就是编码。编码后的符号代表了某些信息。我们在上面已经通过二进制的符号（0 和 1）编码出了一些符号组合。但是并没有赋予其具体的含义。也就是说缺少了符号到信息的映射关系。这里的原因在于我们缺少一个实际场景，这里的缺少实际场景指的是我们还未指定这些符号要用来表示哪种类型的信息。我们来看看在计算机中这些符号组合分别代表什么信息。

信息的表示与处理

我们在上面已经知道了，编码出来的符号需要有实际的场景才可以表示对应的信息。而在计算机中这些符号表示的信息取决于这些符号被赋值给了哪种类型的变量。假设我们有一个编码出来的 8 位二进制符号：01000001，它代表的信息根据它的变量数据类型决定，我们拿 C语言中的数据类型举例子：

char

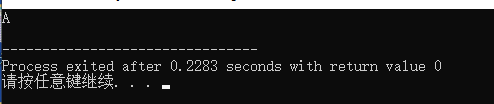
字符类型，每个变量占用 1 个字节（8位二进制）的储存空间。二进制符号范围为：00000000 ~ 11111111。一共可以有 256 个组合， 每一个值都被表示为了一个字符，对于上面的 01000001 来说。其表示的是大写字母 A，参见 [Ascii 字符对照表](#1、Ascii 码字符对照表)。我们可以通过代码验证：

#include 

int main() {
   
    // 0b 开头的代表这是一个二进制编码数据
  char c = 0b01000001;
  printf("%c\n", c);
  return 0;
} 

short

短整型类型，每个变量占用 2 个字节（16位二进制）的储存空间。二进制符号范围为 0000000000000000 ~ 1111111111111111。一共有 65536 种编码组合。 这种类型的每一种符号组合都被映射成了一个整数值。数值范围（10 进制为）：-32768 ~ 32767。至于为什么会是这个数值范围参考 整数的补码表示 小节。我们可以看到这个数值范围恰好把 short 类型的 65536 种组合用完了（-32768 ~ -1 一共 32768 用了种组合，0 ~ 32767 一共用了 32768，两个部分一共用了 65536 种组合）。

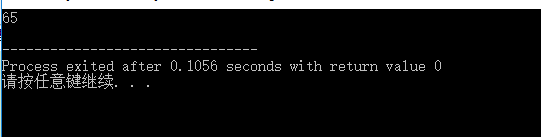
对于上面的 01000001 二进制编码符号来说，如果保存它的变量是 short 类型，那么其表示的含义是数字 65。我们可以通过代码验证：

#include 

int main() {
   
    // 0b 开头的代表这是一个二进制编码数据
  short c = 0b01000001;
  printf("%d\n", c);
  return 0;
} 

int

整型类型，在 64 位计算机上，每个变量占用 4 个字节（32位二进制）的储存空间，32 位计算机上（基本已经很少了），每个变量占用 2 个字节的储存空间（16 位二进制）。如果在 32 位机器上，这个类型就等价于 short 类型。我们这里只讨论 64 位计算机。其二进制符号范围为 00000000000000000000000000000000 ~ 11111111111111111111111111111111。一共有 4294967296 种编码组合。

和 short 类型类似，int 类型的每一个符号组合也被映射成了一个整数值。数值范围（10 进制为）：-2147483648 ~ 2147483647。所有数字的个数总和正好等于 4294967296，将 4294967296 种二进制编码的总和用完了。

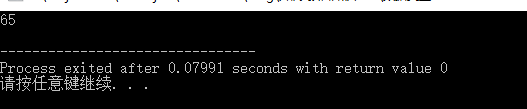
和 short 类型 一样，对于上面的 01000001 二进制编码符号来说，如果保存它的变量是 int 类型，那么其表示的含义是数字 65。我们可以通过代码验证：

#include 

int main() {
   
    // 0b 开头的代表这是一个二进制编码数据
  int c = 0b01000001;
  printf("%d\n", c);
  return 0;
} 

long

长整型，每个变量占用 4 个字节（32位二进制）的储存空间。既然它是占用 4 个字节的储存空间，同时表示的信息又是整型数值类型，那么它的功能就和 int 一模一样（二进制符号范围一样、每个符号代表的信息也一样）。即可以理解为 long 类型是 int 类型的另一个别名。那么既然两个类型功能一样，还要新建一个重复功能但又名字不同的数据类型干嘛呢？我们这里讨论的类型占用储存空间的大小全部是针对 64 位机器而言的。而对于 32 位机器而言，int 类型变量占用的字节数为 2 个字节（16位二进制）。因此在早期（32位）计算机中，long 类型是为了描述 4 个字节的整型值而存在，而随着计算机的发展，到 64 位机器之后，int 类型的变量占用的字节数也变成了 4，因此这里 int 和 long 两种数据类型的功能就重合了。

long long

双长整型，每个变量占用 8 个字节（64位二进制）的储存空间，其二进制符号范围为 0000000000000000000000000000000000000000000000000000000000000000 ~ 1111111111111111111111111111111111111111111111111111111111111111。 一共有 1.8446744073709552e+19 种编码组合。

和 int 类型类似，long long 类型的每一个符号组合也被映射成了一个整数值。数值范围（10 进制为）：-9.223372036854776e+18 ~ 9.223372036854776e+18 - 1。所有数字的个数总和正好等于 1.8446744073709552e+19，将 1.8446744073709552e+19 种二进制编码的总和用完了。

和 int 类型 一样，对于上面的 01000001 二进制编码符号来说，如果保存它的变量是 long long 类型，那么其表示的含义是数字 65。我们可以通过代码验证：

#include 

int main() {
   
    // 0b 开头的代表这是一个二进制编码数据
  long long c = 0b01000001;
  printf("%d\n", c);
  return 0;
}

float

单精度浮点类型。每个变量占用 4 个字节（32 位二进制）的储存空间。二进制符号范围为：00000000000000000000000000000000 ~ 11111111111111111111111111111111 。你会发现和 int 类型的二进制符号范围一致，其实这个很好理解，因为都是用二进制来进行编码，占用的二进制位数（都是32）也一样，自然最后编码得到的符号范围和总数也一样。那么它们的区别在哪？其实就是对每个二进制编码出来的符号赋予的含义不同：在 int 类型中，每一个二进制符号都被表示成了一个整数，而在 float 类型中，每一个二进制符号都被表示成了一个浮点数。

对于上面的 01000001 二进制编码符号来说，如果保存它的变量是 float 类型，那么其表示的含义是一个小于 1 的浮点数。我们可以通过代码验证：

#include 

int main() {
   
    // 0b 开头的代表这是一个二进制编码数据
  int c = 0b01000001;
  float *cp = (float *)&c;
  // %.128f 表示输出一个浮点数，结果保留 128 位小数
  printf("%.128f\n", *cp);
  return 0;
} 

我们需要解释一下上面的代码：我们先将 01000001 二进制编码数据赋值给了一个 int 类型的变量 c。此时变量 c 在内存中的二进制编码表示为：00000000000000000000000001000001 。即（01000001）前面补齐了 24 个 0 位（int 类型占用 32 位二进制储存空间，当给定的二进制符号位数不足 32 位时，会在左边用 0 补齐剩下的位数）。然后，我们将 c 的地址强制转换成了 float 类型的指针，最后以 float 类型的编码解释模式输出了这个二进制编码数据代表的值。关于最后打印出来的结果为什么是截图上的小数值，可以参考 浮点数的表示 小节。

为什么不直接使用 float c = 0b01000001; 来给 float 类型变量赋值呢？因为如果这样写，那么这个数据就会先转换为 int 类型，也就是 10 进制的 65，然后再将 10进制的 65 这个值转换为对应的浮点数。而最终解码出来的值还是 65 这个数字。换句话来说 float c = 0b01000001; 写法和 float c = 65; 写法是没有区别的。采用这种写法时，这个 float 变量在计算机内容实际储存的二进制编码数据就不是 0b(24 个0)01000001 了。我们可以通过下面这段代码看一下当我们使用 float c = 0b01000001; 这种赋值方式时在内存中变量 c 的二进制编码数据：