吴恩达【深度学习】笔记03——深层神经网络(Deep Neural Networks)
文章目录
-
-
- 一、深层神经网络(Deep L-layer neural network)
- 二、前向传播和反向传播(Forward and backward propagation)
-
- 1. Forward propagation
- 2. Backward propagation
- 3. Building blocks of deep neural networks
- 三、核对矩阵的维数(Getting your matrix dimensions right)
- 四、为什么使用深层表示?(Why deep representations?)
- 五、参数VS超参数(Parameters vs Hyperparameters)
-
- 1. 什么是超参数?
- 2. 如何寻找超参数的最优值?
- 六、深度学习和大脑的关联性(What does this have to do with the brain?)
- 总结
-
一、深层神经网络(Deep L-layer neural network)
目前为止学习了只有一个单独隐藏层的神经网络的正向传播和反向传播,还有逻辑回归,并且还学到了向量化,这在随机初始化权重时是很重要。本周所要做的是把这些理念集合起来,就可以执行自己的深度神经网络。首先简单复习一下前几周的内容。
1.逻辑回归

2.只拥有一个隐藏层的神经网络

神经网络层数的定义方式: 从左至右,由0开始定义。比如上面的图, x 1 x_1 x1、 x 2 x_2 x2、 x 3 x_3 x3这层是第0层,这层右边的隐藏层是第一层,由此类推。

命名规则上,一般只参考隐藏层个数和输出层。例如,上图中的逻辑回归又叫1 layer NN,1个隐藏层的神经网络叫做2 layer NN,2个隐藏层的神经网络叫做3 layer NN,以此类推。如果是L-layer NN,则包含了L-1个隐藏层,最后的L层是输出层。
下面以一个4层神经网络为例来介绍关于神经网络的一些标记写法。

输入层是第 0 0 0 层,输出层是第 L L L 层。

最后附上:深度学习符号指南。
二、前向传播和反向传播(Forward and backward propagation)
之前我们学习了构成深度神经网络的基本模块,比如每一层都有前向传播步骤以及一个相反的反向传播步骤,接下来我们要介绍如何实现这些步骤。
1. Forward propagation
Input a a a [ l − 1 ] [l-1] [l−1]
Output a a a [ l ] [l] [l], c a c h e cache cache( z z z [ l ] [l] [l])
前向传播的步骤可以写成: z z z [ l ] [l] [l] = W W W [ l ] [l] [l] · a a a [ l − 1 ] [l-1] [l−1] + b b b [ l ] [l] [l] ——> a a a [ l ] [l] [l] = g g g [ l ] [l] [l]( z z z [ l ] [l] [l])
向量化的实现过程可以写为: z z z [ l ] [l] [l] = W W W [ l ] [l] [l] · A A A [ l − 1 ] [l-1] [l−1] + b b b [ l ] [l] [l] ——> A A A [ l ] [l] [l] = g g g [ l ] [l] [l]( Z Z Z [ l ] [l] [l])
前向传播需要使用 A A A [ 0 ] [0] [0]也就是 X X X 来初始化,初始化的是第一层的输入值。 a a a [ 0 ] [0] [0]对应于一个训练样本的输入特征,而 A A A [ 0 ] [0] [0]对应于一整个训练样本的输入特征。这就是这条链的第一个前向函数的输入,重复这个步骤就可以从左到右计算前向传播。
2. Backward propagation
输入是 d a da da [ l ] [l] [l],输出是 d a da da [ l − 1 ] [l-1] [l−1], d w dw dw [ l ] [l] [l], d b db db [ l ] [l] [l]。其表达式如下:

式子(5)由式子(4)带入式子(1)得到,前四个式子就可实现反向函数。
第5个式子非常重要,它反映了 d z dz dz [ l + 1 ] [l+1] [l+1] 与 d z dz dz [ l ] [l] [l] 的递推关系。
![]()
3. Building blocks of deep neural networks
下面用流程块图来解释神经网络正向传播和反向传播过程。
如下图所示,对于第 l l l 层来说,正向传播过程中:

反向传播过程中:
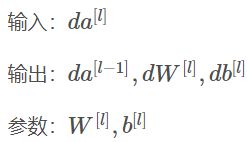
下图展示第 l l l 层的流程块图:

对于神经网络所有层,整体的流程块图正向传播过程和反向传播过程如下所示:

第一层可能使用的是ReLU激活函数,第二层为另一个ReLU激活函数,第三层可能是sigmoid函数(如果做二分类的话),输出值为 a a a [ l ] [l] [l],用来计算损失。这样就可以向后迭代通过反向传播求导来求 d w dw dw [ 3 ] [3] [3], d b db db [ 3 ] [3] [3], d w dw dw [ 2 ] [2] [2], d b db db [ 2 ] [2] [2], d w dw dw [ 1 ] [1] [1], d b db db [ 1 ] [1] [1]。在计算的时候,缓存会把 z z z [ 1 ] [1] [1], z z z [ 2 ] [2] [2], z z z [ 3 ] [3] [3] 传递过来,然后回传 d a da da [ 2 ] [2] [2], d a da da [ 1 ] [1] [1],也可以用来计算 d a da da [ 0 ] [0] [0],但通常我们不会使用它。上文讲述了一个三层网络的前向和反向传播过程。
【吴恩达老师建议】补补微积分和线性代数,多推导,多实践。
三、核对矩阵的维数(Getting your matrix dimensions right)
对于单个训练样本,输入 x x x 的维度是 (n [ 0 ] [0] [0],1)。神经网络的参数 W W W [ l ] [l] [l] 和 b b b [ l ] [l] [l] 的维度分别为:

反向传播中涉及到的矩阵的维度为:
d w dw dw [ l ] [l] [l] 和 w w w [ l ] [l] [l] 维度相同, d b db db [ l ] [l] [l] 和 b b b [ l ] [l] [l] 维度相同,且 w w w 和 b b b 向量化维度不变,但 z 、 a z、a z、a 以及 x x x 的维度向量化后会发生变化。
四、为什么使用深层表示?(Why deep representations?)
我们都知道神经网络能处理很多问题,而且效果显著。其强大能力主要源自神经网络足够“深”,也就是说网络层数越多,神经网络就更加复杂和深入,学习也更加准确。接下来,我们从几个例子入手,看一下为什么深度网络能够如此强大。
先来看人脸识别的例子,如下图所示。经过训练,神经网络第一层所做的事就是从原始图片中提取出人脸的轮廓与边缘,即边缘检测。这样每个神经元得到的是一些边缘信息。神经网络第二层所做的事情就是将前一层的边缘进行组合,组合成人脸一些局部特征,比如眼睛、鼻子、嘴巴等。再往后面,就将这些局部特征组合起来,融合成人脸的模样。可以看出,随着层数由浅到深,神经网络提取的特征也是从边缘到局部特征到整体,由简单到复杂。 可见,如果隐藏层足够多,那么能够提取的特征就越丰富、越复杂,模型的准确率就会越高。
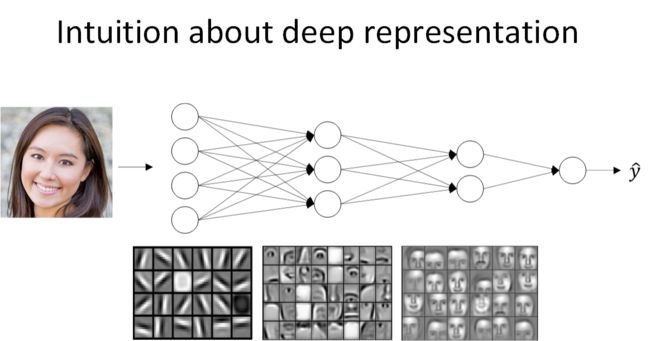
语音识别模型也是这个道理。浅层的神经元能够检测一些简单的音调,然后较深的神经元能够检测出基本的音素,更深的神经元就能够检测出单词信息。如果网络够深,还能对短语、句子进行检测。记住一点,神经网络从左到右,神经元提取的特征从简单到复杂。特征复杂度与神经网络层数成正相关。特征越来越复杂,功能也越来越强大。
除了从提取特征复杂度的角度来说明深层网络的优势之外,深层网络还有另外一个优点,就是能够减少神经元个数,从而减少计算量。例如下面这个例子,使用电路理论,计算逻辑输出:
![]()
其中,⊕表示异或操作。
对于这个逻辑运算,如果使用深度网络,深度网络的结构是每层将前一层的两两单元进行异或,最后到一个输出,如下图左边所示。这样,整个深度网络的层数是 l o g 2 ( n ) log_2(n) log2(n),不包含输入层。总共使用的神经元个数为:
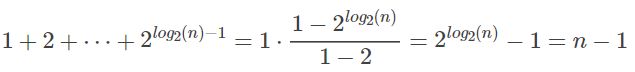
可见,输入个数是n,这种深层网络所需的神经元个数仅仅是n-1个。
如果不用深层网络,仅仅使用单个隐藏层,那么需要的神经元个数将是指数级别那么大。
比较下来,处理同一逻辑问题,深层网络所需的神经元个数比浅层网络要少很多。这也是深层神经网络的优点之一。
尽管深度学习有着非常显著的优势,Andrew还是建议对实际问题进行建模时,尽量先选择层数少的神经网络模型,这也符合奥卡姆剃刀定律(Occam’s Razor)。对于比较复杂的问题,再使用较深的神经网络模型。
五、参数VS超参数(Parameters vs Hyperparameters)
想要你的深度神经网络起很好的效果,你还需要规划好你的参数以及超参数。该部分介绍神经网络中的参数(parameters)和超参数(hyperparameters)的概念。
1. 什么是超参数?
神经网络中的参数就是我们熟悉的 W W W [ l ] [l] [l] 和 b b b [ l ] [l] [l]。
而超参数则是例如学习速率 α α α,训练迭代次数 N N N,神经网络层数 L L L,各层神经元个数 n n n [ l ] [l] [l],激活函数 g ( z ) g(z) g(z)等。之所以叫做超参数的原因是它们决定了参数 W W W [ l ] [l] [l] 和 b b b [ l ] [l] [l]的值。在后面的第二门课我们还将学习其它的超参数,这里先不讨论。
如何设置最优的超参数是一个比较困难的、需要经验知识的问题。通常的做法是选择超参数一定范围内的值,分别代入神经网络进行训练,测试cost function随着迭代次数增加的变化,根据结果选择cost function最小时对应的超参数值。这类似于validation的方法。
2. 如何寻找超参数的最优值?
进行 Idea—Code—Experiment—Idea 这个循环,尝试各种不同的参数,实现模型并观察是否成功,然后再迭代。
但参数设定这个领域,深度学习研究还在进步中,所以可能过段时间就会有更好的方法决定超参数的值,也很有可能由于CPU、GPU、网络和数据都在变化,这样的指南可能只会在一段时间内起作用,只要你不断尝试,并且尝试保留交叉检验或类似的检验方法,然后挑一个对你的问题效果比较好的数值。
近来受深度学习影响,很多领域发生了变化,从计算机视觉到语音识别到自然语言处理到很多结构化的数据应用,比如网络广告、网页搜索、产品推荐等等;有些同一领域设置超参数的直觉可以推广,但有时又不可以,特别是那些刚开始研究新问题的人们应该去尝试一定范围内的结果如何,甚至那些用了很久的模型得学习率或是其他超参数的最优值也有可能会改变。
在下个课程我们会用系统性的方法去尝试各种超参数的取值。有一条经验规律:经常试试不同的超参数,勤于检查结果,看看有没有更好的超参数取值,你将会得到设定超参数的直觉。
六、深度学习和大脑的关联性(What does this have to do with the brain?)
深度学习和大脑有什么关联性吗?——关联不大。
神经网络实际上可以分成两个部分:正向传播过程和反向传播过程。神经网络的每个神经元采用激活函数的方式,类似于感知机模型。这种模型与人脑神经元是类似的,可以说是一种非常简化的人脑神经元模型。如下图所示,人脑神经元可分为树突、细胞体、轴突三部分。树突接收外界电刺激信号(类比神经网络中神经元输入),传递给细胞体进行处理(类比神经网络中神经元激活函数运算),最后由轴突传递给下一个神经元(类比神经网络中神经元输出)。
值得一提的是,人脑神经元的结构和处理方式要复杂的多,神经网络模型只是非常简化的模型。人脑如何进行学习?是否也是通过反向传播和梯度下降算法现在还不清楚,可能会更加复杂。这是值得生物学家探索的事情。也许发现重要的新的人脑学习机制后,让我们的神经网络模型抛弃反向传播和梯度下降算法,能够实现更加准确和强大的神经网络模型!

总结
本节课主要介绍了深层神经网络,是上一节浅层神经网络的拓展和归纳。首先,我们介绍了建立神经网络模型一些常用的标准的标记符号。然后,用流程块图的方式详细推导正向传播过程和反向传播过程的输入输出和参数表达式。我们也从提取特征复杂性和计算量的角度分别解释了深层神经网络为什么优于浅层神经网络。接着,我们介绍了超参数的概念,解释了超参数与参数的区别。最后,我们将神经网络与人脑做了类别,人工神经网络是简化的人脑模型。
参考文章:redstonewill