机器学习-numpy

机器学习–numpy

Numpy（Numerical Python）是一个开源的Python科学计算库，用于快速处理任意维度的数组。

Numpy支持常见的数组和矩阵操作。对于同样的数值计算任务，使用Numpy比直接使用Python要简洁的多。

Numpy使用ndarray对象来处理多维数组，该对象是一个快速而灵活的大数据容器。

更详细的Numpy教程：NumPy 教程 | 菜鸟教程 (runoob.com)

ndarray介绍

使用Python列表可以存储一维数组，通过列表的嵌套可以实现多维数组，那么为什么还需要使用Numpy的ndarray呢？

在这里我们通过一段代码运行来体会到ndarray的好处

import random
import time
import numpy as np
a = []
for i in range(100000000):
	a.append(random.random())
# 通过%time魔法方法, 查看当前行的代码运行一次所花费的时间
%time sum1=sum(a)
b=np.array(a)
%time sum2=np.sum(b)

在结果中发现，通过numpy计算后的时间比原生python要快很多。

从中我们看到ndarray的计算速度要快很多，节约了时间。

机器学习的最大特点就是大量的数据运算，那么如果没有一个快速的解决方案，那可能现在python也在机器学习领域达不到好的效果。

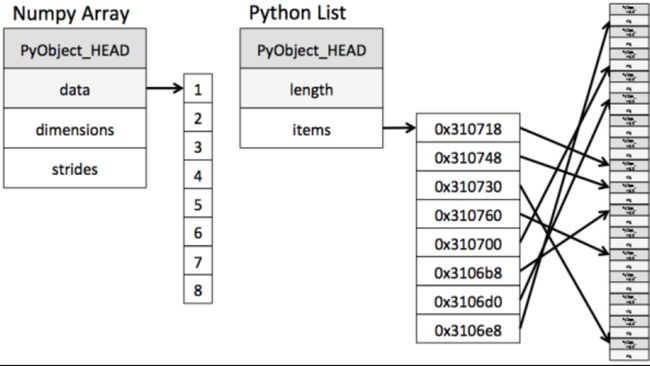
numpy和原生python的储存

简单说，ndarry储存数据与数据地址都是连续的，相比于原生python省去了寻址的时间，可以省掉很多循环语句的执行时间。

ndarray属性

NumPy 数组的维数称为秩（rank），秩就是轴的数量，即数组的维度，一维数组的秩为 1，二维数组的秩为 2，以此类推。

在 NumPy中，每一个线性的数组称为是一个轴（axis），也就是维度（dimensions）。比如说，二维数组相当于是两个一维数组，其中第一个一维数组中每个元素又是一个一维数组。所以一维数组就是 NumPy 中的轴（axis），第一个轴相当于是底层数组，第二个轴是底层数组里的数组。而轴的数量——秩，就是数组的维数。

很多时候可以声明 axis。axis=0，表示沿着第 0 轴进行操作，即对每一列进行操作；axis=1，表示沿着第1轴进行操作，即对每一行进行操作。

NumPy 的数组中比较重要 ndarray 对象属性有：

属性	说明
ndarray.ndim	秩，即轴的数量或维度的数量
ndarray.shape	数组的维度，对于矩阵，n 行 m 列
ndarray.size	数组元素的总个数，相当于 .shape 中 n*m 的值
ndarray.dtype	ndarray 对象的元素类型
ndarray.itemsize	ndarray 对象中每个元素的大小，以字节为单位

NumPy 创建数组

numpy.empty

numpy.empty 方法用来创建一个指定形状（shape）、数据类型（dtype）且未初始化的数组：

numpy.empty(shape, dtype = float, order = 'C')

参数说明：

参数	描述
shape	数组形状
dtype	数据类型，可选
order	有"C"和"F"两个选项,分别代表，行优先和列优先，在计算机内存中的存储元素的顺序。

下面是一个创建空数组的实例：

import numpy as np 
x = np.empty([3,2], dtype = int) 
print (x)

注意 − 数组元素为随机值，因为它们未初始化。

numpy.zeros

创建指定大小的数组，数组元素以 0 来填充：

numpy.zeros(shape, dtype = float, order = 'C')

参数说明：

参数	描述
shape	数组形状
dtype	数据类型，可选
order	‘C’ 用于 C 的行数组，或者 ‘F’ 用于 FORTRAN 的列数组

import numpy as np
 
# 默认为浮点数
x = np.zeros(5) 
print(x)
 
# 设置类型为整数
y = np.zeros((5,), dtype = int) 
print(y)
 
# 自定义类型
z = np.zeros((2,2), dtype = [('x', 'i4'), ('y', 'i4')])  
print(z)

numpy.ones

创建指定形状的数组，数组元素以 1 来填充：

numpy.ones(shape, dtype = None, order = 'C')

参数说明同上

import numpy as np
 
# 默认为浮点数
x = np.ones(5) 
print(x)
 
# 自定义类型
x = np.ones([2,2], dtype = int)
print(x)

numpy.ones_like

numpy.ones_like 用于创建一个与给定数组具有相同形状的数组，数组元素以 1 来填充。

numpy.ones 和 numpy.ones_like 都是用于创建一个指定形状的数组，其中所有元素都是 1。

它们之间的区别在于：numpy.ones 可以直接指定要创建的数组的形状，而 numpy.ones_like 则是创建一个与给定数组具有相同形状的数组。

numpy.ones_like(a, dtype=None, order='K', subok=True, shape=None)

参数说明：

参数	描述
a	给定要创建相同形状的数组
dtype	创建的数组的数据类型
order	数组在内存中的存储顺序，可选值为 ‘C’（按行优先）或 ‘F’（按列优先），默认为 ‘K’（保留输入数组的存储顺序）
subok	是否允许返回子类，如果为 True，则返回一个子类对象，否则返回一个与 a 数组具有相同数据类型和存储顺序的数组
shape	创建的数组的形状，如果不指定，则默认为 a 数组的形状。

创建一个与 arr 形状相同的，所有元素都为 1 的数组：

import numpy as np
 
# 创建一个 3x3 的二维数组
arr = np.array([[1, 2, 3], [4, 5, 6], [7, 8, 9]])
 
# 创建一个与 arr 形状相同的，所有元素都为 1 的数组
ones_arr = np.ones_like(arr)
print(ones_arr)

NumPy 从已有的数组创建数组

• np.array(object, dtype)
• np.asarray(a, dtype)

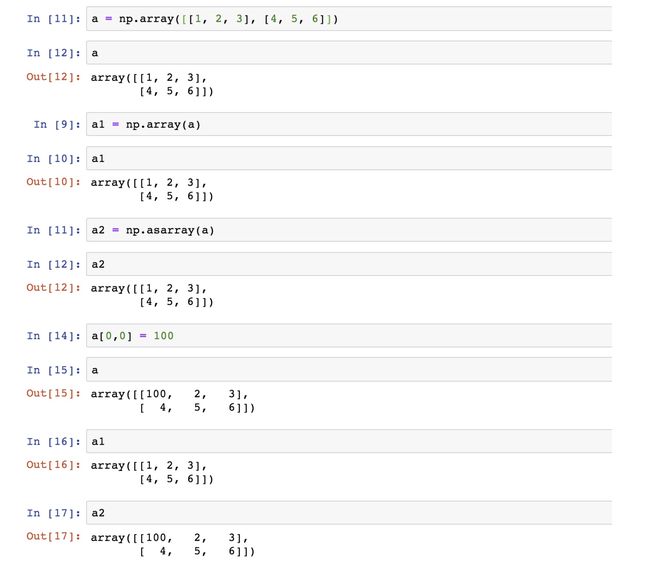
a = np.array([[1,2,3],[4,5,6]])
# 从现有的数组当中创建
a1 = np.array(a)

# 相当于索引的形式，并没有真正的创建一个新的
a2 = np.asarray(a)

两者的区别：

生成固定范围的数组

np.linspace (start, stop, num, endpoint)**

创建等差数组 — 指定数量

参数:

• start:序列的起始值
• stop:序列的终止值
• num:要生成的等间隔样例数量，默认为50
• endpoint:序列中是否包含stop值，默认为ture

# 生成等间隔的数组
np.linspace(0, 100, 11)

返回结果：
array([ 0., 10., 20., 30., 40., 50., 60., 70., 80., 90., 100.])

np.arange(start,stop, step, dtype)

• 创建等差数组 — 指定步长
• 参数
  • step:步长,默认值为1

np.arange(10, 50, 2)

返回结果：
array([10, 12, 14, 16, 18, 20, 22, 24, 26, 28, 30, 32, 34, 36, 38, 40, 42,
44, 46, 48])

np.logspace(start,stop, num)

• 创建等比数列
• 参数:
  • num:要生成的等比数列数量，默认为50

# 生成10^x
np.logspace(0, 2, 3)

返回结果:
array([ 1., 10., 100.])

生成随机数组

使用模块介绍

• np.random模块

正态分布

正态分布是一种概率分布。正态分布是具有两个参数μ和σ的连续型随机变量的分布，第一参数μ是服从正态分布的随机变量的均值，第二个参数σ是此随机变量的标准差，所以正态分布记作N(μ，σ )

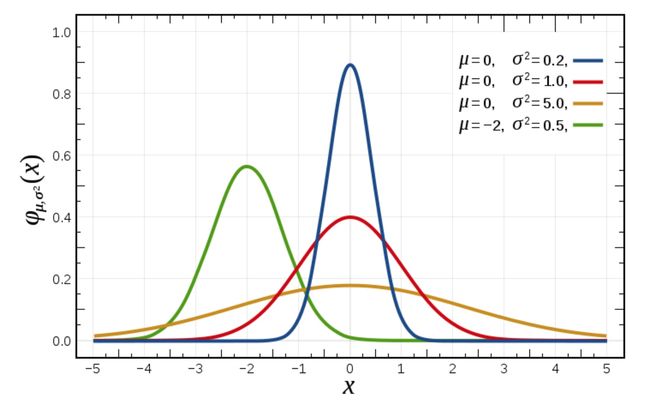
μ决定了其位置，其标准差σ决定了分布的幅度。当μ = 0,σ = 1时的正态分布是标准正态分布。

• 方差

是在概率论和统计方差衡量一组数据时离散程度的度量

$${\sigma }^2=\frac{(x_1-M{)}^2+(x_2-M{)}^2+(x_3-M{)}^2+\dots \dots (x_n-M{)}^2}{n}$$

其中M为平均值，n为数据总个数，σ 为标准差，σ ^2可以理解一个整体为方差

$\sigma =\sqrt{\frac{1}{N}{\sum }_{i=1}^N{(x_i-\mu )}^2}$

正态分布创建方式

np.random.randn(d0, d1, …, dn)

功能：从标准正态分布中返回一个或多个样本值

• np.random.normal(loc=0.0,scale=1.0, size=None)

loc：float

此概率分布的均值（对应着整个分布的中心centre）

scale：float

此概率分布的标准差（对应于分布的宽度，scale越大越矮胖，scale越小，越瘦高）

size：int or tuple of ints

输出的shape，默认为None，只输出一个值

• np.random.standard_normal(size=None)

返回指定形状的标准正态分布的数组

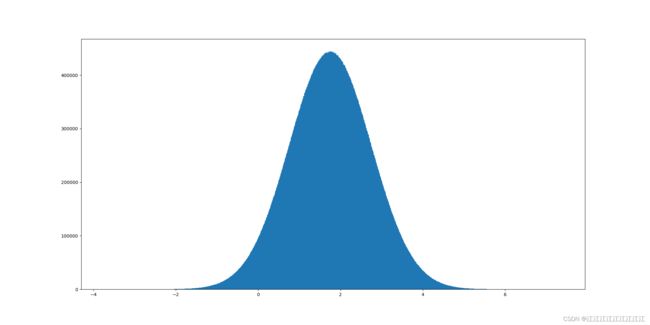
举例1：生成均值为1.75，标准差为1的正态分布数据，100000000个

x1 = np.random.normal(1.75, 1, 100000000)

# 生成均匀分布的随机数
x1 = np.random.normal(1.75, 1, 100000000)
# 画图看分布状况
# 1）创建画布
plt.figure(figsize=(20, 10), dpi=100)
# 2）绘制直方图
plt.hist(x1, 1000)
# 3）显示图像
plt.show()

举例2：随机生成4支股票1周的交易日涨幅数据

4支股票，一周**(5天)**的涨跌幅数据，如何获取？

随机生成涨跌幅在某个正态分布内，比如均值0，方差1

股票涨跌幅数据的创建

# 创建符合正态分布的4只股票5天的涨跌幅数据
stock_change = np.random.normal(0, 1, (4, 5))
stock_change

均匀分布

• np.random.rand(d0, d1, …, dn)
  • 返回[0.0，1.0)内的一组均匀分布的数。
• np.random.uniform(low=0.0,high=1.0, size=None)
  • 功能：从一个均匀分布[low,high)中随机采样，注意定义域是左闭右开，即包含low，不包含high.
  • 参数介绍:
    • low: 采样下界，float类型，默认值为0；
    • high: 采样上界，float类型，默认值为1；
    • size: 输出样本数目，为int或元组(tuple)类型，例如，size=(m,n,k), 则输出mnk个样本，缺省时输出1个值。
  • 返回值：ndarray类型，其形状和参数size中描述一致。
• np.random.randint(low, high=None, size=None, dtype=‘l’)
  • 从一个均匀分布中随机采样，生成一个整数或N维整数数组，
  • 取数范围：若high不为None时，取[low,high)之间随机整数，否则取值[0,low)之间随机整数。

# 生成均匀分布的随机数
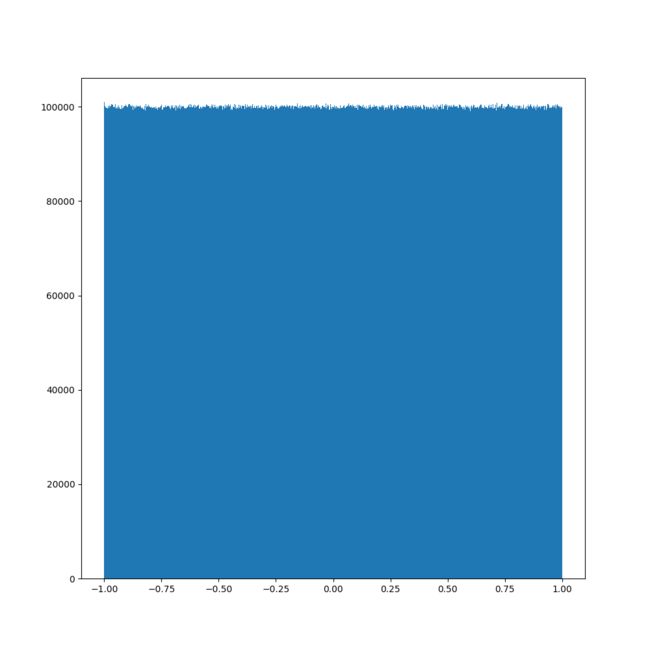
x2 = np.random.uniform(-1, 1, 100000000)

画图看分布状况：

import matplotlib.pyplot as plt
# 生成均匀分布的随机数
x2 = np.random.uniform(-1, 1, 100000000)
# 画图看分布状况
# 1）创建画布
plt.figure(figsize=(10, 10), dpi=100)
# 2）绘制直方图
plt.hist(x=x2, bins=1000) # x代表要使用的数据，bins表示要划分区间数
# 3）显示图像
plt.show()

数组的索引、切片

一维、二维、三维的数组如何索引？

• 直接进行索引,切片
• 对象[:, :] – 先行后列

二维数组索引方式：

• 举例：获取第一个股票的前3个交易日的涨跌幅数据

# 二维的数组，两个维度
stock_change[0, 0:3]

三维数组索引方式：

# 三维
a1 = np.array([ [[1,2,3],[4,5,6]], [[12,3,34],[5,6,7]]])

# 返回结果
array([[[ 1, 2, 3],
[ 4, 5, 6]],
[[12, 3, 34],
[ 5, 6, 7]]])
# 索引、切片
>>> a1[0, 0, 1] # 输出: 2

形状修改

ndarray.reshape(shape, order)

• 返回一个具有相同数据域，但shape不一样的视图

• 行、列不进行互换

# 在转换形状的时候，一定要注意数组的元素匹配
stock_change.reshape([5, 4])
stock_change.reshape([-1,10]) # 数组的形状被修改为: (2, 10), -1: 表示通过待计算

ndarray.resize(new_shape)

• 修改数组本身的形状（需要保持元素个数前后相同）
• 行、列不进行互换

stock_change.resize([5, 4])
# 查看修改后结果

stock_change.shape
(5, 4)

ndarray.T

数组的转置

• 将数组的行、列进行互换

stock_change.T.shape
(4, 5)

类型修改

ndarray.astype(type)

• 返回修改了类型之后的数组

stock_change.astype(np.int32)

ndarray.tostring([order])或者ndarray.tobytes([order])

• 构造包含数组中原始数据字节的Python字节

arr = np.array([[[1, 2, 3], [4, 5, 6]], [[12, 3, 34], [5, 6, 7]]])
arr.tostring()

数组的去重

np.unique()

temp = np.array([[1, 2, 3, 4],[3, 4, 5, 6]])

>>> np.unique(temp)
array([1, 2, 3, 4, 5, 6])

ndarray运算

逻辑运算

# 生成10名同学，5门功课的数据
>>> score = np.random.randint(40, 100, (10, 5))
# 取出最后4名同学的成绩，用于逻辑判断
>>> test_score = score[6:, 0:5]
# 逻辑判断, 如果成绩大于60就标记为True 否则为False
>>> test_score > 60
array([[ True, True, True, False, True],
[ True, True, True, False, True],
[ True, True, False, False, True],
[False, True, True, True, True]])
# BOOL赋值, 将满足条件的设置为指定的值-布尔索引
>>> test_score[test_score > 60] = 1
>>> test_score
array([[ 1, 1, 1, 52, 1],
[ 1, 1, 1, 59, 1],
[ 1, 1, 44, 44, 1],
[59, 1, 1, 1, 1]])

通用判断函数

• np.all()

# 判断前两名同学的成绩[0:2, :]是否全及格
>>> np.all(score[0:2, :] > 60)
False

• np.any()

# 判断前两名同学的成绩[0:2, :]是否有大于90分的
>>> np.any(score[0:2, :] > 80)
True

np.where（三元运算符）

通过使用np.where能够进行更加复杂的运算

• np.where()

# 判断前四名学生,前四门课程中，成绩中大于60的置为1，否则为0
temp = score[:4, :4]
np.where(temp > 60, 1, 0)

• 复合逻辑需要结合np.logical_and和np.logical_or使用

# 判断前四名学生,前四门课程中，成绩中大于60且小于90的换为1，否则为0
np.where(np.logical_and(temp > 60, temp < 90), 1, 0)

# 判断前四名学生,前四门课程中，成绩中大于90或小于60的换为1，否则为0
np.where(np.logical_or(temp > 90, temp < 60), 1, 0)

统计运算

如果想要知道学生成绩最大的分数，或者做小分数应该怎么做？

统计指标

在数据挖掘/机器学习领域，统计指标的值也是我们分析问题的一种方式。常用的指标如下：

• min(a, axis)
  • Return the minimum of an array or minimum along an axis.
• max(a, axis])
  • Return the maximum of an array or maximum along an axis.
• median(a, axis)
  • Compute the median along the specified axis.
• mean(a, axis, dtype)
  • Compute the arithmetic mean along the specified axis.
• std(a, axis, dtype)
  • Compute the standard deviation along the specified axis.
• var(a, axis, dtype)
  • Compute the variance along the specified axis.

案例：学生成绩统计运算

进行统计的时候，axis 轴的取值并不一定，Numpy中不同的API轴的值都不一样，在这里，axis 0代表列, axis 1代表行去进行统计

# 接下来对于前四名学生,进行一些统计运算
# 指定列 去统计

temp = score[:4, 0:5]
print("前四名学生,各科成绩的最大分：{}".format(np.max(temp, axis=0)))
print("前四名学生,各科成绩的最小分：{}".format(np.min(temp, axis=0)))
print("前四名学生,各科成绩波动情况：{}".format(np.std(temp, axis=0)))
print("前四名学生,各科成绩的平均分：{}".format(np.mean(temp, axis=0)))

结果：

前四名学生,各科成绩的最大分：[96 97 72 98 89]
前四名学生,各科成绩的最小分：[55 57 45 76 77]
前四名学生,各科成绩波动情况：[16.25576821 14.92271758 10.40432602 8.0311892 4.32290412]
前四名学生,各科成绩的平均分：[78.5 75.75 62.5 85. 82.25]

如果需要统计出某科最高分对应的是哪个同学？

• np.argmax(temp, axis=)

• np.argmin(temp, axis=)

print("前四名学生，各科成绩最高分对应的学生下标：{}".format(np.argmax(temp, axis=0)))

结果：

前四名学生，各科成绩最高分对应的学生下标：[0 2 0 0 1]