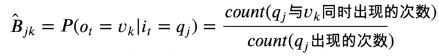HMM隐马尔可夫模型和维特比算法
前言
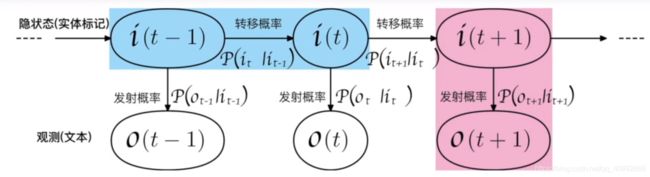
一、HMM的构成
二、HMM的基本假设
1.齐次马尔可夫假设
2.观测独立假设
3.参数不变性假设
三、HMM的参数学习(监督学习)
四、参数学习的代码思路
五、维特比算法
六、维特比算法代码思路
总结
前言
隐马尔可夫模型是关于时序的概率图模型,属于生成模型,描述由一个隐藏的马尔可夫链随机生成不可观测的状态随机序列,再由各个状态生成一个观测而产生观测随机序列的过程。
隐马尔可夫模型常用来处理诸如分词,词性标注,命名实体识别(NER)等问题序列标注问题。
一、HMM的构成
想要了解HMM的内容,首先需要知道HMM由哪几部分构成,下面我们以命名实体识别(NER)任务为例:
①假设可观测序列由所有汉字组成的集合,我们有:
![]()
其中M为可观测状态的最大数量
②设可能隐藏状态集合为所有命名实体识别对应的标签,我们有:
![]()
其中N为隐藏状态的数量
③设我们有观测到的一串序列文本和对应的实体标记:
![]()
④我们设t时刻任何一种隐状态都可以在t+1时刻转换为任何一种其他类型的实体标签,则转换路径共有N*N种,我们使用一个矩阵来表示所有可能的状态转移概率(转移概率矩阵,通常我们设其为A矩阵)
⑤由于任意时刻的观测只依赖于当前隐状态,设我们有M个汉字(M种观测值),N种实体标签(N种隐状态),则这一过程可以使用一个发射概率矩阵来表示,维度为N*M(这个矩阵一般很扁长,我们通常设为B矩阵)
⑥初始的隐状态我们一般称之为π,他是一个向量,不同维度对应第一个状态是某个隐状态的不同概率值,。
![]()
举例:新闻类实体标签第一个状态(实体标签)通常为人名或地名
那么,HMM对应的三大参数分别为④,⑤,⑥种对应的A,B,π
二、HMM的基本假设
1.齐次马尔可夫假设
第t时刻的隐状态仅与t-1时刻的隐状态有关,与其他隐状态无关
2.观测独立假设
某一时刻的观测结果仅与当前时刻的隐状态有关
3.参数不变性假设
三大要素不随时间的变化而改变,即在整个训练过程中一直保持不变
三、HMM的参数学习(监督学习)
HMM的参数学习非常简单,它更类似一种统计的过程,其背后的原理由极大似然估计支撑。
1.首先是初始隐状态π的参数估计
这里的分母由我们的数据量决定,比如我们有5000条语料,则分母为5000,分子则是不同隐状态(实体标签)对应的个数。
2.转移概率矩阵A的参数估计
这里的分子实际上对应了联合概率,分母对应了边缘概率。
3.发射概率矩阵B的参数估计
同样,这里的分子实际上对应了联合概率,分母对应了边缘概率。
四、参数学习的代码思路
①首先由于我们要获取矩阵A,B,可以提前初始化一个N*N和N*M的全零矩阵。
②对于不同状态和不同的观测值,由于我们需要将其存入矩阵,所以需要为每个状态和观测值分配索引下标,这里我们可以使用一个hash_map完成。
③遍历语料,同时获取第t时刻的状态索引i,第t时刻的观测值q,第t+1时刻的索引j,
在A矩阵中,我们将索引下标[i,j]对应元素自增1,在B矩阵中,我们将索引下标[i,q]对应元素自增1
④分别对A和B按列求均值得对应的概率,此外可以初始化一个π向量记录所有标签出现在初始位置的概率。
⑤先加上一个非常小的偏置项(防止出现log(0))再取log,以防止在计算中下溢
五、维特比算法
维特比算法的目的其实就是寻找到一条概率最大的路径,其核心思想如下:
在每一时刻,计算当前时刻落在每种隐状态的最大概率(这个隐状态作为当前时刻的最大概率路径中的最后一个结点),并记录这个最大概率是从前一时刻的哪一个隐状态转移过来的,最后再从结尾回溯最大概率,得到最有可能的最优路径。
由于涉及了状态转移,其核心算法主要依靠于动态规划。
下面我们以例子说明维特比算法:
假设我们的观测集合为:
![]()
可能的隐状态集合:
![]()
观测序列:
![]()
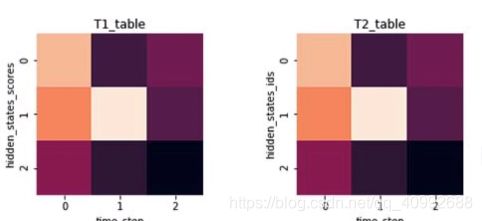
假设我们已经学习到了参数A,B,π,我们想求得最有可能的观测序列,在维特比算法中,我们需要两个表格T1,T2来暂存某时刻的最大路径概率和路径结点,其大小皆为(隐状态数*序列长度)。
计算过程:
①在动态规划中,我们首先要填入初始值,同样,维特比算法在初始时也要有对应的初始值:
初始值即当路径长度为1时,每条路径的最大概率:
那么路径长度为1的时候,实际上就是初始状态概率乘以对应的发射概率。
我们有初始状态π:
发射概率矩阵:
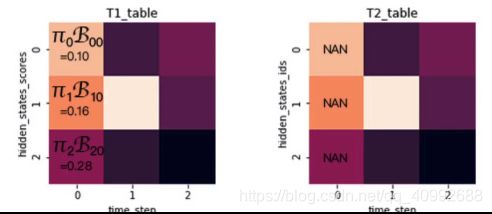
由于我们第一个生成的是V0,所以我们将对应位置向量相乘,并存储到T1和T2中:
T1记录以某状态结点为结尾的路径最大概率,T2记录这个状态是由哪里转移过来的
②下面,我们来计算t1时刻,实际上,相当于在之前的路径基础上,分别计算我们接入当前状态结点,并产生对应观测值后的最大概率
如图所示,实际上我们是在寻找接入第二个状态结点,并产生观测值后对应的最大概率的路径。
由于第1时刻的三种状态分别可能由第0时刻的三种状态转移而来,所以实际上我们在每一时刻都有N*N种状态转移概率要计算。
我们在t1表格中的第2列,要分别计算由第一列的i状态转移到第2列的j状态,在填第一行时,实际上就是乘以转移概率矩阵的第一列,再乘以对应发射矩阵概率并取最大:
举个例子说明一下,这里面第二列的第一行,实际上是由max(0.1*0.5*0.5,0.16*0.3*0.5,0.28*0.2*0.5)得来。
这里面0.1*0.5,0.16*0.3,0.28*0.2分别对应仅求接上状态0结点后的最大概率,
我们还要对应乘上状态0生成观测值V1的概率0.5得到最终结果。
③表格中填满后,我们反过来求出最优路径:
这里面,我们一步步反推,直到遇到NAN终止。
于是我们得到最优路径q2,q2,q2
六、维特比算法代码思路
在正向计算最大概率的过程,我们有一个求最大概率的步骤,这里可以利用到numpy中的广播性质:
假设我们有
初始状态T1我们可以直接计算后填入T1
我们为其拓展最后一个维度
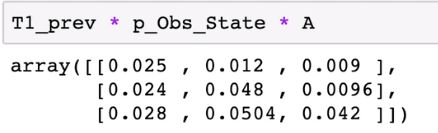
由于第一时刻的观测结果为V1,所以取B矩阵第1列,(拓展到一般:取循环遍历的第i列)并为其第0维拓展:
然后我们利用广播算法对位相乘
T1_prev*A得到的矩阵的每一列代表了状态到0,1,2的概率,然后我们对应元素乘以观测向量按行广播的矩阵,就可以得到最终值。
得到结果的每一列,实际上对应了T1每一行的转移过程的不同概率,我们只要沿着列求最大值,就可以填出每一行。
七、前向算法
前向算法用于解决HMM三大问题中的概率计算问题,这三大问题分别为:
其中预测问题和学习问题在前文中已经介绍了,下面说一下概率计算问题。
其实只要掌握了维特比算法,理解前向算法也就不难了,在维特比算法中,我们知道t时刻可能由t-1时刻的N种状态转移而来,为了保证每时的路径最大概率,我们每次取max,而在前向算法中,为了求得所有可能的情况,我们需要将上一时刻的所有状态转移到当前状态的概率累和,然后乘以对应的发射概率,当求到最后一步的时候,将所有状态的概率累和(即按行累和),就可以得到最终的概率,这种方法的时间复杂度和维特比算法持平,这比遍历算法的时间复杂度要低很多。
总结
HMM属于典型的生成模型,这里我们引用一段话