K-means聚类分析（Python）
原理
解决将空间中一些点分成K类的问题，K 代表样本类别数 Kind
先假设 K = 2 ，即要分为两类：
- 在空间中随机选定两个样本作为分类基准，计算比较其他样本与其距离，离谁近就归为哪一类。
- 迭代，找到两个样本中中心，计算中心点与其他点的距离，按照距离远近再分类。
- 重复迭代直到某次迭代结果与上次完全相同。
推广到K就是：
K均值聚类算法是先随机选取K个对象作为初始的聚类中心。然后计算每个对象与各个种子聚类中心之间的距离，把每个对象分配给距离它最近的聚类中心。聚类中心以及分配给它们的对象就代表一个聚类。每分配一个样本，聚类的聚类中心会根据聚类中现有的对象被重新计算。这个过程将不断重复直到满足某个终止条件。终止条件可以是没有（或最小数目）对象被重新分配给不同的聚类，没有（或最小数目）聚类中心再发生变化，误差平方和局部最小。
K-means基于这样的假设：
特征空间中相近的两个样本，很可能同属于一个类别。
这种通过分析数据在空间中的分布状况进行分类的方法，称为聚类
Python代码
import numpy as np
# 1 读数据
# （这里先创建一个明显分为2类20*2的例子（每一列为一个变量共2个变量，每一行为一个样本共20个样本））
c1x = np.random.uniform(0.5, 1.5, (1, 10))
c1y = np.random.uniform(0.5, 1.5, (1, 10))
c2x = np.random.uniform(3.5, 4.5, (1, 10))
c2y = np.random.uniform(3.5, 4.5, (1, 10))
x = np.hstack((c1x, c2x))
y = np.hstack((c1y, c2y))
X = np.vstack((x, y)).T
print(X)
# 2 引用Python库将样本分为两类（k=2）
import matplotlib.pyplot as plt
from sklearn.cluster import KMeans
kmeans = KMeans(n_clusters=2)
result = kmeans.fit_predict(X) # 训练及预测
print(result) # 分类结果
# 3 散点图
plt.rcParams['font.family'] = ['sans-serif']
# 采用无衬线字体，通常在数据可视化中使用
x = [i[0] for i in X]
y = [i[1] for i in X]
plt.scatter(x, y, c=result, marker='o')
plt.xlabel('x')
plt.ylabel('y')
plt.show()
出现警告
FutureWarning: The default value of
n_initwill change from 10 to 'auto' in 1.4. Set the value ofn_initexplicitly to suppress the warning super()._check_params_vs_input(X, default_n_init=10)
这个警告指出，n_init 参数的默认值将在将来的版本中从 10 更改为 'auto'。为了抑制这个警告，建议在创建 KMeans 对象时明确设置 n_init 参数的值。
n_init 参数表示 K 均值算法执行的初始化次数，每次都使用不同的随机初始中心。选择最好的聚类结果作为最终结果。将其设置为 'auto' 表示根据数据样本大小自动选择初始化次数。
于是可以这样设置 n_init 参数：
kmeans = KMeans(n_clusters=2, n_init=10) # 或者选择其他合适的值 result = kmeans.fit_predict(X)K不确定
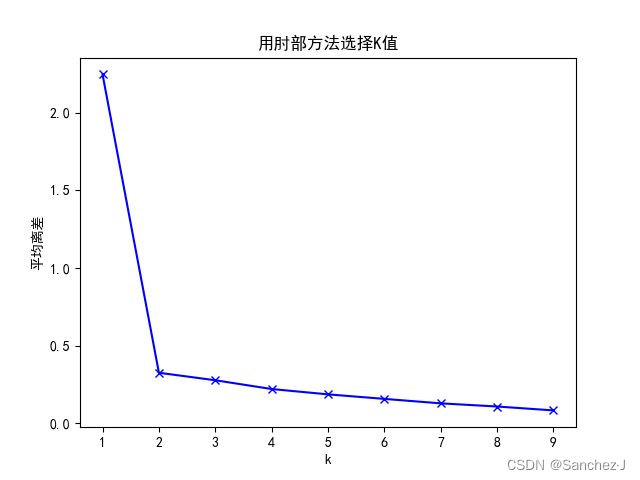
如果K值未知，可采用肘部法选择K值：假设最大分类数为9类，分别计算分类结果为1-9类的平均离差，离差的提升变化下降最抖时的值为最优聚类数K
平均离差
平均离差（Mean Absolute Deviation，简称MAD）是一种测量数据集中各数据点与数据集均值之间差异的统计指标。
计算方法如下：
- 计算每个数据点与数据集均值的差值（绝对值）。
- 对所有差值取平均值，得到平均离差。
具体公式如下：
其中：
- ( MAD ) 是平均离差。
- ( n ) 是数据集中的数据点数量。
- (
) 是第 ( i ) 个数据点。 - (
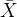) 是数据集的均值。
平均离差的值越小，表示数据点相对于均值的差异越小，数据集越集中。相反，较大的平均离差值可能表示数据集中的数据点较分散。
肘部方法
肘部方法（Elbow Method）是一种在聚类分析中用于确定最佳聚类数目的启发式方法。它的基本思想是随着聚类数目的增加，样本划分会更精细，每个簇的聚合度更高，因此每个簇的平均离差（或其他聚类评估指标）会减小。然而，当簇数目达到真实聚类数时，增加簇的数量对平均离差的改善会减缓，形成一个肘部。
肘部方法的步骤通常包括：
- 对于不同的聚类数目（k值），使用聚类算法计算相应的聚类结果。
- 对每个聚类结果计算聚类评估指标，例如平均离差。
- 绘制聚类数目与聚类评估指标的关系图。
- 观察图形中的"肘部"，即图形开始减缓的位置。这个位置对应的聚类数目被认为是最佳的聚类数。
通常，肘部方法是一个经验性的技术，不是一种精确的数学方法。在实践中，肘部方法对于一些数据集可以提供有效的线索，但对于其他数据集可能效果不佳。
Python代码
# 如果K值未知，可采用肘部法选择K值（假设最大分类数为9类，分别计算分类结果为1 - 9类的平均离差，
# 离差的提升变化下降最抖时的值为最优聚类数K）
import matplotlib.pyplot as plt
from sklearn.cluster import KMeans
from scipy.spatial.distance import cdist
K = range(1, 10)
meanDispersions = []
for k in K:
kmeans = KMeans(n_clusters=k, n_init=10)
kmeans.fit(X)
# 计算平均离差
m_Disp = sum(np.min(cdist(X, kmeans.cluster_centers_, 'euclidean'), axis=1)) / X.shape[0]
meanDispersions.append(m_Disp)
plt.rcParams['font.family'] = ['sans-serif']
plt.rcParams['font.sans-serif'] = ['SimHei'] # 使折线图显示中文
plt.plot(K, meanDispersions, 'bx-')
plt.xlabel('k')
plt.ylabel('平均离差')
plt.title('用肘部方法选择K值')
plt.show()关于其中这一句的解释
m_Disp = sum(np.min(cdist(X, kemans.cluster_centers_, 'euclidean'), axis=1)) / X.shape[0]-
cdist(X, kmeans.cluster_centers_, 'euclidean')：使用cdist函数计算数据集X中每个数据点到 K 均值聚类中心的欧氏距离。这个函数返回一个矩阵，其中第 i 行和第 j 列的元素表示第 i 个数据点到第 j 个聚类中心的距离。 -
np.min(cdist(X, kmeans.cluster_centers_, 'euclidean'), axis=1)：在上述距离矩阵中沿着第二个轴（axis=1）找到每行的最小值，即每个数据点到其所属聚类中心的最小欧氏距离。 -
sum(np.min(cdist(X, kmeans.cluster_centers_, 'euclidean'), axis=1))：对所有最小距离进行求和，得到总的最小距离。 -
/ X.shape[0]：X.shape[0]是 NumPy 数组X的形状（shape）属性中的第一个元素，表示数据集X的行数，也就是数据点的数量。这里将总的最小距离除以数据集中数据点的数量，得到平均离差。
结果
完整代码
import numpy as np
# 1 读数据
# （这里先创建一个明显分为2类20*2的例子（每一列为一个变量共2个变量，每一行为一个样本共20个样本））
c1x = np.random.uniform(0.5, 1.5, (1, 10))
c1y = np.random.uniform(0.5, 1.5, (1, 10))
c2x = np.random.uniform(3.5, 4.5, (1, 10))
c2y = np.random.uniform(3.5, 4.5, (1, 10))
x = np.hstack((c1x, c2x))
y = np.hstack((c1y, c2y))
X = np.vstack((x, y)).T
print(X)
# 2 引用Python库将样本分为两类（k=2）
import matplotlib.pyplot as plt
from sklearn.cluster import KMeans
kmeans = KMeans(n_clusters=2, n_init=10)
result = kmeans.fit_predict(X) # 训练及预测
print(result) # 分类结果
# 3 散点图
plt.rcParams['font.family'] = ['sans-serif']
# 采用无衬线字体，通常在数据可视化中使用
x = [i[0] for i in X]
y = [i[1] for i in X]
plt.scatter(x, y, c=result, marker='o')
plt.xlabel('x')
plt.ylabel('y')
plt.show()
# 如果K值未知，可采用肘部法选择K值（假设最大分类数为9类，分别计算分类结果为1 - 9类的平均离差，
# 离差的提升变化下降最抖时的值为最优聚类数K）
import matplotlib.pyplot as plt
from sklearn.cluster import KMeans
from scipy.spatial.distance import cdist
K = range(1, 10)
meanDispersions = []
for k in K:
kmeans = KMeans(n_clusters=k, n_init=10)
kmeans.fit(X)
# 计算平均离差
m_Disp = sum(np.min(cdist(X, kmeans.cluster_centers_, 'euclidean'), axis=1)) / X.shape[0]
meanDispersions.append(m_Disp)
plt.rcParams['font.family'] = ['sans-serif']
plt.rcParams['font.sans-serif'] = ['SimHei'] # 使折线图显示中文
plt.plot(K, meanDispersions, 'bx-')
plt.xlabel('k')
plt.ylabel('平均离差')
plt.title('用肘部方法选择K值')
plt.show()