学习总结2
# [USACO1.5] 八皇后 Checker Challenge
## 题目描述
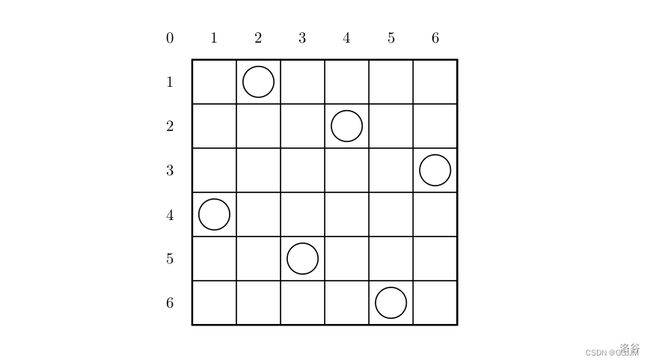
一个如下的 6 * 6 的跳棋棋盘,有六个棋子被放置在棋盘上,使得每行、每列有且只有一个,每条对角线(包括两条主对角线的所有平行线)上至多有一个棋子。
上面的布局可以用序列 2 4 6 1 3 5 来描述,第 i 个数字表示在第 i 行的相应位置有一个棋子,如下:
行号 1 2 3 4 5 6
列号 2 4 6 1 3 5
这只是棋子放置的一个解。请编一个程序找出所有棋子放置的解。
并把它们以上面的序列方法输出,解按字典顺序排列。
请输出前 3 个解。最后一行是解的总个数。
## 输入格式
一行一个正整数 n,表示棋盘是 n * n 大小的。
## 输出格式
前三行为前三个解,每个解的两个数字之间用一个空格隔开。第四行只有一个数字,表示解的总数。
## 样例 #1
### 样例输入 #1
```
6
```
### 样例输出 #1
```
2 4 6 1 3 5
3 6 2 5 1 4
4 1 5 2 6 3
4
```
## 提示
【数据范围】
对于 100% 的数据,6 <= n <= 13。
题目翻译来自NOCOW。
USACO Training Section 1.5
解题思路
使用dfs对棋盘进行枚举找出所有可能的结果。因为每一个皇后都要独占一行一列和两条对角线,所以每一个皇后落座后都要为他所在的行、列和两条对角线做记号使得后来的皇后无法落座。行和列标记好打,两条对角线如何标记呢,通过观察(看讲解知道是通过同一个斜率得出来的)可以发现他有一条对角线x+y是相等的,另一条对角线的x-y是相等的,通过这个规律就可以轻易地为对角线做标记。
代码
#include
#include
using namespace std;
int g[20];
int j[20]; //列标记
int d[1000]; //一条对角线
int d1[1000]; //另一条对角线
int a[14]; //记住所在的列
int n,k=0; //k用于记录一共有几种摆法
int dfs(int h)
{
int x,z,y;
if(h==n+1)
{
k++; //将k自加
if(k<=3)
{
for(x=1;x<=n;x++)
printf("%d ",a[x]);
printf("\n");
}
return 0;
}
else
{
for(x=1;x<=n;x++)
{
if(d[h+x]==0&&d1[h-x+n]==0&&j[x]==0) //如果列和对角线都没有被标记就落座
{
a[h]=x;
d[h+x]=1;
d1[h-x+n]=1; //加n是为了使下标不为负数
j[x]=1;
dfs(h+1);
d[h+x]=0;
d1[h-x+n]=0;
j[x]=0;
}
}
}
return 0;
}
int main()
{
scanf("%d",&n);
dfs(1);
printf("%d",k);
return 0;
}
# kkksc03考前临时抱佛脚
## 题目背景
kkksc03 的大学生活非常的颓废,平时根本不学习。但是,临近期末考试,他必须要开始抱佛脚,以求不挂科。
## 题目描述
这次期末考试,kkksc03 需要考 4 科。因此要开始刷习题集,每科都有一个习题集,分别有 s1,s2,s3,s4 道题目,完成每道题目需要一些时间,可能不等(A1,A2,...,As1,B1,B2,...,Bs2,C1,C2,....,Cs3,D1,D2,....,Ds4)。
kkksc03 有一个能力,他的左右两个大脑可以同时计算 2 道不同的题目,但是仅限于同一科。因此,kkksc03 必须一科一科的复习。
由于 kkksc03 还急着去处理洛谷的 bug,因此他希望尽快把事情做完,所以他希望知道能够完成复习的最短时间。
## 输入格式
本题包含 5 行数据:第 1 行,为四个正整数 s1,s2,s3,s4。
第 2 行,为 A1,A2,....,As1 共 s1 个数,表示第一科习题集每道题目所消耗的时间。
第 3 行,为 B1,B2,....,Bs2 共 s2 个数。
第 4 行,为 C1,C2,....,Cs3 共 s3 个数。
第 5 行,为 D1,D2,....,Ds4 共 s4 个数,意思均同上。
## 输出格式
输出一行,为复习完毕最短时间。
## 样例 #1
### 样例输入 #1
```
1 2 1 3
5
4 3
6
2 4 3
```
### 样例输出 #1
```
20
```
## 提示
1<= s1,s2,s3,s4<= 20。
1<= A1,A2,...,As1,B1,B2,....,Bs2,C1,C2,....,Cs3,D1,D2,....,Ds4<=60。
解题思路
运用dfs对每一种可能进行枚举,枚举每道题交给哪边的脑子解决,找到两边时间较大值的最小值,保存总用时最小的哪一个。
代码
#include
#include
using namespace std;
int g[30];
int d[5];
int sum,max1=99999999; //把记录最小的变量初始化很大
int l,r; //左脑和右脑
int x;
int bj(int x,int y)
{
if(x>y)
return x;
return y;
}
int dfs(int t)
{
if(t>d[x])
{
max1=max1+bj(r,l)-bj(max1,bj(r,l)); //挑出两个脑袋中用时长的一个作为这个科目的总时长
return 0;
}
else
{
r+=g[t];
dfs(t+1); //加在右脑上
r-=g[t];
l+=g[t];
dfs(t+1); //加在左脑上
l-=g[t];
}
return 0;
}
int main()
{
int y;
for(x=1;x<=4;x++)
{
scanf("%d",&d[x]);
}
for(x=1;x<=4;x++)
{
for(y=1;y<=d[x];y++)
{
scanf("%d",&g[y]);
}
dfs(1); //对每一课都进行搜索找出最佳答案
sum+=max1;
r=0;l=0;max1=99999999;
}
printf("%d",sum);
return 0;
} # [COCI 2008/2009 #2] PERKET
## 题目描述
Perket 是一种流行的美食。为了做好 Perket,厨师必须谨慎选择食材,以在保持传统风味的同时尽可能获得最全面的味道。你有 n 种可支配的配料。对于每一种配料,我们知道它们各自的酸度 s 和苦度 b。当我们添加配料时,总的酸度为每一种配料的酸度总乘积;总的苦度为每一种配料的苦度的总和。
众所周知,美食应该做到口感适中,所以我们希望选取配料,以使得酸度和苦度的绝对差最小。
另外,我们必须添加至少一种配料,因为没有任何食物以水为配料的。
## 输入格式
第一行一个整数 n,表示可供选用的食材种类数。
接下来 n 行,每行 2 个整数 si 和 bi,表示第 i 种食材的酸度和苦度。
## 输出格式
一行一个整数,表示可能的总酸度和总苦度的最小绝对差。
## 样例 #1
### 样例输入 #1
```
1
3 10
```
### 样例输出 #1
```
7
```
## 样例 #2
### 样例输入 #2
```
2
3 8
5 8
```
### 样例输出 #2
```
1
```
## 样例 #3
### 样例输入 #3
```
4
1 7
2 6
3 8
4 9
```
### 样例输出 #3
```
1
```
## 提示
#### 数据规模与约定
对于 100% 的数据,有 1 <= n <= 10,且将所有可用食材全部使用产生的总酸度和总苦度小于 1 * 10^9,酸度和苦度不同时为 1 和 0。
解题思路
运用dfs对每一种可能进行枚举,简单题没什么好说的。
代码
#include
#include
using namespace std;
int g[20][3];
int n,min1=99999999,s=1,k=0;
int bj(int x,int y)
{
if(x>y)
return y;
else
return x;
}
int dfs(int x)
{
int y;
if(x>n)
return 0;
else
{
for(y=1;y<=n;y++)
if(g[y][0]==0)
{
g[y][0]=1; //为这种配料打上标记
s*=g[y][1];
k+=g[y][2];
min1=bj(min1,abs(s-k)); //与不加这种配料的酸度和苦度的绝对差进行比较
dfs(x+1);
s/=g[y][1];
k-=g[y][2];
g[y][0]=0;
}
}
return 0;
}
int main()
{
int x;
scanf("%d",&n);
for(x=1;x<=n;x++)
scanf("%d%d",&g[x][1],&g[x][2]);
dfs(1);
printf("%d",min1);
return 0;
}