【小呆的力学笔记】弹塑性力学的初步认知二:应力分析(1)
文章目录
-
-
-
- 1.1 一点的应力状态
- 1.2 一点主应力状态
- 1.3 应力偏张量、球张量、应力不变量
-
-
1.1 一点的应力状态
物体在受到外力或者自身不均匀的温度场等作用时,在其内部会产生内力,物体的内力与方向和截面都有关系。假设有一个受到外力作用的变形体,被一个平面截成A、B两个部分,B部分对A部分施加有作用力,在该截面上的dS微小面积上,作用力为dP,那么我们成dP与dS的比例极限为应力,如下式
σ = lim Δ S → 0 d P d S (1) \boldsymbol\sigma=\lim_{\Delta S\to0} \frac{d\mathbf P}{dS}\tag{1} σ=ΔS→0limdSdP(1)
上式黑体表明是方向相关量。

图 1 内力示意图 图1 内力示意图 图1内力示意图
应力是有方向,我们规定垂直于截面的分量成为正应力,平行于截面的分量为剪应力。
为了分析一点的应力状态,从物体内任一点取一微小的四面体单元,如下图2,其中 σ x x \sigma_{xx} σxx、 σ y y \sigma_{yy} σyy、 σ z z \sigma_{zz} σzz为正应力, τ x y \tau_{xy} τxy、 τ x z \tau_{xz} τxz、 τ y z \tau_{yz} τyz、 τ y x \tau_{yx} τyx、 τ z x \tau_{zx} τzx、 τ z y \tau_{zy} τzy为剪应力,将这些分量放在一起来表示一点的应力状态,组成的应力张量有如下形式,我们不加证明的引出应力张量是二阶张量的这个结论。
[ σ x x σ y x σ z x σ x y σ y y σ z y σ x z σ y z σ z z ] \begin{bmatrix} \sigma_{xx} & \sigma_{yx} & \sigma_{zx}\\ \sigma_{xy} & \sigma_{yy} & \sigma_{zy}\\ \sigma_{xz} & \sigma_{yz} & \sigma_{zz} \end{bmatrix} σxxσxyσxzσyxσyyσyzσzxσzyσzz
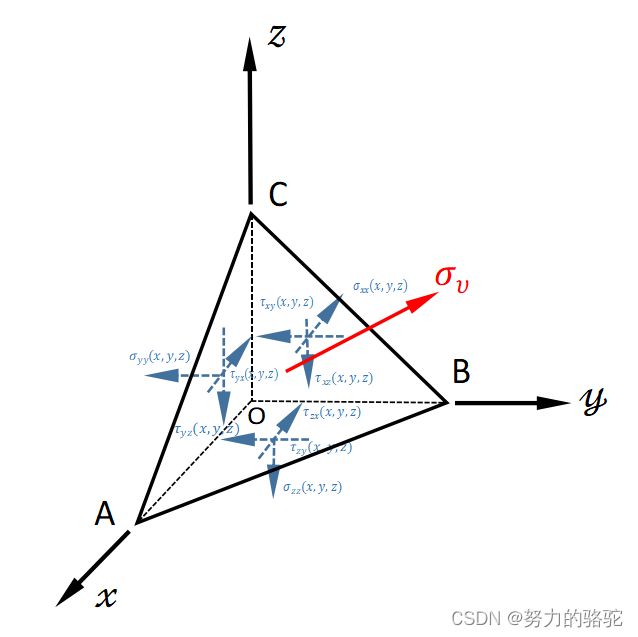
图 2 四面体应力示意图 图2 四面体应力示意图 图2四面体应力示意图
1.2 一点主应力状态
假设该斜面上只有正应力分量,没有剪应力,即图2四面体的斜面上只有正应力 σ v \boldsymbol\sigma_{v} σv,没有剪应力,其中 σ v \boldsymbol\sigma_{v} σv的应力方向余弦为 ( l , m , n ) (l,m,n) (l,m,n),根据力的平衡,可得下式(2)。
σ x x ⋅ S Δ B O C + τ y x ⋅ S Δ A O C + τ z x ⋅ S Δ A O B = σ v x S Δ A B C τ x y ⋅ S Δ B O C + σ y y ⋅ S Δ A O C + τ z y ⋅ S Δ A O B = σ v y S Δ A B C τ x z ⋅ S Δ B O C + τ y z ⋅ S Δ A O C + σ z z ⋅ S Δ A O B = σ v z S Δ A B C (2) \sigma_{xx}\cdot S_{\Delta BOC}+\tau_{yx}\cdot S_{\Delta AOC}+\tau_{zx}\cdot S_{\Delta AOB}=\sigma_{vx}S_{\Delta ABC}\\ \tau_{xy}\cdot S_{\Delta BOC}+\sigma_{yy}\cdot S_{\Delta AOC}+\tau_{zy}\cdot S_{\Delta AOB}=\sigma_{vy}S_{\Delta ABC}\\ \tau_{xz}\cdot S_{\Delta BOC}+\tau_{yz}\cdot S_{\Delta AOC}+\sigma_{zz}\cdot S_{\Delta AOB}=\sigma_{vz}S_{\Delta ABC}\tag{2} σxx⋅SΔBOC+τyx⋅SΔAOC+τzx⋅SΔAOB=σvxSΔABCτxy⋅SΔBOC+σyy⋅SΔAOC+τzy⋅SΔAOB=σvySΔABCτxz⋅SΔBOC+τyz⋅SΔAOC+σzz⋅SΔAOB=σvzSΔABC(2)
其中
S Δ A O C = 1 2 d x d z = S Δ A B C ⋅ m S Δ A O B = 1 2 d x d y = S Δ A B C ⋅ n S Δ B O C = 1 2 d y d z = S Δ A B C ⋅ l (3) S_{\Delta AOC}=\frac{1}{2}dxdz=S_{\Delta ABC}\cdot m\\ S_{\Delta AOB}=\frac{1}{2}dxdy=S_{\Delta ABC}\cdot n\\ S_{\Delta BOC}=\frac{1}{2}dydz=S_{\Delta ABC}\cdot l \tag{3} SΔAOC=21dxdz=SΔABC⋅mSΔAOB=21dxdy=SΔABC⋅nSΔBOC=21dydz=SΔABC⋅l(3)
那么力平衡方程改为
σ x x ⋅ l + τ z x ⋅ n + τ y x ⋅ m = σ v x = σ v l τ x y ⋅ l + σ y y ⋅ m + τ z y ⋅ n = σ v y = σ v m τ x z ⋅ l + τ y z ⋅ m + σ z z ⋅ n = σ v z = σ v n (4) \sigma_{xx}\cdot l+\tau_{zx}\cdot n+\tau_{yx}\cdot m=\sigma_{vx}=\sigma_{v}l\\ \tau_{xy}\cdot l+\sigma_{yy}\cdot m+\tau_{zy}\cdot n=\sigma_{vy}=\sigma_{v}m\\ \tau_{xz}\cdot l+\tau_{yz}\cdot m+\sigma_{zz}\cdot n=\sigma_{vz}=\sigma_{v}n \tag{4} σxx⋅l+τzx⋅n+τyx⋅m=σvx=σvlτxy⋅l+σyy⋅m+τzy⋅n=σvy=σvmτxz⋅l+τyz⋅m+σzz⋅n=σvz=σvn(4)
如果应用张量记法,那么
σ i j n i = p j (5) \sigma_{ij}n_{i} =p_{j} \tag{5} σijni=pj(5)
其中 p j = σ v j p_{j}=\sigma_{vj} pj=σvj
合并同类相,将其改为
( σ x x − σ v ) ⋅ l + τ y x ⋅ m + τ z x ⋅ n = 0 τ x y ⋅ l + ( σ y y − σ v ) ⋅ m + τ z y ⋅ n = 0 τ x z ⋅ l + τ y z ⋅ m + ( σ z z − σ v ) ⋅ n = 0 (6) (\sigma_{xx}-\sigma_{v})\cdot l+\tau_{yx}\cdot m+\tau_{zx}\cdot n=0\\ \tau_{xy}\cdot l+(\sigma_{yy}-\sigma_{v})\cdot m+\tau_{zy}\cdot n=0\\ \tau_{xz}\cdot l+\tau_{yz}\cdot m+(\sigma_{zz}-\sigma_{v})\cdot n=0 \tag{6} (σxx−σv)⋅l+τyx⋅m+τzx⋅n=0τxy⋅l+(σyy−σv)⋅m+τzy⋅n=0τxz⋅l+τyz⋅m+(σzz−σv)⋅n=0(6)
如果应用张量记法,那么
σ i j n i = p j = p n j ⇒ σ i j n i − p n j = σ i j n i − p δ i j n i = ( σ i j − p δ i j ) n i = 0 (7) \sigma_{ij}n_{i} =p_{j}=pn_{j} \Rightarrow \sigma_{ij}n_{i}-pn_{j}=\sigma_{ij}n_{i}-p\delta_{ij} n_{i}=(\sigma_{ij}-p\delta_{ij}) n_{i}=0 \tag{7} σijni=pj=pnj⇒σijni−pnj=σijni−pδijni=(σij−pδij)ni=0(7)
其中 p = σ v = ∣ σ v ∣ p=\sigma_{v}=|\boldsymbol\sigma_{v}| p=σv=∣σv∣
写成矩阵形式,如下式
[ σ x x − σ v τ y x τ z x τ x y σ y y − σ v τ z y τ x z τ y z σ z z − σ v ] [ l m n ] = [ 0 0 0 ] (8) \begin{bmatrix} \sigma_{xx}-\sigma_{v} & \tau_{yx} & \tau_{zx}\\ \tau_{xy} & \sigma_{yy}-\sigma_{v} & \tau_{zy}\\ \tau_{xz} & \tau_{yz} & \sigma_{zz}-\sigma_{v} \end{bmatrix} \begin{bmatrix} l \\m \\n \end{bmatrix}= \begin{bmatrix} 0 \\0 \\0 \end{bmatrix} \tag{8} σxx−σvτxyτxzτyxσyy−σvτyzτzxτzyσzz−σv lmn = 000 (8)
方向余弦存在非零解,那么系数行列式需为零,如下所示。
∣ σ x x − σ v τ y x τ z x τ x y σ y y − σ v τ z y τ x z τ y z σ z z − σ v ∣ = 0 (9) \begin{vmatrix} \sigma_{xx}-\sigma_{v} & \tau_{yx} & \tau_{zx}\\ \tau_{xy} & \sigma_{yy}-\sigma_{v} & \tau_{zy}\\ \tau_{xz} & \tau_{yz} & \sigma_{zz}-\sigma_{v} \end{vmatrix}=0 \tag{9} σxx−σvτxyτxzτyxσyy−σvτyzτzxτzyσzz−σv =0(9)
将其展开,如下式,并利用剪应力互等关系。
∣ σ x x − σ v τ y x τ z x τ x y σ y y − σ v τ z y τ x z τ y z σ z z − σ v ∣ = ( σ x x − σ v ) ( σ y y − σ v ) ( σ z z − σ v ) + τ y x τ z y τ x z + τ z x τ x y τ y z − ( σ y y − σ v ) τ z x τ x z − ( σ z z − σ v ) τ y x τ x y − ( σ x x − σ v ) τ z y τ y z = σ x x σ y y σ z z − ( σ x x σ y y + σ x x σ z z + σ y y σ z z ) σ v + ( σ x x + σ y y + σ z z ) σ v 2 − σ v 3 + 2 τ x z τ x y τ y z + ( τ x z 2 + τ x y 2 + τ y z 2 ) σ v − σ y y τ x z 2 − σ z z τ x y 2 − σ x x τ y z 2 = − σ v 3 + ( σ x x + σ y y + σ z z ) σ v 2 + ( τ x z 2 + τ x y 2 + τ y z 2 − σ x x σ y y − σ x x σ z z − σ y y σ z z ) σ v + σ x x σ y y σ z z + 2 τ x z τ x y τ y z − σ y y τ x z 2 − σ z z τ x y 2 − σ x x τ y z 2 = − σ v 3 + I 1 σ v 2 + I 2 σ v + I 3 = 0 (10) \begin{aligned} \begin{vmatrix} \sigma_{xx}-\sigma_{v} & \tau_{yx} & \tau_{zx}\\ \tau_{xy} & \sigma_{yy}-\sigma_{v} & \tau_{zy}\\ \tau_{xz} & \tau_{yz} & \sigma_{zz}-\sigma_{v} \end{vmatrix}=&(\sigma_{xx}-\sigma_{v})(\sigma_{yy}-\sigma_{v})(\sigma_{zz}-\sigma_{v})+\tau_{yx}\tau_{zy}\tau_{xz}+\tau_{zx}\tau_{xy}\tau_{yz}\\ &-(\sigma_{yy}-\sigma_{v})\tau_{zx}\tau_{xz}-(\sigma_{zz}-\sigma_{v})\tau_{yx}\tau_{xy}-(\sigma_{xx}-\sigma_{v})\tau_{zy}\tau_{yz}\\ =&\sigma_{xx}\sigma_{yy}\sigma_{zz}-(\sigma_{xx}\sigma_{yy}+\sigma_{xx}\sigma_{zz}+\sigma_{yy}\sigma_{zz})\sigma_{v}+(\sigma_{xx}+\sigma_{yy}+\sigma_{zz})\sigma_{v}^2\\ &-\sigma_{v}^3+2\tau_{xz}\tau_{xy}\tau_{yz}+(\tau_{xz}^2+\tau_{xy}^2+\tau_{yz}^2)\sigma_{v}-\sigma_{yy}\tau_{xz}^2-\sigma_{zz}\tau_{xy}^2-\sigma_{xx}\tau_{yz}^2\\ =&-\sigma_{v}^3+(\sigma_{xx}+\sigma_{yy}+\sigma_{zz})\sigma_{v}^2+\\ &(\tau_{xz}^2+\tau_{xy}^2+\tau_{yz}^2-\sigma_{xx}\sigma_{yy}-\sigma_{xx}\sigma_{zz}-\sigma_{yy}\sigma_{zz})\sigma_{v}+\\ &\sigma_{xx}\sigma_{yy}\sigma_{zz}+2\tau_{xz}\tau_{xy}\tau_{yz}-\sigma_{yy}\tau_{xz}^2-\sigma_{zz}\tau_{xy}^2-\sigma_{xx}\tau_{yz}^2\\ =&-\sigma_{v}^3+I_1\sigma_{v}^2+I_2\sigma_{v}+I_3=0 \end{aligned}\tag{10} σxx−σvτxyτxzτyxσyy−σvτyzτzxτzyσzz−σv ====(σxx−σv)(σyy−σv)(σzz−σv)+τyxτzyτxz+τzxτxyτyz−(σyy−σv)τzxτxz−(σzz−σv)τyxτxy−(σxx−σv)τzyτyzσxxσyyσzz−(σxxσyy+σxxσzz+σyyσzz)σv+(σxx+σyy+σzz)σv2−σv3+2τxzτxyτyz+(τxz2+τxy2+τyz2)σv−σyyτxz2−σzzτxy2−σxxτyz2−σv3+(σxx+σyy+σzz)σv2+(τxz2+τxy2+τyz2−σxxσyy−σxxσzz−σyyσzz)σv+σxxσyyσzz+2τxzτxyτyz−σyyτxz2−σzzτxy2−σxxτyz2−σv3+I1σv2+I2σv+I3=0(10)
其中 I 1 I_1 I1、 I 2 I_2 I2、 I 3 I_3 I3成为应力不变量,如下所示。
I 1 = σ x x + σ y y + σ z z = t r [ σ ] I 2 = τ x z 2 + τ x y 2 + τ y z 2 − σ x x σ y y − σ x x σ z z − σ y y σ z z I 3 = σ x x σ y y σ z z + 2 τ x z τ x y τ y z − σ y y τ x z 2 − σ z z τ x y 2 − σ x x τ y z 2 = ∣ σ ∣ (11) \begin{aligned} I_1&=\sigma_{xx}+\sigma_{yy}+\sigma_{zz}=tr[\boldsymbol \sigma]\\ I_2&=\tau_{xz}^2+\tau_{xy}^2+\tau_{yz}^2-\sigma_{xx}\sigma_{yy}-\sigma_{xx}\sigma_{zz}-\sigma_{yy}\sigma_{zz}\\ I_3&=\sigma_{xx}\sigma_{yy}\sigma_{zz}+2\tau_{xz}\tau_{xy}\tau_{yz}-\sigma_{yy}\tau_{xz}^2-\sigma_{zz}\tau_{xy}^2-\sigma_{xx}\tau_{yz}^2=|\boldsymbol \sigma| \end{aligned}\tag{11} I1I2I3=σxx+σyy+σzz=tr[σ]=τxz2+τxy2+τyz2−σxxσyy−σxxσzz−σyyσzz=σxxσyyσzz+2τxzτxyτyz−σyyτxz2−σzzτxy2−σxxτyz2=∣σ∣(11)
如果应用张量记法,那么
I 1 = σ i i (12) I_1=\sigma_{ii}\tag{12} I1=σii(12)
I 2 = τ x z 2 + τ x y 2 + τ y z 2 − σ x x σ y y − σ x x σ z z − σ y y σ z z = τ x z 2 + τ x y 2 + τ y z 2 + 1 2 ( σ x x 2 + σ y y 2 + σ z z 2 ) − 1 2 ( σ x x 2 + σ y y 2 + σ z z 2 ) − σ x x σ y y − σ x x σ z z − σ y y σ z z = 1 2 σ i j σ i j − 1 2 σ i i σ j j = − 1 2 ( σ i i σ j j − σ i j σ i j ) (13) \begin{aligned} I_2&=\tau_{xz}^2+\tau_{xy}^2+\tau_{yz}^2-\sigma_{xx}\sigma_{yy}-\sigma_{xx}\sigma_{zz}-\sigma_{yy}\sigma_{zz}\\ &=\tau_{xz}^2+\tau_{xy}^2+\tau_{yz}^2 + \frac{1}{2}(\sigma_{xx}^2+ \sigma_{yy}^2+ \sigma_{zz}^2)-\frac{1}{2}(\sigma_{xx}^2+ \sigma_{yy}^2+ \sigma_{zz}^2)-\sigma_{xx}\sigma_{yy}-\sigma_{xx}\sigma_{zz}-\sigma_{yy}\sigma_{zz}\\ &=\frac{1}{2}\sigma_{ij}\sigma_{ij}-\frac{1}{2}\sigma_{ii}\sigma_{jj}\\ &=-\frac{1}{2}(\sigma_{ii}\sigma_{jj}-\sigma_{ij}\sigma_{ij}) \end{aligned}\tag{13} I2=τxz2+τxy2+τyz2−σxxσyy−σxxσzz−σyyσzz=τxz2+τxy2+τyz2+21(σxx2+σyy2+σzz2)−21(σxx2+σyy2+σzz2)−σxxσyy−σxxσzz−σyyσzz=21σijσij−21σiiσjj=−21(σiiσjj−σijσij)(13)
那么,观察公式(9)不难法线 σ v \sigma_{v} σv就是系数矩阵的特征值,而方向余弦向量就是特征向量。
1.3 应力偏张量、球张量、应力不变量
下图3为能反映一点的应力状态的六面体,众多的金属实验表明(在常见的应力范围内)当六面体各个面上只有相等正应力无切应力时,物体不发生塑性变形和形状变化。由此,定义了这么一种应力状态,即只有主应力并且主应力相等,如下式,称应力球张量。
[ σ m ] = [ σ m 0 0 0 σ m 0 0 0 σ m ] (14) [\boldsymbol\sigma_m]=\begin{bmatrix} \sigma_{m} & 0 & 0\\ 0 & \sigma_{m} & 0\\ 0 & 0 & \sigma_{m} \end{bmatrix}\tag{14} [σm]= σm000σm000σm (14)
那么 σ m = 1 3 I 1 = 1 3 ( σ x x + σ y y + σ z z ) (15) \sigma_m=\frac{1}{3}I_1=\frac{1}{3}(\sigma_{xx}+\sigma_{yy}+\sigma_{zz})\tag{15} σm=31I1=31(σxx+σyy+σzz)(15)

图 3 六面体应力示意图 图3 六面体应力示意图 图3六面体应力示意图
那么将应力张量减去应力球张量,可得应力偏张量(同时可以确定的是[s]也是对称矩阵)
[ s ] = [ σ x x − σ m τ x y τ x z τ y x σ y y − σ m τ y z τ z x τ z y σ z z − σ m ] = [ s x x s x y s x z s y x s y y s y z s z x s z y s z z ] (16) [\boldsymbol s]=\begin{bmatrix} \sigma_{xx}-\sigma_{m} & \tau_{xy} & \tau_{xz}\\ \tau_{yx} & \sigma_{yy}-\sigma_{m} & \tau_{yz}\\ \tau_{zx} & \tau_{zy} & \sigma_{zz}-\sigma_{m} \end{bmatrix} =\begin{bmatrix} s_{xx} & s_{xy} & s_{xz}\\ s_{yx} & s_{yy} & s_{yz}\\ s_{zx} & s_{zy} & s_{zz} \end{bmatrix}\tag{16} [s]= σxx−σmτyxτzxτxyσyy−σmτzyτxzτyzσzz−σm = sxxsyxszxsxysyyszysxzsyzszz (16)
同样,按照第2节的推导过程,可以得到应力偏张量的特征方程的公式如下所示。
∣ s x x − s v s y x s z x s x y s y y − s v s z y s x z s y z s z z − s v ∣ = ∣ s x x − s v s x y s x z s y x s y y − s v s y z s z x s z y s z z − s v ∣ = − s v 3 + I ^ 1 s v 2 + I ^ 2 s v + I ^ 3 = 0 (17) \begin{aligned} \begin{vmatrix} s_{xx}-s_{v} & s_{yx} & s_{zx}\\ s_{xy} & s_{yy}-s_{v} & s_{zy}\\ s_{xz} & s_{yz} & s_{zz}-s_{v} \end{vmatrix}&=\begin{vmatrix} s_{xx}-s_{v} & s_{xy} & s_{xz}\\ s_{yx} & s_{yy}-s_{v} & s_{yz}\\ s_{zx} & s_{zy} & s_{zz}-s_{v} \end{vmatrix}\\ &=-s_{v}^3+\hat I_1s_{v}^2+\hat I_2s_{v}+\hat I_3=0 \end{aligned}\tag{17} sxx−svsxysxzsyxsyy−svsyzszxszyszz−sv = sxx−svsyxszxsxysyy−svszysxzsyzszz−sv =−sv3+I^1sv2+I^2sv+I^3=0(17)
其中,有应力偏张量的不变量如下所示。
I ^ 1 = s x x + s y y + s z z = σ x x − σ m + σ y y − σ m + σ z z − σ m = 0 I ^ 2 = s x z 2 + s x y 2 + s y z 2 − s x x s y y − s x x s z z − s y y s z z I ^ 3 = s x x s y y s z z + 2 s x z s x y s y z − s y y s x z 2 − s z z s x y 2 − s x x s y z 2 (18) \begin{aligned}\hat I_1&=s_{xx}+s_{yy}+s_{zz}=\sigma_{xx}-\sigma_{m} + \sigma_{yy}-\sigma_{m}+ \sigma_{zz}-\sigma_{m}=0\\ \hat I_2&=s_{xz}^2+s_{xy}^2+s_{yz}^2-s_{xx}s_{yy}-s_{xx}s_{zz}-s_{yy}s_{zz}\\ \hat I_3&=s_{xx}s_{yy}s_{zz}+2s_{xz}s_{xy}s_{yz}-s_{yy}s_{xz}^2-s_{zz}s_{xy}^2-s_{xx}s_{yz}^2 \end{aligned}\tag{18} I^1I^2I^3=sxx+syy+szz=σxx−σm+σyy−σm+σzz−σm=0=sxz2+sxy2+syz2−sxxsyy−sxxszz−syyszz=sxxsyyszz+2sxzsxysyz−syysxz2−szzsxy2−sxxsyz2(18)
对公式(15)进行展开合并同类项等过程,如下所示,
− s v 3 + I ^ 1 s v 2 + I ^ 2 s v + I ^ 3 = − s v 3 + I ^ 2 s v + I ^ 3 = − s v 3 + ( s x z 2 + s x y 2 + s y z 2 − s x x s y y − s x x s z z − s y y s z z ) s v + s x x s y y s z z + 2 s x z s x y s y z − s y y s x z 2 − s z z s x y 2 − s x x s y z 2 = − s v 3 + ( τ x z 2 + τ x y 2 + τ y z 2 ) s v − [ ( σ x x − σ m ) ( σ y y − σ m ) + ( σ x x − σ m ) ( σ z z − σ m ) + ( σ y y − σ m ) ( σ z z − σ m ) ] s v + ( σ x x − σ m ) ( σ y y − σ m ) ( σ z z − σ m ) + 2 τ x z τ x y τ y z − ( σ y y − σ m ) τ x z 2 − ( σ z z − σ m ) τ x y 2 − ( σ x x − σ m ) τ y z 2 = − s v 3 + ( τ x z 2 + τ x y 2 + τ y z 2 ) s v − ( σ x x σ y y + σ x x σ z z + σ y y σ z z ) s v + ( σ x x + σ y y + σ x x + σ z z + σ y y + σ z z ) σ m s v − 3 σ m 2 s v + σ x x σ y y σ z z − ( σ x x σ y y + σ x x σ z z + σ y y σ z z ) σ m + ( σ x x + σ y y + σ z z ) σ m 2 − σ m 3 + 2 τ x z τ x y τ y z − ( σ y y τ x z 2 + σ z z τ x y 2 + σ x x τ y z 2 ) + ( τ x z 2 + τ x y 2 + τ y z 2 ) σ m = − s v 3 + ( τ x z 2 + τ x y 2 + τ y z 2 ) ( s v + σ m ) − ( σ x x σ y y + σ x x σ z z + σ y y σ z z ) ( s v + σ m ) + 6 σ m 2 s v − 3 σ m 2 s v + σ x x σ y y σ z z + 3 σ m 3 − σ m 3 + 2 τ x z τ x y τ y z − ( σ y y τ x z 2 + σ z z τ x y 2 + σ x x τ y z 2 ) = − s v 3 + 3 σ m 2 s v + 2 σ m 3 + ( τ x z 2 + τ x y 2 + τ y z 2 − σ x x σ y y − σ x x σ z z − σ y y σ z z ) ( s v + σ m ) + σ x x σ y y σ z z + 2 τ x z τ x y τ y z − ( σ y y τ x z 2 + σ z z τ x y 2 + σ x x τ y z 2 ) = − s v 3 − σ m 3 + 3 σ m 2 s v + 3 σ m 3 + I 2 ( s v + σ m ) + I 3 = − ( s v + σ m ) ( s v 2 − s v σ m + σ m 2 − 3 σ m 2 ) + I 2 ( s v + σ m ) + I 3 = − ( s v + σ m ) ( s v + σ m ) ( s v − 2 σ m ) + I 2 ( s v + σ m ) + I 3 = − ( s v + σ m ) 2 ( s v + σ m − 3 σ m ) + I 2 ( s v + σ m ) + I 3 = − ( s v + σ m ) 3 + 3 σ m ( s v + σ m ) 2 + I 2 ( s v + σ m ) + I 3 = − ( s v + σ m ) 3 + I 1 ( s v + σ m ) 2 + I 2 ( s v + σ m ) + I 3 = 0 (19) \begin{aligned} -s_{v}^3+\hat I_1s_{v}^2+\hat I_2s_{v}+\hat I_3&=-s_{v}^3+\hat I_2s_{v}+\hat I_3\\ &=-s_{v}^3+(s_{xz}^2+s_{xy}^2+s_{yz}^2-s_{xx}s_{yy}-s_{xx}s_{zz}-s_{yy}s_{zz})s_{v}\\ &\quad+s_{xx}s_{yy}s_{zz}+2s_{xz}s_{xy}s_{yz}-s_{yy}s_{xz}^2-s_{zz}s_{xy}^2-s_{xx}s_{yz}^2\\ &=-s_{v}^3+(\tau_{xz}^2+\tau_{xy}^2+\tau_{yz}^2)s_{v} \\ &\quad- [(\sigma_{xx}-\sigma_{m})(\sigma_{yy}-\sigma_{m})+(\sigma_{xx}-\sigma_{m})(\sigma_{zz}-\sigma_{m})+(\sigma_{yy}-\sigma_{m})( \sigma_{zz}-\sigma_{m})]s_{v}\\ &\quad+(\sigma_{xx}-\sigma_{m})(\sigma_{yy}-\sigma_{m})(\sigma_{zz}-\sigma_{m})+2\tau_{xz}\tau_{xy}\tau_{yz}\\ &\quad-(\sigma_{yy}-\sigma_{m})\tau_{xz}^2-(\sigma_{zz}-\sigma_{m})\tau_{xy}^2-(\sigma_{xx}-\sigma_{m})\tau_{yz}^2\\ &=-s_{v}^3+(\tau_{xz}^2+\tau_{xy}^2+\tau_{yz}^2)s_{v}-(\sigma_{xx}\sigma_{yy}+\sigma_{xx}\sigma_{zz}+\sigma_{yy}\sigma_{zz})s_{v}\\ &\quad+(\sigma_{xx}+\sigma_{yy}+\sigma_{xx}+\sigma_{zz}+\sigma_{yy}+\sigma_{zz})\sigma_{m}s_{v}-3\sigma_{m}^2s_{v}+\sigma_{xx}\sigma_{yy}\sigma_{zz}\\ &\quad-(\sigma_{xx}\sigma_{yy}+\sigma_{xx}\sigma_{zz}+\sigma_{yy}\sigma_{zz})\sigma_{m}+(\sigma_{xx}+\sigma_{yy}+\sigma_{zz})\sigma_{m}^2-\sigma_{m}^3+2\tau_{xz}\tau_{xy}\tau_{yz}\\ &\quad-(\sigma_{yy}\tau_{xz}^2+\sigma_{zz}\tau_{xy}^2+\sigma_{xx}\tau_{yz}^2)+(\tau_{xz}^2+\tau_{xy}^2+\tau_{yz}^2)\sigma_{m}\\ &=-s_{v}^3+(\tau_{xz}^2+\tau_{xy}^2+\tau_{yz}^2)(s_{v}+\sigma_{m})-(\sigma_{xx}\sigma_{yy}+\sigma_{xx}\sigma_{zz}+\sigma_{yy}\sigma_{zz})(s_{v}+\sigma_{m})\\ &\quad+6\sigma_{m}^2s_{v}-3\sigma_{m}^2s_{v}+\sigma_{xx}\sigma_{yy}\sigma_{zz}+3\sigma_{m}^3-\sigma_{m}^3+2\tau_{xz}\tau_{xy}\tau_{yz}\\ &\quad-(\sigma_{yy}\tau_{xz}^2+\sigma_{zz}\tau_{xy}^2+\sigma_{xx}\tau_{yz}^2)\\ &=-s_{v}^3+3\sigma_{m}^2s_{v}+2\sigma_{m}^3+(\tau_{xz}^2+\tau_{xy}^2+\tau_{yz}^2-\sigma_{xx}\sigma_{yy}-\sigma_{xx}\sigma_{zz}-\sigma_{yy}\sigma_{zz})(s_{v}+\sigma_{m})\\ &\quad+\sigma_{xx}\sigma_{yy}\sigma_{zz}+2\tau_{xz}\tau_{xy}\tau_{yz}-(\sigma_{yy}\tau_{xz}^2+\sigma_{zz}\tau_{xy}^2+\sigma_{xx}\tau_{yz}^2)\\ &=-s_{v}^3-\sigma_{m}^3+3\sigma_{m}^2s_{v}+3\sigma_{m}^3+I_2(s_{v}+\sigma_{m})+I_3\\ &=-(s_{v}+\sigma_{m})(s_{v}^2-s_{v}\sigma_{m}+\sigma_{m}^2-3\sigma_{m}^2)+I_2(s_{v}+\sigma_{m})+I_3\\ &=-(s_{v}+\sigma_{m})(s_{v}+\sigma_{m})(s_{v}-2\sigma_{m})+I_2(s_{v}+\sigma_{m})+I_3\\ &=-(s_{v}+\sigma_{m})^2(s_{v}+\sigma_{m}-3\sigma_{m})+I_2(s_{v}+\sigma_{m})+I_3\\ &=-(s_{v}+\sigma_{m})^3+3\sigma_{m}(s_{v}+\sigma_{m})^2+I_2(s_{v}+\sigma_{m})+I_3\\ &=-(s_{v}+\sigma_{m})^3+I_1(s_{v}+\sigma_{m})^2+I_2(s_{v}+\sigma_{m})+I_3=0 \end{aligned}\tag{19} −sv3+I^1sv2+I^2sv+I^3=−sv3+I^2sv+I^3=−sv3+(sxz2+sxy2+syz2−sxxsyy−sxxszz−syyszz)sv+sxxsyyszz+2sxzsxysyz−syysxz2−szzsxy2−sxxsyz2=−sv3+(τxz2+τxy2+τyz2)sv−[(σxx−σm)(σyy−σm)+(σxx−σm)(σzz−σm)+(σyy−σm)(σzz−σm)]sv+(σxx−σm)(σyy−σm)(σzz−σm)+2τxzτxyτyz−(σyy−σm)τxz2−(σzz−σm)τxy2−(σxx−σm)τyz2=−sv3+(τxz2+τxy2+τyz2)sv−(σxxσyy+σxxσzz+σyyσzz)sv+(σxx+σyy+σxx+σzz+σyy+σzz)σmsv−3σm2sv+σxxσyyσzz−(σxxσyy+σxxσzz+σyyσzz)σm+(σxx+σyy+σzz)σm2−σm3+2τxzτxyτyz−(σyyτxz2+σzzτxy2+σxxτyz2)+(τxz2+τxy2+τyz2)σm=−sv3+(τxz2+τxy2+τyz2)(sv+σm)−(σxxσyy+σxxσzz+σyyσzz)(sv+σm)+6σm2sv−3σm2sv+σxxσyyσzz+3σm3−σm3+2τxzτxyτyz−(σyyτxz2+σzzτxy2+σxxτyz2)=−sv3+3σm2sv+2σm3+(τxz2+τxy2+τyz2−σxxσyy−σxxσzz−σyyσzz)(sv+σm)+σxxσyyσzz+2τxzτxyτyz−(σyyτxz2+σzzτxy2+σxxτyz2)=−sv3−σm3+3σm2sv+3σm3+I2(sv+σm)+I3=−(sv+σm)(sv2−svσm+σm2−3σm2)+I2(sv+σm)+I3=−(sv+σm)(sv+σm)(sv−2σm)+I2(sv+σm)+I3=−(sv+σm)2(sv+σm−3σm)+I2(sv+σm)+I3=−(sv+σm)3+3σm(sv+σm)2+I2(sv+σm)+I3=−(sv+σm)3+I1(sv+σm)2+I2(sv+σm)+I3=0(19)
对比公式(19)和公式(10),如下所示。
− ( s v + σ m ) 3 + I 1 ( s v + σ m ) 2 + I 2 ( s v + σ m ) + I 3 = 0 − σ v 3 + I 1 σ v 2 + I 2 σ v + I 3 = 0 -(s_{v}+\sigma_{m})^3+I_1(s_{v}+\sigma_{m})^2+I_2(s_{v}+\sigma_{m})+I_3=0\\ -\sigma_{v}^3+I_1\sigma_{v}^2+I_2\sigma_{v}+I_3=0 −(sv+σm)3+I1(sv+σm)2+I2(sv+σm)+I3=0−σv3+I1σv2+I2σv+I3=0
不难发现, s v + σ m = σ v s_{v}+\sigma_{m}=\sigma_{v} sv+σm=σv,即应力偏张量主值和应力张量主值存在以上转换关系。
同时,从公式(18)的 I ^ 1 \hat I_1 I^1
I ^ 1 = s x x + s y y + s z z = 0 \hat I_1=s_{xx}+s_{yy}+s_{zz}=0 I^1=sxx+syy+szz=0
那么可以得到
( s x x + s y y + s z z ) 2 = s x x 2 + s y y 2 + s z z 2 + 2 ( s x x s y y + s x x s z z + s y y s z z ) = 0 (20) (s_{xx}+s_{yy}+s_{zz})^2=s_{xx}^2+s_{yy}^2+s_{zz}^2+2(s_{xx}s_{yy}+s_{xx}s_{zz}+s_{yy}s_{zz})=0\tag{20} (sxx+syy+szz)2=sxx2+syy2+szz2+2(sxxsyy+sxxszz+syyszz)=0(20)
于是
− 6 ( s x x s y y + s x x s z z + s y y s z z ) = 2 s x x 2 + 2 s y y 2 + 2 s z z 2 − 2 ( s x x s y y + s x x s z z + s y y s z z ) = ( s x x − s y y ) 2 + ( s x x − s z z ) 2 + ( s y y − s z z ) 2 = ( σ x x − σ y y ) 2 + ( σ x x − σ z z ) 2 + ( σ y y − σ z z ) 2 (21) \begin{aligned} -6(s_{xx}s_{yy}+s_{xx}s_{zz}+s_{yy}s_{zz})&=2s_{xx}^2+2s_{yy}^2+2s_{zz}^2-2(s_{xx}s_{yy}+s_{xx}s_{zz}+s_{yy}s_{zz})\\ &=(s_{xx}-s_{yy})^2+(s_{xx}-s_{zz})^2+(s_{yy}-s_{zz})^2\\ &=(\sigma_{xx}-\sigma_{yy})^2+(\sigma_{xx}-\sigma_{zz})^2+(\sigma_{yy}-\sigma_{zz})^2 \end{aligned}\tag{21} −6(sxxsyy+sxxszz+syyszz)=2sxx2+2syy2+2szz2−2(sxxsyy+sxxszz+syyszz)=(sxx−syy)2+(sxx−szz)2+(syy−szz)2=(σxx−σyy)2+(σxx−σzz)2+(σyy−σzz)2(21)
将公式(18)的 I ^ 2 \hat I_2 I^2代入,那么
− 6 ( s x x s y y + s x x s z z + s y y s z z ) = 6 [ I ^ 2 − ( τ x z 2 + τ x y 2 + τ y z 2 ) ] = ( σ x x − σ y y ) 2 + ( σ x x − σ z z ) 2 + ( σ y y − σ z z ) 2 (22) \begin{aligned} -6(s_{xx}s_{yy}+s_{xx}s_{zz}+s_{yy}s_{zz})&=6[\hat I_2-(\tau_{xz}^2+\tau_{xy}^2+\tau_{yz}^2)]\\ &=(\sigma_{xx}-\sigma_{yy})^2+(\sigma_{xx}-\sigma_{zz})^2+(\sigma_{yy}-\sigma_{zz})^2 \end{aligned}\tag{22} −6(sxxsyy+sxxszz+syyszz)=6[I^2−(τxz2+τxy2+τyz2)]=(σxx−σyy)2+(σxx−σzz)2+(σyy−σzz)2(22)
I ^ 2 = 1 6 [ ( σ x x − σ y y ) 2 + ( σ x x − σ z z ) 2 + ( σ y y − σ z z ) 2 + 6 ( τ x z 2 + τ x y 2 + τ y z 2 ) ] (23) \hat I_2=\frac{1}{6}[(\sigma_{xx}-\sigma_{yy})^2+(\sigma_{xx}-\sigma_{zz})^2+(\sigma_{yy}-\sigma_{zz})^2+6(\tau_{xz}^2+\tau_{xy}^2+\tau_{yz}^2)]\tag{23} I^2=61[(σxx−σyy)2+(σxx−σzz)2+(σyy−σzz)2+6(τxz2+τxy2+τyz2)](23)
应力偏张量的第二不变量更常用的还有一个形式如下。
I ^ 2 = 1 6 [ ( σ 1 − σ 2 ) 2 + ( σ 1 − σ 3 ) 2 + ( σ 2 − σ 3 ) 2 ] (24) \hat I_2=\frac{1}{6}[(\sigma_{1}-\sigma_{2})^2+(\sigma_{1}-\sigma_{3})^2+(\sigma_{2}-\sigma_{3})^2]\tag{24} I^2=61[(σ1−σ2)2+(σ1−σ3)2+(σ2−σ3)2](24)
看公式(23)(24)是不是特别的眼熟,其实他就是等效应力的来源,后面还会经常用到。