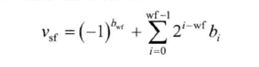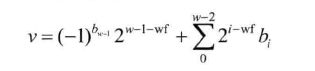一文看懂定点数和浮点数
在计算机科学和工程领域,数字表示法至关重要,涉及到数据的存储、计算和处理。主要有两种数字表示法:定点数和浮点数。
定点数的小数点位置固定,适用于二进制计数系统和数字信号处理等。其优点在于表示简单,但大数值时精度低,易溢出。
浮点数的小数点位置不固定,能自动调整,适用于浮点运算和科学计算等。其优点在于表示范围广、精度高,但数值溢出不易察觉,运算规则复杂。
实际应用中,根据需求选择合适的数字表示法。如高精度和复杂运算场景适合浮点数,而对精度要求不高的场景如二进制计数和数字信号处理则可选用定点数。此外,两者间可相互转换,实现灵活运用。本文将详细介绍两种数字表示
浮点数
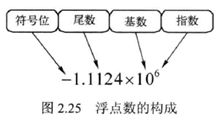
1、构成:
符号位、尾数、基数、指数
2、浮点数二进制表示
基数为2,只保留符号位(s)、尾数(m)、指数(e):
3、浮点数格式:
单精度、双精度和扩展精度。
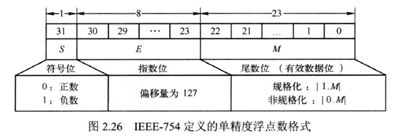
单精度浮点数为32位:
对应于C语言中的float,其中包含一位符号位S,8位指数位E和23位尾数位M,尽管M有23位,但他表示小数点之后的二进制小数,例如M为0110,其实是0.0110,这时因为标准规定小数点左边还有一个隐含位.(此处有一个点.),从而尾数值可能是0.0110,也可能是1.0110。E关系到规格化和非规格化。
双精度浮点数为64位:
对应于C语言中的double。
4、规格化
当指数位E表示的二进制序列不全0也不全1时,该浮点数为规格化形式。此时,指数位对应的实际值e被解释为表示偏置(bias)形式的整数,相应的计算公式为:
| E |表示E的二进制序列表示的整数值;bias为偏移量;k为指数位宽度,对于单精度而言,k=8,故bias=127,E=10000001(binary)时,| E |=129(decimal),所以e=129-127=2。
对于规格化浮点数,IEEE—754标准规定尾数位小数点左侧的隐含位位1,此时m的计算公式为:
m=| 1.M |
M=“1001000….0”,1.M=1.1001000…0,带入上式得到 m=1+2^(-1)+2^(-4)=1.5625。
所以:
n=(-1)^(0) x (1.5625)^(2)= 2.44140625
5、单精度规格化浮点数特点
(1)、由于E表示的二进制序列几部全为0也不全为1,所以E的表示范围为0~255.
(2)、尾数m的最小值为1,对应的M全为0,最大值为2-2^(-23)
(3)、规格化浮点数能表示的数绝对值最大值为(2-2^(-23))x 2^(127)。
单精度规格化浮点数计算公式为:
6、非规格化
当E的二进制位全部为0时,该浮点数为非规格化形式。指数位e和m为:
单精度非规格化浮点数计算公式为:
定点数
1、定点数定义
定点数是指小数点固定的隐含在某一位置上的一类数据
有符号数:
以四位有符号数1111为例,其数值大小为:1x(-2^(0))(4+2+1)= -7。
2、补码
正整数的补码:与原码相同。
负整数的补码:将其原码除符号位外的所有位取反,之后加1。
3、定点纯小数
定点纯小数是指整数部分为0的定点小数,分为有符号定点纯小数和无符号定点纯小数,S为符号位,小数点在小数位的最左侧。
对于字长为wf的无符号定点小数,其数值可表示为:
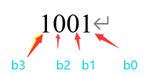
Bi表示对应的位为1,以四位无符号定点纯小数1001为例:
其值为value=b0 x 2^(0-4) +b3 x 2^(3-4) =0.0625+0.5=0.5625
对于字长为wf+1的有符号定点纯小数,其数值表示为:
同样以1001为例,字长为4,wf=3,符号位为1,尾数位001,其值表示为:
value= (-1)^(1) + 2^(0-3) =-1+0.125 = -0.875
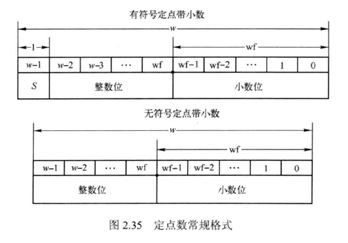
4、定点带小数
即整数部分不为0的小数,分为有符号定点带小数额无符号定点带小数,S为符号位,定点数位宽为w,小数位位宽为wf:
对于无符号定点带小数,正常计算即可,其计算公式为:
对于有符号定点带小数,其计算公式为:
5、定点数据的上溢和下溢
上溢(overflow):运算结果超出了定点数的整数部分所能表示的范围,
下溢(underflow):运算结果小数部分超出了小数部分能表示的范围。
UFIX_4_2,表示无符号型定点小数,全长为4,小数部分宽度为2,所能表示的范围为:[0,3.75],精度为0.25,如果运算结果为4,即发生上溢,如果运算结果为0.125,则发生下溢。
6、浮点数和定点数的比较
与定点数相比,采用浮点数进行算法描述:
(1)、具有更宽的动态范围。
(2)、可缩短复杂运算的开发周期。
(3)、统一的标准数据格式。
劣势:
(1)、浮点运算会消耗更多的查找表、寄存器和乘法器。
(2)、浮点运算会给布线资源带来压力,导致最大运行频率降低。
通常在算法建模时采用浮点数,而在FPGA实现时采用定点数。