Serialize and Deserialize Binary Tree

Problem

Serialization is the process of converting a data structure or object into a sequence of bits so that it can be stored in a file or memory buffer, or transmitted across a network connection link to be reconstructed later in the same or another computer environment.

Design an algorithm to serialize and deserialize a binary tree. There is no restriction on how your serialization/deserialization algorithm should work. You just need to ensure that a binary tree can be serialized to a string and this string can be deserialized to the original tree structure.

Clarification: The input/output format is the same as how LeetCode serializes a binary tree. You do not necessarily need to follow this format, so please be creative and come up with different approaches yourself.

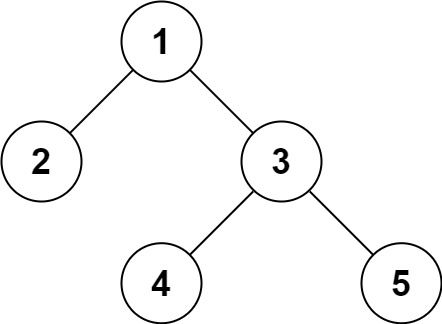
Example 1:

Input: root = [1,2,3,null,null,4,5]
Output: [1,2,3,null,null,4,5]

Example 2:

Input: root = []
Output: []

Intuition

The task is to design an algorithm for serializing and deserializing a binary tree. Serialization is the process of converting a data structure into a sequence of bits or characters, and deserialization is the reverse process. In the case of a binary tree, we need to find a way to represent the tree structure in a string format and reconstruct the original tree from the string.

Approach

Serialization:

Implement a recursive DFS (Depth-First Search) function dfs_serialize to traverse the tree and append the values of nodes to a list (res). If a node is None, append the character 'N' to represent a null node.
Join the list of values into a string using a delimiter (e.g., ',') and return the serialized string.
Deserialization:

Split the serialized string into a list of values using the delimiter.
Implement a recursive DFS function dfs_deserialize to construct the binary tree from the list of values. If the current value is 'N', return None to represent a null node. Otherwise, create a new TreeNode with the integer value and recursively set its left and right children.
Return Result:

In the serialize method, return the serialized string.
In the deserialize method, return the root of the reconstructed binary tree.

Complexity

• Time complexity:

Serialization: The time complexity of serialization is O(n), where n is the number of nodes in the binary tree. Each node is visited exactly once during the recursive traversal.
Deserialization: The time complexity of deserialization is O(n), where n is the number of nodes in the binary tree. Each value in the list is processed exactly once.

• Space complexity:

Serialization: The space complexity of serialization is O(h), where h is the height of the binary tree. This is because the maximum depth of the recursion stack is equal to the height of the tree. In the average case, for a balanced binary tree, the height is O(log n). However, in the worst case of an unbalanced tree, the height could be O(n).
Deserialization: The space complexity of deserialization is O(h), where h is the height of the binary tree. This is due to the recursive call stack during the deserialization process. In the average case, for a balanced binary tree, the height is O(log n). However, in the worst case of an unbalanced tree, the height could be O(n). The space complexity is dominated by the depth of the recursive call stack.

Code

# Definition for a binary tree node.
# class TreeNode(object):
#     def __init__(self, x):
#         self.val = x
#         self.left = None
#         self.right = None

class Codec:

    def serialize(self, root):
        res = []

        def dfs(node):
            if not node:
                res.append('N')
                return 
            
            res.append(str(node.val))
            dfs(node.left)
            dfs(node.right)
        
        dfs(root)
        return ','.join(res)
        

    def deserialize(self, data):
        vals = data.split(',')
        self.i = 0
        def dfs():
            if vals[self.i] == 'N':
                self.i += 1
                return None
            node = TreeNode(int(vals[self.i]))
            self.i += 1
            node.left = dfs()
            node.right = dfs()

            return node
    
        return dfs()

        

# Your Codec object will be instantiated and called as such:
# ser = Codec()
# deser = Codec()
# ans = deser.deserialize(ser.serialize(root))