NERF++: ANALYZING AND IMPROVING NEURAL RADIANCE FIELDS分析和改进神经辐射场
目录
NERF++: ANALYZING AND IMPROVING NEURAL RADIANCE FIELDS分析和改进神经辐射场
ABSTRACT
1 INTRODUCTION
2 PRELIMINARIES
3 SHAPE-RADIANCE AMBIGUITY形状-辐射模糊度
4 INVERTED SPHERE PARAMETRIZATION反向球体参数化
NERF++: ANALYZING AND IMPROVING NEURAL RADIANCE FIELDS分析和改进神经辐射场
ABSTRACT
神经辐射场(NeRF)为各种捕捉设置实现了令人印象深刻的视图合成结果,包括有界场景的360°捕捉360◦ capture of bounded scenes以及有界和无界场景的前向捕捉forward-facing capture of bounded and unbounded scenes。NeRF将表示视图不变不透明度view-invariant opacity和视图相关颜色体积的view-dependent color volumes多层感知器(MLPs)拟合到一组训练图像,并基于体积绘制技术对新视图进行采样。在这份技术报告中,我们首先讨论了辐射场及其潜在的模糊性potential ambiguities,即形状辐射率的模糊性shape-radiance ambiguity,并分析了NeRF在避免这种模糊性方面的成功之处。第二,我们提出了一个参数化问题,它涉及到将NeRF应用于大规模、无边界3D场景中的360°物体特征。我们的方法在这种具有挑战性的场景中提高了视图合成的保真度。代码可在https://github.com/Kai-46/nerfplusplus.获得
1 INTRODUCTION
回忆一下你的上一个假期,在那里你拍了几张你最喜欢的地方的照片。现在在家里,你希望再次在这个特别的地方走动,如果只是虚拟的。这要求您在一个可能无限的场景中从不同的、自由放置的视点渲染同一个场景。这种新颖的视图合成任务是计算机视觉和图形学中的一个长期存在的问题(Chen & Williams,1993;Debevec等人,1996年;莱沃伊和汉拉汉,1996年;Gortler等人,1996年;Shum & Kang,2000年)。
最近,基于学习的方法已经导致了照片级的新颖视图合成的重大进展。特别是神经辐射场(NeRF)的方法已经引起了极大的关注(Mildenhall等人,2020)。NeRF是一个隐式的基于MLP的模型,它将5D向量(3D坐标加上2D观察方向)映射到不透明度和颜色值,通过将模型拟合到一组训练视图来计算。然后,所得到的5D函数可以用于利用传统的体绘制技术生成新的视图。
在本技术报告中,我们首先对NeRF中的潜在故障模式进行了分析,并分析了NeRF在实践中避免这些故障模式的原因。第二,我们提出了一种新的空间参数化方案novel spatial parameterization scheme,我们称之为反向球面参数化inverted sphere parameterization,它允许NeRF处理一类新的无界场景捕获captures of unbounded scenes。
图1:形状辐射模糊度(左)和无边界场景的参数化(右)。形状歧义Shape-radiance ambiguity:我们的理论分析表明,在缺乏显式或隐式正则化,一组训练图像可以独立于恢复几何(例如,不正确的场景几何Sˆ而不是正确的几何S∗)通过利用视图相关的辐射来模拟正确的几何的效果。无界场景的参数化Parameterization of unbounded scenes:使用标准参数化方案,要么只建模部分场景(红色轮廓),导致背景元素中的重要伪影,或(2)整个场景被建模(橙色轮廓),这导致由于有限的采样分辨率的细节的总体损失。
特别地,我们发现在理论上,在没有任何正则化的情况下,从一组训练图像优化5D函数会遇到不能推广到新的测试视图的临界退化解critical degenerate solutions。这种现象被封装在形状-辐射模糊度中shape-radiance ambiguity(图1,左),其中通过适当选择每个表面点的出射2D辐射outgoing 2D radiance,可以为任意不正确的几何形状完美地拟合一组训练图像。我们的经验表明,NeRF中使用的特定MLP结构在避免这种歧义方面发挥了重要作用,产生了令人印象深刻的综合新观点synthesize novel views的能力。我们的分析为NeRF令人印象深刻的成功提供了一个新的视角。
我们还解决了一个空间参数化问题,该问题出现在具有挑战性的场景中,包括在无界环境中围绕物体进行360°捕捉(图1,右侧)。对于360◦ captures,NeRF假设整个场景可以打包到一个有界的体积中,这对于大规模场景来说是有问题的:要么我们将场景的一小部分装进体积中,并对其进行详细采样,但完全无法捕捉背景元素;或者,我们将整个场景放入体积中,由于有限的采样分辨率,到处都缺少细节。我们提出了一种简单而有效的解决方案,该方案分别对前景和背景进行建模,利用反向球体场景参数化inverted sphere scene parameterization对无界3D背景内容进行建模解决了挑战。我们展示了坦克和寺庙数据集Tanks and Temples dataset(Knapitsch等人,2017年)和余等人(2016年)的光场数据集的真实世界捕捉的定量和定性结果。
总之,我们提出了一个关于NeRF如何设法解决形状-辐射模糊的分析,以及一个在360◦ captures情况下对无界场景参数化的补救措施。
2 PRELIMINARIES
给定静态场景的设定的多视图图像,NeRF重建表示软形状soft shape的不透明度场opacity field σ,以及表示依赖于视图的表面纹理的辐射场c。σ和c都隐式表示为多层感知器(MLPs);不透明度场作为3D位置x ∈ R3的函数来计算,并且辐射场由3D位置和观察方向d ∈ S2(即,单位3向量的集合)来参数化。因此,我们使用σ(x)来表示作为位置函数的不透明度,使用c(x,d)来表示作为位置和观察方向函数的辐射度。
理想情况下,σ应在不透明材料的地面真实表面位置达到峰值,在这种情况下,c降低到表面光场surface light field(Wood等人,2000)。给定n个训练图像,NeRF使用随机梯度下降通过最小化地面真实观察图像I和从相同视点处的σ和c渲染的预测图像I(σ,c)之间的差异来优化σ和c:
为了补偿网络的光谱偏差spectral bias并合成更清晰的图像,NeRF使用位置编码γ将x和d映射到它们的傅立叶特征(Tancik等人,2020年):
其中k是指定傅立叶特征向量的维度的超参数。
3 SHAPE-RADIANCE AMBIGUITY形状-辐射模糊度
NeRF对依赖于视图的外观进行建模的能力导致3D形状和辐射度之间的固有模糊性ambiguity,在没有正则化的情况下,这可能允许退化的解决方案。对于任意的、不正确的形状,可以表明存在一族辐射场,其完美地解释了训练图像,但是其对于新颖的测试视图的概括较差。
为了说明这种模糊性,想象对于给定的场景,我们将几何图形表示为一个单位球。换句话说,让我们将NeRF的不透明度场在单位球表面固定为1,在其他地方固定为0。然后,对于每个训练图像中的每个像素,我们将穿过该像素的光线与球体相交,并将交点处的辐射值(沿着光线方向)定义为该像素的颜色。这种人工构建的解决方案是一种有效的NeRF重建,与输入图像完全吻合。然而,这种解决方案合成新视图的能力非常有限:精确地生成这样的视图需要在每个表面点上重建任意复杂的视图相关函数。该模型不太可能精确地内插这样一个复杂的函数,除非训练视图非常密集,如在传统的光场渲染工作中(Buehler等人,2001;莱沃伊和汉拉汉,1996年;Gortler等人,1996年)。这种形状-辐射模糊性如图2所示。
图2:为了证明形状-辐射模糊性shape-radiance ambiguity,我们在合成数据集上预训练NeRF,其中不透明度场σ被优化以模拟不正确的3D形状(单位球体,而不是推土机形状),而辐射场c被优化以将训练射线与球体的交点和视图方向映射到它们的像素颜色。在本例中,我们使用3个MLP层来模拟视点相关的效果(参见图3中的MLP结构),并适合50个视点随机分布在一个半球上的合成训练图像。产生的不正确的解决方案很好地解释了训练图像(左边的两个图像),但是未能推广到新的测试视图(右边的两个图像)。
形状辐射歧义是指根据给出的训练视图,最后训练出的辐射场,不是正确的挖掘机的形状,而是可以拟合训练集的形状如球形,但是,对于测试集,该拟合出的错误辐射场不能正确生成图片。
NeRF为什么能避免这样的退化解degenerate solutions?我们假设两个相关因素拯救了NeRF:
- 不正确的几何形状迫使辐射场具有更高的内在复杂性(即,更高的频率),
- 而相反, NeRF的特定MLP结构隐含地编码了表面反射之前的平滑BRDF。
因素1:当σ偏离正确的形状时,c通常必须变成相对于d的高频函数,以重构输入图像。对于正确的形状,表面光场通常会平滑得多(事实上,对于朗伯材质是恒定的)。不正确的形状所需的更高的复杂性更难以用有限容量的MLP来表示。
因素2:特别是,NeRF的特定MLP结构编码了一个隐含的先验信息,有利于平滑的表面反射函数,其中c在任何给定的表面点x相对于d是平滑的。如图3所示,这种MLP结构不对称地处理场景位置x和观察方向d,d被注入到靠近MLP末端的网络中,这意味着在视图相关效果的创建中涉及较少的MLP参数以及较少的非线性激活。此外,用于对观察方向进行编码的傅立叶特征仅由低频分量组成,即,用于对d和x进行编码的γ4()和γ10()(见等式3)。换句话说,对于固定的x,辐射度c(x,d)相对于d具有有限的表现力。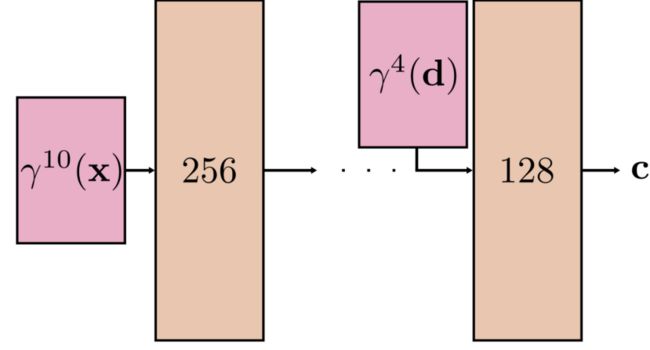
图3:用于建模辐射亮度c的NeRF MLP的结构
NeRF的特色MLP比普通的对称MLP效果更好
为了验证这一假设,我们进行了一项实验,用一个普通的MLP来表示c,它对称地对待x和d,即接受两者作为第一层的输入,并用γ10()进行编码,以消除网络结构中出现的涉及观察方向的任何隐含先验。如果我们用c的这个替代模型从头开始训练NeRF,我们观察到与NeRF的特殊MLP相比,测试图像质量下降,如图4和表1所示。这一结果与我们的假设相一致,即NeRF辐射c的MLP模型中反射率的隐式正则化有助于恢复正确的解。
图4:在DTU场景中(Jensen等人,2014;里格勒和科尔顿,2020),该图显示了用普通MLP替换NeRF的辐射场c模型的效果(同时保持σ的结构相同,并从头开始训练两个场)。普通的MLP损害了NeRF概括到新观点的能力。
表1:在DTU场景上(Jensen等人,2014),用普通的MLP取代NeRF的MLP显著减少了对新视图的泛化。我们使用与Riegler&Koltun(2020)相同的数据分割。左边的数字是插值interpolation,右边的数字是外推extrapolation。他们在背景被掩盖的完整图像上进行评估。
4 INVERTED SPHERE PARAMETRIZATION反向球体参数化
等式2中的体绘制公式在欧几里德深度上积分。当真实场景深度的动态范围很小时,可以用有限数量的样本在数值上很好地近似积分。然而,对于室外,360◦ captures 以附近物体为中心,同时观察周围环境,动态深度范围可以非常大,作为背景(建筑物、山脉、云等。)可以任意远。如此高的动态深度范围在NeRF的体积场景表示中导致了严重的分辨率问题,因为为了合成照片般逼真的图像,等式2在前景和背景区域都需要足够的分辨率,这很难通过根据3D空间的欧几里德参数化简单地采样点来实现。
图5:对于360◦捕获的无限场景,NeRF的空间参数化要么只建模场景的一部分,导致背景元素(a)中的重要工件,要么建模整个场景,并由于有限的采样分辨率(b).而遭受整体细节损失
图5展示了场景覆盖和捕捉细节之间的折衷tradeoff。在一个更受限制的场景中,所有相机都面向将相机与场景内容分开的平面,NeRF通过将欧几里得空间的子集(即,camera’s view frustum)投影映射到归一化的设备坐标(NDC) (McReynolds & Blythe,2005),并在该NDC空间中积分来解决这个分辨率问题。然而,这种NDC参数化也从根本上限制了可能的视点,因为它未能覆盖参考视图截锥reference view frustum外部的空间。
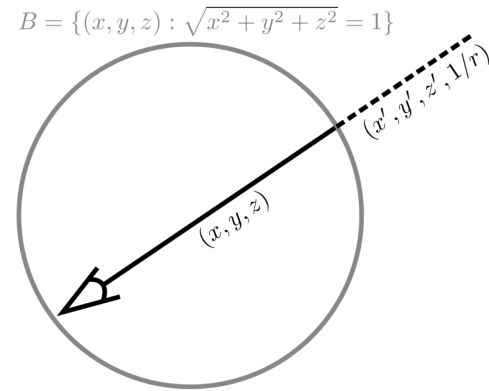
我们通过简化自由视图合成facilitates free view synthesis的反向球体参数化 inverted sphere parameterization来解决这一限制。在我们的表示中,我们首先将场景空间划分为两个体积,一个内部单位球体和一个由覆盖内部体积补集的反向球体表示的外部体积outer volume(参见图6中的说明和图7中以这种方式建模的场景的真实世界示例)。内部体积包含前景和所有摄像机,而外部体积包含环境的剩余部分。
图6: NeRF++对单位球内外的场景内容应用了不同的参数化。
这两个卷volumes是用两个独立的神经模型制作的。要渲染光线的颜色,需要单独进行光线投射raycast,然后进行最终合成。内部NeRF不需要重新参数化,因为场景的这一部分被很好地限制住了。对于外部NeRF,我们应用了一个反向球体参数化inverted sphere parametrization。
这不仅提高了数值的稳定性,而且考虑到了更远的对象应该获得更低的分辨率这一事实。我们可以直接光线投射这个4D有界体(只有3个自由度)来渲染相机光线的颜色。注意,前景和背景的合成相当于打破了等式2中的积分 分为两部分,integration inside the inner and outer volumes。特别是,考虑到射线r = o + td被单位球面分割成两段:第一段,t ∈ (0,t′)在球面内;在第二种情况下,t∈(t′,∞)在球面之外。我们可以重写等式2中的体绘制积分为
外体积的倒球面参数化具有直观的物理解释。它可以用一个虚拟摄像机来观察,它的像平面是场景原点的单位球面。因此,3D点(x,y,z)被投影到图像平面上的像素(x′,y′,z′),而项1/r ∈ (0,1)用作该点的(逆)深度或视差。从这个角度来看,仅适用于前向捕捉的NDC参数化与我们的表示相关,因为它使用虚拟针孔相机而不是球形投影表面。在这个意义上,我们的反向球体参数化与在最近的视图合成工作中提出的多球体图像(由嵌套的同心球体组成的场景表示,根据从球体中心的反向深度采样)的概念有关(Attal等人,2020;Broxton等人,2020年)。