LeetCode刷题笔记（Java）---第561-580题

前言

需要开通vip的题目暂时跳过

笔记导航

点击链接可跳转到所有刷题笔记的导航链接

561.数组拆分 I

给定长度为 2n 的整数数组 nums ，你的任务是将这些数分成 n 对, 例如 (a1, b1), (a2, b2), …, (an, bn) ，使得从 1 到 n 的 min(ai, bi) 总和最大。

返回该 最大总和 。

• 解答

  public int arrayPairSum(int[] nums) {
          Arrays.sort(nums);
          int res = 0;
          for(int i = 0;i < nums.length;i += 2){
              res += Math.min(nums[i],nums[i + 1]);
          }
          return res;
      }
  

• 分析

  1. 要使得两两组和的最小值之后的总和最大
  2. 那么就需要保证两两组和之间的差最小
  3. 所以理所当然的想到排序，然后两两之间进行组合。

• 提交结果[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-F9e8XfDg-1608689977065)(/Users/gongsenlin/Library/Application Support/typora-user-images/截屏2020-12-21 上午10.51.58.png)]

563. 二叉树的坡度

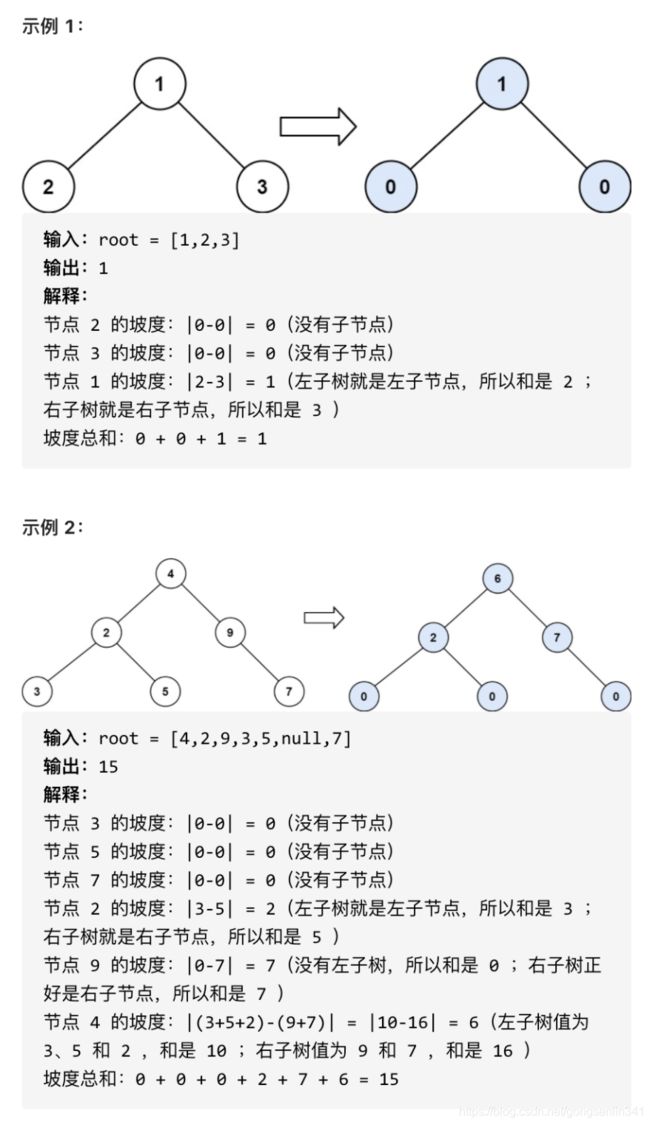
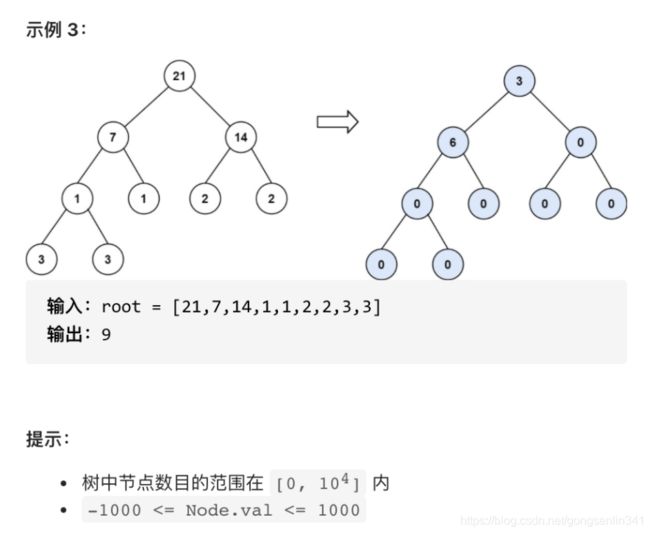
给定一个二叉树，计算 整个树 的坡度 。

一个树的 节点的坡度 定义即为，该节点左子树的节点之和和右子树节点之和的 差的绝对值 。如果没有左子树的话，左子树的节点之和为 0 ；没有右子树的话也是一样。空结点的坡度是 0 。

整个树 的坡度就是其所有节点的坡度之和。

• 解答

  int res = 0;
      public int findTilt(TreeNode root) {
          dfs(root);
          return res;
      }
  
      public int dfs(TreeNode root){
          if(root == null)return 0;
          int left = dfs(root.left);
          int right = dfs(root.right);
          res += Math.abs(left - right);
          return left + right + root.val;
      }
  

• 分析

  1. 递归的去计算，每个结点的总和。
  2. 一个结点的总和等于左子树+右子树+自身结点的数值。
  3. 在递归的过程中计算坡度，这样就可以得到所有结点的坡度总和。

• 提交结果

564. 寻找最近的回文数

给定一个整数 n ，你需要找到与它最近的回文数（不包括自身）。

“最近的”定义为两个整数差的绝对值最小。

• 解答

  public String mirroring(String s) {
          String x = s.substring(0, (s.length()) / 2);
          return x + (s.length() % 2 == 1 ? s.charAt(s.length() / 2) : "") + new StringBuilder(x).reverse().toString();
      }
      public String nearestPalindromic(String n) {
          if (n.equals("1"))
              return "0";
  
          String a = mirroring(n);
          long diff1 = Long.MAX_VALUE;
          diff1 = Math.abs(Long.parseLong(n) - Long.parseLong(a));
          if (diff1 == 0)
              diff1 = Long.MAX_VALUE;
  
          StringBuilder s = new StringBuilder(n);
          int i = (s.length() - 1) / 2;
          while (i >= 0 && s.charAt(i) == '0') {
              s.replace(i, i + 1, "9");
              i--;
          }
          if (i == 0 && s.charAt(i) == '1') {
              s.delete(0, 1);
              int mid = (s.length() - 1) / 2;
              s.replace(mid, mid + 1, "9");
          } else
              s.replace(i, i + 1, "" + (char)(s.charAt(i) - 1));
          String b = mirroring(s.toString());
          long diff2 = Math.abs(Long.parseLong(n) - Long.parseLong(b));
  
  
          s = new StringBuilder(n);
          i = (s.length() - 1) / 2;
          while (i >= 0 && s.charAt(i) == '9') {
              s.replace(i, i + 1, "0");
              i--;
          }
          if (i < 0) {
              s.insert(0, "1");
          } else
              s.replace(i, i + 1, "" + (char)(s.charAt(i) + 1));
          String c = mirroring(s.toString());
          long diff3 = Math.abs(Long.parseLong(n) - Long.parseLong(c));
  
          if (diff2 <= diff1 && diff2 <= diff3)
              return b;
          if (diff1 <= diff3 && diff1 <= diff2)
              return a;
          else
              return c;
      }
  

• 分析

  1. 考虑将字符串的前半部分反转的结果复制到后半部分。

  2. 存在两种特殊情况。若中间数字是0的情况下，例如10099，如果使用第一种反转的结果 得到的是10001

     可最近的回文字符串应该是9999，所以不妨将前一半字符串减1 得到99，然后再反转。

  3. 所以当遇到中间是0的情况下，需要将前一半字符串减1，然后反转。

  4. 同理 当遇到中间字符串是9的情况下，需要将前一半字符串加1，然后再反转

  5. 一共有3种可能的情况，所以需要每种情况都计算距离，然后返回最近的。

• 提交结果

565. 数组嵌套

索引从0开始长度为N的数组A，包含0到N - 1的所有整数。找到最大的集合S并返回其大小，其中 S[i] = {A[i], A[A[i]], A[A[A[i]]], … }且遵守以下的规则。

假设选择索引为i的元素A[i]为S的第一个元素，S的下一个元素应该是A[A[i]]，之后是A[A[A[i]]]… 以此类推，不断添加直到S出现重复的元素。

• 解答

  public int arrayNesting(int[] nums) {
          int len = nums.length;
          int[] visited = new int[len];
          int res = 0;
          int temp = 0;
          for(int i = 0;i < len;i++){
              temp = 0;
              if(visited[i] == 0){
                  int p = i;
                  temp = 1;
                  visited[i] = temp;
                  while(visited[nums[p]] == 0){
                      temp++;
                      p = nums[p];
                      visited[p] = 1;
                  }
                  res = Math.max(res,temp);
              }
          }
          return res;
      }
  

• 分析

  1. 因为不存在重复的元素，所以此题就比较简单了
  2. 寻找一个最大的连通路径，各个连通路径之间是不会重叠的。
  3. 所以用visited来记录已经走过的路，并计算路径的长度。
  4. 留下连通路径的最大值作为答案。

• 提交结果

566. 重塑矩阵

在MATLAB中，有一个非常有用的函数 reshape，它可以将一个矩阵重塑为另一个大小不同的新矩阵，但保留其原始数据。

给出一个由二维数组表示的矩阵，以及两个正整数r和c，分别表示想要的重构的矩阵的行数和列数。

重构后的矩阵需要将原始矩阵的所有元素以相同的行遍历顺序填充。

如果具有给定参数的reshape操作是可行且合理的，则输出新的重塑矩阵；否则，输出原始矩阵。

• 解答

  public int[][] matrixReshape(int[][] nums, int r, int c) {
          int row = nums.length;
          int col = nums[0].length;
          if(row * col != r * c)return nums;
          int[][] res = new int[r][c];
          int rIndex = 0;
          int cIndex = 0;
          for(int i = 0;i < row;i++){
              for(int j= 0;j < col;j++){
                  res[rIndex][cIndex] = nums[i][j];
                  if(cIndex <c-1)cIndex++;
                  else{
                      rIndex++;
                      cIndex=0;
                  }
              }
          }
          return res;
      }
  

• 分析

  1. 首先判断原来矩阵的长宽的乘积是否等于r*c，若不等的话直接返回nums
  2. 遍历nums，将元素一个个的填入到新的矩阵中

• 提交结果

567. 字符串的排列

给定两个字符串 s1 和 s2，写一个函数来判断 s2 是否包含 s1 的排列。

换句话说，第一个字符串的排列之一是第二个字符串的子串。

• 解答

  public boolean checkInclusion(String s1, String s2) {
          int len1 = s1.length();
          int len2 = s2.length();
          if(len2 < len1)return false;
          int[] count = new int[26];
          int[] dif = new int[26];
          int difNumber = 0;
          for(int i = 0;i < len1;i++){
              char cur = s1.charAt(i);
              count[cur - 'a']++;
          }
          for(int i = 0;i < len1;i++){
              char cur = s2.charAt(i);
              if(count[cur - 'a'] > 0){
                  dif[cur - 'a']++;
                  if(dif[cur-'a'] > count[cur - 'a'])
                      difNumber++;
              }else difNumber++;
          }
          if(difNumber == 0)return true;
          for(int i = 1;i < len2 - len1 + 1;i++){
              char cur = s2.charAt(i-1);//移出滑动窗口的值
              if(count[cur-'a'] > 0){
                  dif[cur-'a']--;
                  if (dif[cur-'a'] < count[cur-'a']) {
                      difNumber++;
                  }
              }
              char yiru = s2.charAt(i + len1 -1);
              if(count[yiru-'a'] > 0){
                  dif[yiru-'a']++;
                  if(dif[yiru-'a'] <= count[yiru-'a'])
                      difNumber--;
                  if(difNumber == 0)return true;
              }
          }
          return false;
      }
  

• 分析

  1. 滑动窗口实现，窗口大小为s1的长度
  2. 数组count 用来记录s1中字符出现的个数
  3. 数组dif用来记录s2 滑动窗口内 和s1中出现字符相同的字符的个数。
  4. difNumber 用来记录滑动窗口内的字符和s1中的字符匹配度相差的个数。
  5. 当difNumber等于0的时候，说明窗口内的字符与s1匹配 返回true。
  6. 第一个for循环，统计s1中字符的个数
  7. 第二个for循环，统计初始窗口内，与s1中字符相同的字符出现的次数，以及相差的匹配个数difNumber
  8. 第三个for循环，用来移动滑动窗口，根据移出与移入的字符，来修改dif数组和difNumber

• 提交结果

572. 另一个树的子树

给定两个非空二叉树 s 和 t，检验 s 中是否包含和 t 具有相同结构和节点值的子树。s 的一个子树包括 s 的一个节点和这个节点的所有子孙。s 也可以看做它自身的一棵子树。

• 解答

  public boolean isSubtree(TreeNode s, TreeNode t) {
          if(s == null)return false;
          if(t == null)return false;
          return isSubtree(s.left,t) || isSubtree(s.right,t) || isSame(s,t);
      }
  
      public boolean isSame(TreeNode p,TreeNode t){
          if(p == null && t == null)return true;
          if(p == null || t ==null)return false;
          if(p.val != t.val)return false;
          return isSame(p.left,t.left) && isSame(p.right,t.right);
      }
  

• 分析

  1. 递归实现
  2. 当s为空或者t为空的时候，返回false
  3. 判断s的左子树是否存在和t相同的结构 或判断s的右子树是否存在和t相同的结构 或者判断s和t是否相同。
  4. s和t是否相同用isSame来判断。
  5. 若当前结点都为空，则返回true
  6. 若有一个不为空，则返回false
  7. 若当前结点的值不同 返回false
  8. 递归的判断 左子树和右子树是否相同，来确定两棵树是否相同。

• 提交结果

575. 分糖果

给定一个偶数长度的数组，其中不同的数字代表着不同种类的糖果，每一个数字代表一个糖果。你需要把这些糖果平均分给一个弟弟和一个妹妹。返回妹妹可以获得的最大糖果的种类数。

给定一个偶数长度的数组，其中不同的数字代表着不同种类的糖果，每一个数字代表一个糖果。你需要把这些糖果平均分给一个弟弟和一个妹妹。返回妹妹可以获得的最大糖果的种类数。

• 解答

  //方法1
  public int distributeCandies(int[] candyType) {
          Set<Integer> set = new HashSet<>();
          for(int c : candyType){
              set.add(c);
          }
          if(set.size() < candyType.length/2){
              return set.size();
          }else{
              return candyType.length/2;
          }
      }
  //方法2
  public int distributeCandies(int[] candyType) {
          int[] candy = new int[200001];
          int num = 0;
          for(int c : candyType){
              candy[c + 100000]++;
              if(candy[c+100000] == 1)num++;
          }
          if(num < candyType.length/2){
              return num;
          }else{
              return candyType.length/2;
          }
      }
  

• 分析

  1. 计算糖果的种类，若种类数小于糖果总数的一半，那么妹妹可以获得所有种类的糖果。
  2. 若种类数大于糖果总数的一半，那么妹妹可以获得的种类数目就是糖果数目的一半。
  3. 方法1 用set来计算糖果的种类数目
  4. 方法2 用数组来计算糖果的种类数目

• 提交结果

  方法1

  方法2

576. 出界的路径数

给定一个 m × n 的网格和一个球。球的起始坐标为 (i,j) ，你可以将球移到相邻的单元格内，或者往上、下、左、右四个方向上移动使球穿过网格边界。但是，你最多可以移动 N 次。找出可以将球移出边界的路径数量。答案可能非常大，返回 结果 mod 109 + 7 的值。

• 解答

  //方法1
  long mod = 1000000007;
      public int findPaths(int m, int n, int N, int i, int j) {
          long[][][] dp = new long[m][n][N+1];//dp[i][j]最多移动N步到边界的路径数量。
          return (int)findPaths(dp,i,j,N,m,n);
      }
  
      public long findPaths(long[][][] dp,int i,int j,int N,int m,int n){
          if(i < 0 || i >=m || j < 0 || j >= n)return 1;
          if(N == 0)return 0;
          if(dp[i][j][N] != 0)return dp[i][j][N];
          dp[i][j][N] += findPaths(dp,i-1,j,N-1,m,n);
          dp[i][j][N] += findPaths(dp,i+1,j,N-1,m,n);
          dp[i][j][N] += findPaths(dp,i,j-1,N-1,m,n);
          dp[i][j][N] += findPaths(dp,i,j+1,N-1,m,n);
          return dp[i][j][N] % mod;
      }
  //方法2
  public int findPaths(int m, int n, int N, int i, int j) {
          long mod = 1000000007;
          long[][][] dp = new long[m+2][n+2][N+1];
          for(int k = 0;k < m+2;k++){
              dp[k][0][0] = 1;
              dp[k][n+1][0] = 1;
          }
          for(int k = 0;k < n+2;k++){
              dp[0][k][0] = 1;
              dp[m+1][k][0] = 1;
          }
          for(int nn = 1;nn <= N;nn++){
              for(int k = 1;k < m+1;k++){
                  for(int l = 1;l < n+1;l++){
                      dp[k][l][nn] = (dp[k-1][l][nn-1] + dp[k+1][l][nn-1] + dp[k][l-1][nn-1] + dp[k][l+1][nn-1]) % mod;
                  }
              }
          }   
          long res = 0;
          for(int nn = 1;nn <=N;nn++){
              res = (res + dp[i+1][j+1][nn]) % mod;
          }
          return (int)res;
      }
  

• 分析

  1. 方法1递归超时

  2. 方法2 动态规划

  3. dp[i] [j] [k] 表示 在i j的位置走k步出界的路径数量。

  4. 动态转移方程就是4个方向走k-1步出界的路径数量 也就是

     dp[k] [l] [nn] = (dp[k-1] [l] [nn-1] + dp[k+1] [l] [nn-1] + dp[k] [l-1] [nn-1] + dp[k] [l+1] [nn-1]) % mod;

  5. 初始条件，出界边界 = 1

  6. 最后的结果就是 将dp[i] [j] [1] ~ dp[i] [j] [N] 累加起来

• 提交结果