区间dp+三维状态，POJ1390 Blocks

目录

一、题目

1、题目描述

2、输入格式

​3、输出格式

4、原题链接

二、解题报告

1、思路分析

朴素区间dp思维

二维升三维

2、复杂度

3、代码详解

---

一、题目

1、题目描述

Some of you may have played a game called 'Blocks'. There are n blocks in a row, each box has a color. Here is an example: Gold, Silver, Silver, Silver, Silver, Bronze, Bronze, Bronze, Gold.
The corresponding picture will be as shown below:

Figure 1

If some adjacent boxes are all of the same color, and both the box to its left(if it exists) and its right(if it exists) are of some other color, we call it a 'box segment'. There are 4 box segments. That is: gold, silver, bronze, gold. There are 1, 4, 3, 1 box(es) in the segments respectively.

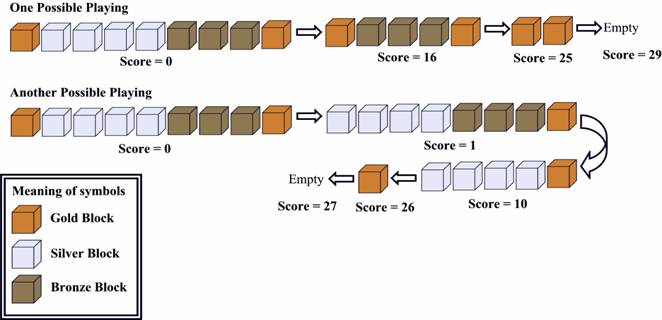
Every time, you can click a box, then the whole segment containing that box DISAPPEARS. If that segment is composed of k boxes, you will get k*k points. for example, if you click on a silver box, the silver segment disappears, you got 4*4=16 points.

Now let's look at the picture below:

Figure 2

The first one is OPTIMAL.

Find the highest score you can get, given an initial state of this game.

2、输入格式

The first line contains the number of tests t(1<=t<=15). Each case contains two lines. The first line contains an integer n(1<=n<=200), the number of boxes. The second line contains n integers, representing the colors of each box. The integers are in the range 1~n.

Sample Input

2
9
1 2 2 2 2 3 3 3 1
1
1

​3、输出格式

For each test case, print the case number and the highest possible score.

Sample Output

Case 1: 29
Case 2: 1

4、原题链接

1390 -- Blocks (poj.org)

---

二、解题报告

1、思路分析

朴素区间dp思维

乍一看觉得是比较经典的区间dp板子题，设计状态f[l][r]为删除区间[l , r]可以获得的最大得分，然后想当然的给出了转移方程

1. f[l][r] = max(f[l][r] , f[l][i] + f[i + 1][r])，即分成两个子区间求和
2. f[l][r] = max(f[l][r] , f[i][j] + len * len)，a[l , i - 1] = a[j + 1 , r] = a[l] = a[r]，两端相等的连续块之间的先合并，再把连续块合并

但是这样有个问题，以第二个方程为例，区间两侧的连续相等块也可以跟[i, j]内的零散的相等块拼接合并，这个转移方程没有考虑到区间内的零散块，但是二维的状态使得我们无法获取区间内的细节，所以二维状态无法解决问题，所以我们尝试升维

二维升三维

如果设计三维状态，我们状态转移不能超过O(n)，要把时间复杂度控在O(n^4)，我们怎样设计状态，怎样转移呢？

我们处理数据时，对于连续区间给他合并为一个区间，这样存储箱子的数组a[i]都对应一个cnt[i]代表a[i]含有多少个颜色为a[i]箱子

设计f[l][r][k]为区间[l , r]右边有k个和a[r]相等的元素，删除[l , r]能够获得的最大得分

那么我们有两种选择：

把a[r]跟右边的相等块拼接，不管左边的，那么

f[l][r][k] = dfs(l, r - 1, 0) + (cnt[r] + k) * (cnt[r] + k)

把a[r]跟左边区间内的相等块拼接，再跟右边的相等块合并

f[l][r][k] = max(f[l][r][k], dfs(l, i, cnt[r] + k) + dfs(i + 1, r - 1, 0))

要理解这两个转移方程需要理解一个细节就是a[r]想跟右边拼接的前提就是右边和a[r]不相等的块都已经消除完了，这就是为什么我们方程转移的时候传给右边区间的k都是0

PS:不要开long long！！！

2、复杂度

时间复杂度： O(n^4) 空间复杂度：O(n^3)

3、代码详解

​

#include 
#include 
#include 
#include 
using namespace std;
#define IOTIE ios::sync_with_stdio(false), cin.tie(0), cout.tie(0);
// #define int long long
#define N 205
int f[N][N][N], n, a[N], cnt[N], t = 0, tot;
int dfs(int l, int r, int k)
{
    if (l > r)
        return 0;
    if (l == r)
        return (cnt[r] + k) * (cnt[r] + k);
    if (~f[l][r][k])
        return f[l][r][k];
    int &res = f[l][r][k] = dfs(l, r - 1, 0) + (cnt[r] + k) * (cnt[r] + k);
    for (int i = l; i < r; i++)
        if (a[r] == a[i])
            res = max(res, dfs(l, i, cnt[r] + k) + dfs(i + 1, r - 1, 0));
    return res;
}

void solve()
{
    memset(f, -1, sizeof(f)), memset(cnt, 0, sizeof(cnt)), a[tot = 0] = -1;
    int x;
    cin >> n;
    for (int i = 1; i <= n; i++)
    {
        cin >> x;
        if (x == a[tot])
            cnt[tot]++;
        else
            a[++tot] = x, cnt[tot]++;
    }
    cout << "Case " << ++t << ": " << dfs(1, tot, 0) << '\n';
}
signed main()
{
    IOTIE
    // freopen("in.txt", "r", stdin);
    int _ = 1;
    cin >> _;
    while (_--)
        solve();
    return 0;
}