密码学理论11：公钥加密

公钥加密概述

一方（接收方）生成一对密钥（pk，sk），分别称为公钥和私钥。发件人使用公钥加密消息；接收方使用私钥解密生成的密文。

• 当 Alice 得知 Bob 想与她通信时，她可以生成 (pk, sk)（假设她还没有这样做），然后将 pk 明文发送给 Bob。
• Alice 独立于任何特定的发送者预先生成 (pk, sk)。然后她公开发布pk。

优势：

1. 公钥加密（在某种程度上）解决了密钥分发问题，因为通信双方不需要在通信之前秘密共享密钥。即使他们之间的所有通信都被监视，两方也可以秘密通信。

2. 当单个接收方与 N 个发送方通信时，接收方存储单个私钥 sk 比共享、存储和管理 N 个不同的密钥（即每个发送方一个）要方便得多。

劣势：

1. 公钥加密方案允许任何人充当发送者，当接收者只想从一个特定的个人接收消息时，这可能是一个缺点。

2. 主要缺点是它比私钥加密慢大约 2 到 3 个数量级。

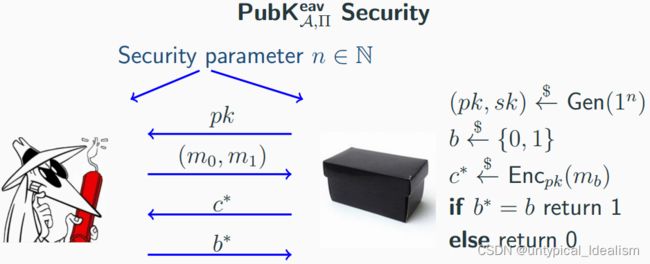
针对选择明文攻击的安全性

 公钥加密方案 Π = (Gen, Enc, Dec) 在存在窃听者的情况下具有不可区分的加密，如果对于所有概率多项式时间对手 A 都有一个可忽略的函数 negl 使得：

公钥加密

定义

公钥加密方案是 PPT 算法的三元组（Gen、Enc、Dec）：

1. 密钥生成算法 Gen 以安全参数 1^n 作为输入并输出一对密钥 (pk, sk)（消息空间 M 隐含在公钥中）。

2. 加密算法 Enc 将公钥 pk 和来自某个消息空间的消息 m 作为输入。它输出密文 c，我们将其写为 c ← Encpk(m)。 （我们也经常写c ← Enc(m, pk)）

3. 确定性解密算法Dec以私钥sk和密文c为输入，输出消息m或特殊符号⊥表示失败。我们将其写为 m := Decsk(c)。 （我们也经常写 m := Dec(c, sk)）。

• 如果公钥加密方案在存在窃听者的情况下具有无法区分的加密，则它是 IND-CPA 安全的。
• 没有公钥加密方案可以完全保密。（依赖于困难问题）
• 没有确定性公钥加密方案是 IND-CPA 安全的。
• 如果公钥加密方案 Π 是 IND-CPA 安全的，那么它也具有不可区分的多重加密。

防止选择密文攻击的安全性

 公钥加密方案 Π = (Gen, Enc, Dec) 在选择密文攻击下具有不可区分的加密（或者是 CCA 安全的）如果对于所有概率多项式时间对手 A 有一个可忽略的函数 negl 使得：

混合加密

 密钥封装机制

密钥封装机制 (KEM) 是 PPT 算法的三元组（Gen、Encaps、Decaps）：

1. 密钥生成算法 Gen 以安全参数 1^n 作为输入，输出一对密钥 (pk, sk)（密钥长度至少为 n，n 可由 pk 确定）。

2. 封装算法 Encaps 将公钥 pk 和安全参数 1^n 作为输入。它输出密文 c 和密钥 k ∈ {0, 1}^p(n) ，其中 p 是密钥长度。我们将其写为 (c, k) ← Encapspk(1^n)（或 (c, k) ← Encaps(1^n, pk)）。

3. 确定性解封装算法Decaps以私钥sk和密文c为输入，输出密钥k或特殊符号⊥表示失败。我们将其写为 k := Decapssk(c)（或 k := Decaps(sk, c)）。

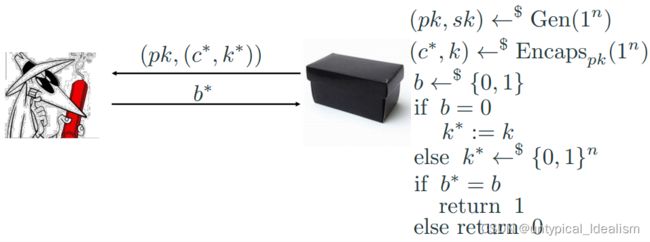
KEM 的安全定义 (IND-CPA)

 密钥封装机制 Π = (Gen, Enc, Dec) 是 IND-CPA 安全的，如果对于所有 PPT 对手 A 都有一个可忽略的函数 negl：

给定任何具有消息空间 M 的 PKE 方案Π = (Gen, Enc, Dec) ，可以构造一个 KEM Π ′ = (Gen′ , Encaps, Decaps) 如下：

• Π ′ .Gen′ (1^n ): Run (pk, sk) ← Π.Gen(1^n )
• Π ′ .Encapspk(1^n ): Choose k ←$ M, compute c ← Π.Encpk(k) and output (c, k)
• Π ′ .Decapssk(c): Output Π.Decsk(c)

•  给定 KEM 和 DEM（对称加密方案），我们可以轻松构建混合加密方案
• 在实践中，此类方案比纯 PKE 方案更有效——一旦消息需要多次 PKE 调用

令 Π = (Gen, Encaps, Decaps) 为密钥长度为 n 的 KEM，令 Π ′ = (Gen′ , Enc′ , Dec′ ) 为私钥加密 (DEM) 方案。我们构造一个公钥加密方案 Πhy = (Genhy, Enchy, Dechy) 如下：

1. Genhy：在输入 1^n 输出 (pk, sk) ← Gen(1^n )
2. Enchy：输入公钥 pk 和消息 m ∈ {0, 1} ∗ ：(c, k) ← Encapspk(1^n)；c ′ ← Enc′ k (m)；（c,c'）
3. Dechy：在输入私钥 sk 和密文 (c, c ′ ) 时：k := Decapssk(c)；m := Dec′ k (c ′ )

定理：

—如果 Π 是 CPA 安全的 KEM 并且 Π ' 是在存在窃听者的情况下具有不可区分的加密的对称加密方案，则 Πhy 是 CPA 安全的公钥加密方案。

—如果 Π 是一个 CCA 安全的 KEM 并且 Π ' 是一个 CCA安全的对称加密方案，那么 Πhy 是一个 CCA安全的公钥加密方案。

ElGamal加密

 采用 DH KE 协议并固定 Alice 的“第一条消息”g^a（连同组参数）作为她的公钥（a 是她的私钥）。为了向 Alice 加密，Bob 选择临时密钥g^b，使用 K 作为一次一密来加密消息 M ∈ G 并另外发送 g^b 。

在存在窃听者的情况下安全的任何 KE 协议都会产生 IND-CPA 安全的PKE。

• Gen(1n )：(G, q, g) ← G(1n )，选择 x $ ← Zq，计算 y := g^x 并输出 (sk, pk) := ((G, q, g, x), (G, q, g, y))。
• Enc(m, pk)：在输入 m ∈ G 和 pk = (G, q, g, y) 时，选择 r $ ← Zq，计算并输出 C := (g^r , m · y^r )。
• Dec(C, sk)：在输入 C = (C1, C2) 和 sk = (G, q, g, x) 时，计算并输出 m := C2 · (C1^x )^−1。
• 正确性：C2 ·(C1^x )^−1 = m · y^r ·((g^r)^x)^−1 = m·y^r·(y^r)^−1 = m · 1 = m。

安全性分析

引理：设 G 是一个有限群，m ∈ G 是任意的。然后均匀选择k ∈ G 则 k ′ := k·m 与 k ′ ∈ G 具有相同的分布。换句话说，对于任何 g ′ ∈ G 我们有：

在 ElGamal 中，密文是 C := (g^r , m · y^r ) 其中 y = g^x 是公钥。使用引理，我们构建了一个替代的 ElGamal “加密方法”，我们使用随机密钥 g^z 来加密：

• 这里密文的形式为 C := (g^r , m · g^z )。
• 敌手不知道 g^z 的值，即 m 是信息论上隐藏的，敌手只能猜测挑战位。

可证明（在 DDH 假设下）：在 IND-CPA 游戏中，没有敌手可以检测到我们修改了 ElGamal 加密方法。

性质

1. 同态性
2. 完美重随机性
3. 密钥隐私

RSA加密

• Gen()：生成RSA参数。

  在输入 1^n 上，输出模数 N，它是两个 n 位素数的乘积；随机选择 e，其中 1 < e < ϕ(N) 且gcd(e, ϕ(N)) = 1；计算d满足 ed = 1 mod ϕ(N)。

  pk = (N, e), sk = (d)

• Enc(pk, m)：c = m^e mod N

• Dec(sk, c)：m := c^d mod N

——教科书式的RSA是不安全的