数据结构之二叉树

目录

清晨

树的定义

节点间关系

树的层数

---

清晨

清晨，拉斯科尔尼科夫独自在家看起了电影《阿凡达》。发现电影里提到一颗高达900英尺的参天大树，是那个潘多拉星球的纳威人的家园。突然想起了今天的二叉树还没学,索性看完再学。

无论多高多大的树，也是从小到大，由根到叶，一点一点成长起来的。俗话说：十年树木，百年树人，可一颗大树又何止是十年这样容易。

树的定义

1.只能有一个根节点。

2.可以有无限个不相交的子节点。

3.节点的度：节点拥有的子树称为节点的度。度为0的节点称为叶节点，度不为0的节点称为分支节点。

定义一个树的结构体

typedef char BTDateType;//把char换个名字
//创建一个树的结构体
typedef struct BinaryTreeNode
{
	BTDateType _data;                    //根
	struct BinaryTreeNode* _left;   //左树
	struct BinaryTreeNode* _right;//右树
}BTNode;

创建伪树代码

//创建伪树
BTNode* GreateNode(BTDateType x)
{
	BTNode* Node = (BTNode*)malloc(sizeof(BTNode));
	Node->_data = x;
	Node->_left = NULL;
	Node->_right = NULL;
	return Node;
}

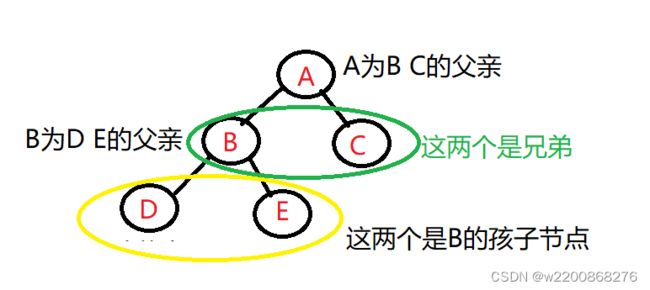
节点间关系

节点的子树的根为该节点的孩子，相应地，该节点为孩子的双亲。同一个双亲的孩子之间为兄弟。节点的祖先是从根到该节点所经分支上的所以节点。

树的层数

根为第一层

根的孩子为第二层，上一层加一就是下一层的层数。

树中节点的最大层次称为树的深度或高度。

高度为3的树

求第k个节点数代码

//查找第k个节点个数
int BinaryTreeLeve1KSize(BTNode* root, int k)
{
	if (root == NULL)
		return;
	if (k == 1)
		return 1;
	return BinaryTreeLeve1KSize(root->_left, k - 1) +
		BinaryTreeLeve1KSize(root->_right, k - 1);
}

求树的节点数代码

//求树有多少节点
//接收树和用于求节点个数的值
void TreeSize(BTNode* root,int *psize)
{
	if (root == NULL)//空就返回
	{
		return 0;
	}
	else
	{
		(*psize)++;
		TreeSize(root->_left, psize);//不是空就递归
		TreeSize(root->_right, psize);
	}
}

先序遍历树

遍历遵循：先根再左子树然后右子树

//采取先序方式遍历树
void PrevOrder(BTNode* root)
{
	if (root == NULL)
	{
		printf("NULL ");
		return;
	}
	printf("%c ", root->_data);
	PrevOrder(root->_left);//递归左
	PrevOrder(root->_right);//递归右
}

全部代码如下

#define  _CRT_SECURE_NO_WARNINGS 1
#include
#include

typedef char BTDateType;//把char换个名字
//创建一个树的结构体
typedef struct BinaryTreeNode
{
	BTDateType _data;                    //根
	struct BinaryTreeNode* _left;   //左树
	struct BinaryTreeNode* _right;//右树
}BTNode;

//求树有多少节点
//接收树和用于求节点个数的值
void TreeSize(BTNode* root,int *psize)
{
	if (root == NULL)//空就返回
	{
		return 0;
	}
	else
	{
		(*psize)++;
		TreeSize(root->_left, psize);//不是空就递归
		TreeSize(root->_right, psize);
	}
}

//求树的节点数,第二种方式
int TreeSize2(BTNode* root)
{
	if (root == NULL)
	{
		return 0;
	}
	else
		return 1 + TreeSize2(root->_left) + TreeSize2(root->_right);
}

//求树的叶子节点个数·
int TreeLeafSize(BTNode* root)
{
	if (root == NULL)
	{
		return 0;
	}
	if (root->_left == NULL && root->_right == NULL)
	{
		return 1;
	}
	return TreeLeafSize(root->_left) + TreeLeafSize(root->_right);
}

//采取先序方式遍历树
void PrevOrder(BTNode* root)
{
	if (root == NULL)
	{
		printf("NULL ");
		return;
	}
	printf("%c ", root->_data);
	PrevOrder(root->_left);//递归左
	PrevOrder(root->_right);//递归右
}
//中序
void InOrder(BTNode* root)
{
	if (root == NULL)
	{
		printf("NULL ");
		return;
	}
	InOrder(root->_left);
	printf("%c ", root->_data);
	InOrder(root->_right);
}
//后序
void PostOrder(BTNode* root)
{
	if (root == NULL)
	{
		printf("NULL ");
		return;
	}
	PostOrder(root->_left);
	PostOrder(root->_right);
	printf("%c ", root->_data);
}

//查找第k个节点个数
int BinaryTreeLeve1KSize(BTNode* root, int k)
{
	if (root == NULL)
		return;
	if (k == 1)
		return 1;
	return BinaryTreeLeve1KSize(root->_left, k - 1) +
		BinaryTreeLeve1KSize(root->_right, k - 1);
}

//二叉树查找值为x的节点
BTNode* BinaryTreeFind(BTNode* root, BTDateType x)
{
	if (root == NULL)
		return;
	if (root->_data == x)
		return root;
	BTNode* node = BinaryTreeFind(root->_left, x);
	if (node)
		return node;
	node = BinaryTreeFind(root->_right, x);
	if (node)
		return node;
}

//销毁树
void DestoryTree(BTNode* root)
{
	if (root == NULL)
		return;
	DestoryTree(root->_left);
	DestoryTree(root->_right);
	free(root);
}
//创建伪树
BTNode* GreateNode(BTDateType x)
{
	BTNode* Node = (BTNode*)malloc(sizeof(BTNode));
	Node->_data = x;
	Node->_left = NULL;
	Node->_right = NULL;
	return Node;
}

int main()
{
	BTNode* A = GreateNode('A');
	BTNode* B = GreateNode('B');
	BTNode* C = GreateNode('C');
	BTNode* D = GreateNode('D');
	BTNode* E = GreateNode('E');
	BTNode* F = GreateNode('F');
	BTNode* G = GreateNode('G');
	A->_left = B;
	A->_right = C;
	B->_left = D;
	B->_right = E;
	C->_left = F;
	C->_right = G;

	PrevOrder(A);
	printf("\n");
	InOrder(A);
	printf("\n");
	PostOrder(A);
	
	printf("\nTreeSize2: %d", TreeSize2(A));//树的节点个数
	printf("\nTreeLeafSize: %d", TreeLeafSize(A));//叶子节点个数
	printf("\nBinaryTreeLeve1KSize: %d", BinaryTreeLeve1KSize(A, 2));//第k层节点数
	//printf("\nBinaryTreeFind: %c", BinaryTreeFind(A, C));
	//int sizea = 0;
	//TreeSize(A, &sizea);
	//printf("\n%d", sizea);
	DestoryTree(A);
	return 0;
}