代码随想录算法训练营第四天| Leetcode 24. 两两交换链表中的节点、19.删除链表的倒数第N个节点、160. 链表相交 、142.环形链表II

Leetcode 24. 两两交换链表中的节点

题目链接：Leetcode 24. 两两交换链表中的节点

题目描述：

给定一个链表，两两交换其中相邻的节点，并返回交换后的链表。

你不能只是单纯的改变节点内部的值，而是需要实际的进行节点交换。

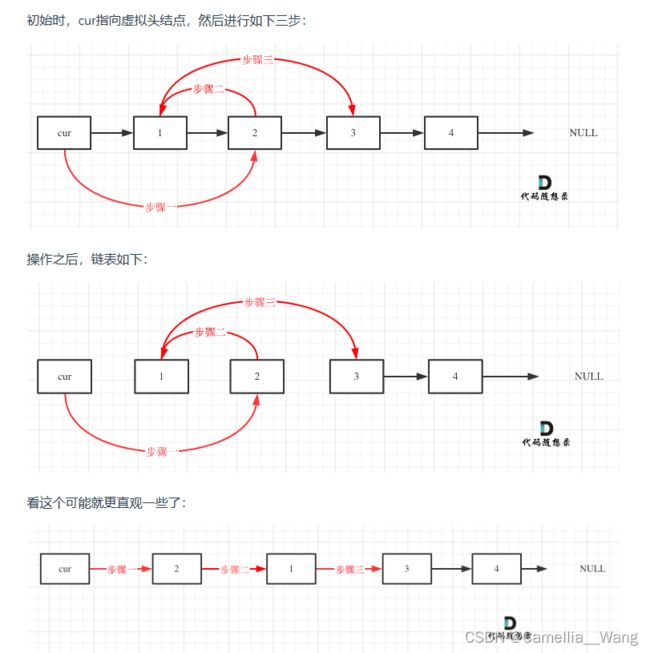
思路：本题的重点两两交换，而由于交换这两个节点需要先找到第一个节点的前一个节点，而头节点又没有前一个节点，因此本题构建一个虚拟头节点是一个很好的方法。个人体会，对于任何抽象的模拟过程，手动模拟画图是最好的理解方式。

注：以上图片来源于《代码随想录》

以下是代码实现：

class Solution {
public:
    ListNode* swapPairs(ListNode* head) {
        ListNode* dummyHead = new ListNode(0);
        dummyHead->next = head;
        ListNode* cur = dummyHead;
        //警惕这里的判断条件，连续两个->要注意第一个next不是空节点
        while (cur->next != nullptr && cur->next->next != nullptr) {
            //至于这里的写法大同小异，只要保证移动指针顺序正确即可
            ListNode* temp = cur->next;

            cur->next = temp->next;
            temp->next = cur->next->next;
            cur->next->next = temp;
            //不要忘了更新cur指针
            cur = cur->next->next;
        }
        return dummyHead->next;
    }
};

Leetcode 19.删除链表的倒数第N个节点

题目链接：Leetcode 19.删除链表的倒数第N个节点

题目描述：给你一个链表，删除链表的倒数第 n 个结点，并且返回链表的头结点。

思路：这道题最容易想到的方法就是先遍历一遍链表统计链表长度，然后循环n次即可。

第一种方法：利用链表长度找到删除节点

class Solution {
public:
    int getlen(ListNode* head) {
        int len = 0;
        while (head) {
            ++len;
            head = head->next;
        }
        return len;
    }
    ListNode* removeNthFromEnd(ListNode* head, int n) {
        ListNode* dummyHead = new ListNode(0, head);
        int len = getlen(head);
        ListNode* cur = dummyHead;
        //注意节点序号从1开始（一定要看清楚每道题的起始序号）
        //这里用++i或者i++的目的是最后让cur指向被删除元素的前一个元素
        for (int i = 1; i < len - n + 1; i++) {
            cur = cur->next;
        }
        //删除节点基本操作
        cur->next = cur->next->next;
        ListNode* res = dummyHead->next;
        delete dummyHead;
        return res;
    }
};

• 时间复杂度：O(L)，其中 L 是链表的长度。

• 空间复杂度：O(1)。

费劲心思求出链表长度之后，由于本题的进阶是寻找只需一次循环的方法，不禁联想到栈的先进后出的性质。尽管利用栈可以仅需一次循环，但是代价是增大了空间复杂度

第二种方法：利用栈的性质找到删除节点

class Solution {
public:
    ListNode* removeNthFromEnd(ListNode* head, int n) {
        ListNode* dummyHead = new ListNode(0, head);
        stack st;
        ListNode* cur = dummyHead;
        while (cur) {
            st.push(cur);
            cur=cur->next;
        }
        for (int i = 0; i < n; i++) {
            st.pop();
        }
        ListNode* prev = st.top();
        prev->next = prev->next->next;
        ListNode* res = dummyHead->next;
        delete dummyHead;
        return res;
    }
};

• 时间复杂度：O(L)，其中 L 是链表的长度。

• 空间复杂度：O(L)，其中 L是链表的长度。主要为栈的开销。

那有没有一种方法既能用一次循环代替两次循环，而且空间复杂度还不会提高呢？

转念一想，上面黑体字不正是双指针法解决的问题吗？

第三种方法：双指针法

（1）定义fast指针和slow指针，初始值为虚拟头结点.

（2）fast首先走n + 1步 ，为什么是n+1呢，因为只有这样同时移动的时候slow才能指向删除节点的上一个节点。

（3）fast和slow同时移动，直到fast指向末尾

（4）删除slow指向的下一个节点

现在有一个问题，为什么fast先走n+1步之后二者同时移动，slow恰好指向倒数第n个节点的前一个节点？（由于本题删除节点的需要，我们需要找到被删除节点的前一个结点）

换句话说，为什么fast先走n步之后二者同时移动，slow恰好指向倒数第n个节点？

说下我的理解：fast移动n步之后，fast与slow之间距离之差为n个节点，由于两个指针移动速度相同，在移动次数相同的情况下，二者的距离差是一定的，因此当fast指向NULL时，slow与fast的距离差仍然是n，而根据“倒数”这一定义，slow指向的地方这不恰恰是倒数第n个节点吗？

如果仍不太理解，可以看这里

代码如下：

class Solution {
public:
    ListNode* removeNthFromEnd(ListNode* head, int n) {
        ListNode* dummyHead = new ListNode(0, head);
        ListNode* fast = dummyHead;
        ListNode* slow = dummyHead;
        while (n-- && fast != nullptr) {
            fast = fast->next;
        }
        //再让fast走一步
        fast = fast->next;
        // fast和slow一起走，二者之间距离差不变
        //因此fast指向NULL时slow指向倒数第n个节点的前一个节点
        while (fast != nullptr) {
            fast = fast->next;
            slow = slow->next;
        }
        ListNode* temp = slow->next; //保存该节点便于释放内存
        slow->next = slow->next->next;
        delete temp;
        return dummyHead->next;
    }
};

• 时间复杂度：O(L)，其中 L 是链表的长度。
• 空间复杂度: O(1)

Leetcode 160.链表相交

题目链接：Leetcode 160.链表相交

题目描述：给你两个单链表的头节点 headA 和 headB ，请你找出并返回两个单链表相交的起始节点。如果两个链表没有交点，返回 null 。

思路：

PS：这道题真的被leetcode大佬的题解折服了，以至于其他方法黯然失色（就是表达一下心情，没有说其他方法不好的意思）同样是双指针，但是思路非常巧妙，写法非常简洁！！！

注：以下思路及证明过程来自于Leetcode题解区：

160. 相交链表 - 力扣（LeetCode）

（1）首先判断两个链表是否为空，如果为空，则一定没有交点。

（2）当二者均不为空时，创建两个指针pA，pB分别指向两个链表的头节点,然后将两个指针依次遍历两个链表的每个节点。具体步骤如下：

• 每步操作需要同时更新指针 pA 和 pB。
• 如果指针 pA 不为空，则将指针 pA 移到下一个节点；如果指针 pB 不为空，则将指针 pB移到下一个节点。

• 如果指针 pA 为空，则将指针 pA移到链表 headB 的头节点；如果指针 pB 为空，则将指针 pB 移到链表 headA 的头节点。

• 当指针 pA 和 pB 指向同一个节点或者都为空时，返回它们指向的节点或者 nullptr。

对于双指针方法的证明过程如下：

以下是代码：

class Solution {
public:
    ListNode* getIntersectionNode(ListNode* headA, ListNode* headB) {
        if (headA == nullptr || headB == nullptr) {
            return nullptr;
        }
        ListNode *pA = headA, *pB = headB;
        while (pA != pB) {
            pA = pA == nullptr ? headB : pA->next;
            pB = pB == nullptr ? headA : pB->next;
        }
        return pA;
    }
};

• 时间复杂度：时间复杂度：O(m+n))，其中 m 和 n 是分别是链表 headA 和 headB 的长度。两个指针同时遍历两个链表，每个指针遍历两个链表各一次。
• 空间复杂度: O(1)。

Leetcode 142.环形链表II

题目链接：Leetcode 142.环形链表II

题目描述： 给定一个链表，返回链表开始入环的第一个节点。 如果链表无环，则返回 null。

思路：本题通过数学推导出一个小结论，并根据双指针法实现。主要分为两个步骤：

• 判断链表是否环
• 如果有环，如何找到这个环的入口

判断是否有环很简单，假设快指针一次移动两个节点，慢指针一次移动一个节点，直到快指针移动到NULL。

（1）如果无环，则快慢指针不会相遇。

第一个很好理解，快指针移动的快，慢指针肯定追不上

（2）如果有环，则快慢指针会相遇，且会在环内相遇。

第二个需要大家思考一下，首先快慢指针在环里相遇，为什么？由于快指针速度快，会先一步进入环，一直绕环旋转而不会出环，直到慢指针进入环。那为什么一定会相遇呢，不会出现快指针越过慢指针的情况吗？答案是不会。因为二者速度之差仅为1个节点，换句话说，快指针在慢指针进入环内以1个节点的速度接近慢指针，因此一定会相遇。

判断是否有环之后，通过一定的数学推导可以巧妙的实现第二个问题（至于怎么想到的我也不知道，也许是某位大佬灵光一动就推出来了）。具体的推导过程看这里

代码实现：

class Solution {
public:
    ListNode* detectCycle(ListNode* head) {
        ListNode* fast = head;
        ListNode* slow = head;
        while (fast != nullptr && fast->next != nullptr) {
            fast = fast->next->next;
            slow = slow->next;
            // 快慢指针相遇，此时从head 和 相遇点，同时查找直至相遇
            if (fast == slow) {
                ListNode* index1 = fast;
                ListNode* index2 = head;
                while (index1 != index2) {
                    index1 = index1->next;
                    index2 = index2->next;
                }
                return index2;// 返回环的入口
            }
        }
        return nullptr;
    }
};

• 时间复杂度: O(n)，快慢指针相遇前，指针走的次数小于链表长度，快慢指针相遇后，两个index指针走的次数也小于链表长度，总体为走的次数小于 2n
• 空间复杂度: O(1)

总结：作为初学者，学习前人的经验是必要的，今天的第三题和第四题就是很好的例子，一开始我只能想出最简单的方法，但是通过理解其他人的方法，我也感觉到有很大的长进。

最后，如果文章有错误，请在评论区或私信指出，让我们共同进步！