DIFFUSION POSTERIOR SAMPLING FOR GENERAL NOISY INVERSE PROBLEMS

Abstract

在最近的研究中，扩散模型被作为强大的生成逆问题求解器，因其高质量的重建和结合现有迭代求解器的便利性。然而，大多数研究侧重于在无噪声设置中解决简单的线性逆问题，这在很大程度上低估了真实世界问题的复杂性。在这项工作中，我们通过后验采样的逼近，将扩散求解器有效地扩展到处理一般的带噪声（非）线性逆问题。有趣的是，所得到的后验采样方案是扩散采样与流形约束梯度的混合版本，而无需严格的测量一致性投影步骤，在噪声环境中相比先前的研究具有更理想的生成路径。我们的方法表明，扩散模型可以整合各种测量噪声统计，如高斯和泊松，同时有效处理噪声的非线性逆问题，如傅立叶相位恢复和不均匀的去模糊。

1. Introduction

扩散模型通过匹配对数密度的梯度来学习底层数据分布的隐式先验，即，${\nabla }_{x}logp(x)$ 。先验信息在解逆问题时可以发挥作用，这些逆问题旨在通过前向测量算子 $\mathcal{A}$ 和探测器噪声 $n$ 相关联的测量 $y$ 来恢复 $x$。当我们知道这样的前向模型时，我们可以加入对数似然的梯度（即 ${\nabla }_{x}logp(y|x)$)，以便从后验分布$p(x|y)$中抽样。虽然这看起来很简单，但实际上，由于扩散模型依赖于时间$t$，似然项在解析上是棘手的。由于其难以处理，人们通常转而将其投影到测量子空间上。然而，在以下两种情况下，投影型方法会出现显著失败：1) 当测量中存在噪声时，由于逆问题的病态性，在生成过程中通常会放大噪声；2) 测量过程是非线性的。

其中一个旨在解决噪声逆问题的工作是在谱域中运行扩散（Kawar et al.，2021；2022），从而可以通过奇异值分解将测量域中的噪声绑定到谱域中。尽管如此，当前向模型变得更加复杂时，SVD 的计算是昂贵的，甚至是不可行的。例如，Kawar等人（2022）只考虑了可分离的高斯核来进行去模糊，因为它们被限制在可以有效地执行SVD的逆问题家族中，因此，这些方法的适用性受到限制，因此设计一种在不需要计算奇异值分解的情况下解决带噪声逆问题的方法将会非常有用。此外，当扩散模型被应用于各种逆问题时包括图像修复，超分，着色等问题，据我们所知，到目前为止，所有的工作都只考虑线性逆问题，而没有探索非线性逆问题。

在这项工作中，我们设计了一种绕过扩散模型后验采样难以处理的方法，通过一种新颖的逼近，该方法通常适用于带噪声的逆问题。具体而言，我们展示了我们的方法可以高效处理高斯和泊松测量噪声。此外，当梯度可以通过自动微分获得时，我们的框架轻松扩展到任何非线性逆问题。我们进一步揭示了最近提出的流形约束梯度（Manifold Constrained Gradients，MCG）方法（Chung等，2022a）是所提出的方法在测量无噪声时的一种特殊情况。通过几何解释，我们进一步展示了与先前的方法（Chung等，2022a）相比，所提出的方法在噪声环境中更有可能产生理想的采样路径。此外，所提出的方法完全在图像域而非频谱域上运行，因此避免了为实现高效计算而进行奇异值分解。通过包括修复、超分辨率、（高斯/运动/非均匀）去模糊、傅立叶相位恢复等多种逆问题的广泛实验证明，我们的方法作为解决一般带噪声逆问题的通用框架，具有优越的质量（图1中显示了代表性结果）。

2. Background

2.1 SCORE-BASED DIFFUSION MODELS

扩散模型将生成过程定义为噪声过程的逆过程，具体而言，Song等人（2021b）为数据加噪过程（即正向随机微分方程 SDE）$x(t)$，其中 $t\in [0,T],x(t)\in R^d$ 对应的随机微分方程（SDE）定义如下：

$$dx=-\frac{\beta (t)}{2}xdt+\sqrt{\beta (t)}dw\text{\hspace{1em}(1)}$$

其中，$\beta (t):\mathbb{R}\to \mathbb{R}>0$是该过程的噪声进程，通常被取为关于t 的单调递增线性函数。其中，$w$ 是标准的$d$维维纳过程（Wiener process）。数据分布在 t = 0时定义，即 $x(0)\sim p_{\text{data}}$，而在 $t=T$ 时，即 $x(T)\sim \mathcal{N}(0,I)$，是一个简单且易处理的分布（例如各向同性高斯分布）。

维纳过程（Wiener process），也称为布朗运动（Brownian motion），是一种随机过程。
维纳过程具有以下特性：

1. 连续性： 维纳过程是一个连续的随机过程，即其轨迹在任意时间点处是连续的。
2. 马尔可夫性： 在给定现在的情况下，未来的演变是与过去的演变独立的，即满足马尔可夫性质。
3. 独立增量： 维纳过程的增量在不同的时间段上是独立的。这意味着在任意一段时间内，过程的变化不受之前的变化的影响。
4. 高斯性： 维纳过程在任意固定的时间点上的取值是正态分布的。
5. 零均值： 维纳过程的期望增量是零。

我们的目标是从可处理的分布开始恢复数据生成的分布，这可以通过写下相应的反向SDE来实现
$$dx=[-\frac{\beta (t)}{2}x-\beta (t){\nabla }_{x_t}\log p_t(x_t)]dt+\sqrt{\beta (t)}d\bar{w}\text{\hspace{1em}(2)}$$
其中，$dt$ 对应于时间倒流，$d\bar{w}$ 对应于标准 Wiener 过程的反向运行。漂移函数现在依赖于时间相关的得分函数${\nabla }_{x_t}\log p_t(x_t)$，该函数由一个经过训练的神经网络 $s_{\theta }$ 近似，该神经网络通过去噪得分匹配进行训练。

式子 (3) 中定义了优化问题，其中 ${\theta }^{\ast }$ 是使得损失最小化的参数，具体形式如下：

$${\theta }^{\ast }=\arg \underset{\theta }{\min }{\mathbb{E}}_{t\sim U(ϵ,1),x(t)\sim p(x(t)|x(0)),x(0)\sim p_{\text{data}}}{\Vert s_{\theta }(x(t),t)-{\nabla }_{x_t}\log p(x(t)|x(0))\Vert }_2^2\text{\hspace{1em}(3)}$$

其中，$ϵ\approx 0$ 。一旦通过 (3) 获得了 ${\theta }^{\ast }$，可以使用近似值 ${\nabla }_{x_t}\log p_t(x_t)\approx s_{{\theta }^{\ast }}(x_t,t)$ 作为 (2) 中得分函数的替代估计。对 (2) 进行离散化并使用例如 Euler-Maruyama 离散化进行求解，相当于从数据分布 $p(x)$ 中进行采样，这是生成建模的目标。

在整篇论文中，我们采用标准的 VP-SDE（即 Dhariwal 和 Nichol（2021）的 ADM 或 Denoising Diffusion Probabilistic Models（DDPM）（Ho 等，2020））。其中，我们用$\tilde{\sigma }(t)$ 表示的反向扩散方差，按照 Dhariwal 和 Nichol（2021）的方法学习得到的。在离散设置中（例如在算法中），使用 N 个划分，我们定义：
$x_i\triangleq x(tT/N)$，${\beta }_i\triangleq \beta (tT/N)$。随后，按照 Ho 等人（2020）的定义：${\alpha }_i\triangleq 1-{\beta }_i$，${\bar{\alpha }}_i\triangleq {\prod }_{i=1}^n{\alpha }_i$。

2.2 INVERSE PROBLEM SOLVING WITH DIFFUSION MODELS

对于各种科学问题，我们有一个由 x 导出的部分测量 y。当映射 $x\mapsto y$ 是多对一的情况下，我们面临一个逆问题，即我们无法精确地恢复 x。在贝叶斯框架中，人们使用 $p(x)$ 作为先验，并从后验分布 $p(x|y)$ 中采样，其中这种关系在贝叶斯框架中被正式建立为：$p(x|y)=\frac{p(y|x)p(x)}{p(y)}$ 利用扩散模型作为先验，可以直接修改 (2) 来得到从后验分布采样的逆扩散采样器：
$$dx=[-\frac{\beta (t)}{2}x-\beta (t)\left({\nabla }_{x_t}\log p_t(x_t)+{\nabla }_{x_t}\log p_t(y|x_t)\right)]dt+\sqrt{\beta (t)}d\bar{w}\text{\hspace{1em}(4)}$$
其中：
$${\nabla }_{x_t}\log p_t(x_t|y)={\nabla }_{x_t}\log p_t(x_t)+{\nabla }_{x_t}\log p_t(y|x_t)\text{\hspace{1em}(5)}$$

在公式 (4) 中，有两个需要计算的项：得分函数 ${\nabla }_{x_t}\log p_t(x_t)$ 和似然函数 ${\nabla }_{x_t}\log p_t(y|x_t)$。为了计算涉及 $p_t(x)$ 的前者，我们可以直接使用预训练的得分函数 $s_{{\theta }^{\ast }}$。然而，由于后者依赖于时间 $t$，其形式难以获得闭合解，因为只有 y 和$x_0$之间存在显式的依赖关系。

在形式上，正向模型的一般形式可以表述为：
$$y=\mathcal{A}(x_0)+n,y,n\in {\mathbb{R}}^n,x\in {\mathbb{R}}^d\text{\hspace{1em}(6)}$$
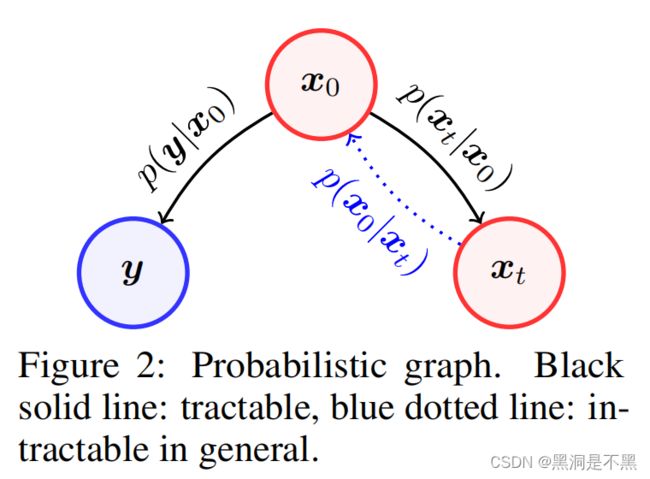
其中，$\mathcal{A}(\cdot ):{\mathbb{R}}^d\to {\mathbb{R}}^n$ 是正向测量算子，$n$ 是测量噪声。在白噪声高斯噪声的情况下，$n\sim \mathcal{N}(0,{\sigma }^{2}I)$。在明确的形式中，$p(y|x_0)\sim \mathcal{N}(y|\mathcal{A}(x_0),{\sigma }^{2}I)$。然而，如图 2 的概率图中所示，在 $y$ 和 $x_t$ 之间不存在明确的依赖关系，即蓝色虚线保持未知。

为了规避直接使用似然项，交替投影到测量子空间是一种广泛使用的策略（Song 等，2021b；Chung & Ye，2022；Chung 等，2022b）。换句话说，可以忽略 (4) 中的似然项，首先使用 (2) 进行无条件更新，然后采取投影步骤，以确保测量一致性得到满足，假设 $n\approx 0$。另一方面，另一项工作（Jalal 等，2021）解决了 $A(x)\approx Ax$ 的线性逆问题，并利用近似值 ${\nabla }_{x_t}\log p_t(y|x)\approx \frac{AH(y-Ax)}{{\sigma }^2}$，其中假设 $n$ 是方差为 ${\sigma }^2$ 的高斯噪声。然而，该方程仅在 $t=0$ 时正确，而在实际生成过程中使用的所有其他噪声水平上都是错误的。通过启发式方法，通过假设噪声水平随着 $t\to T$ 的增加而增加，以抵消不正确性，即 ${\nabla }_{x_t}\log p_t(y|x)\approx \frac{AH(y-Ax)}{{\sigma }^2+{\gamma }^{2}t}$，其中 $\{{\gamma }_t{\}}_{t=1}^T$ 是超参数。虽然这两条研究线路都旨在在给定测量的情况下执行后验采样，并在无噪声逆问题上在经验上表现良好，但需要注意的是：1）它们不提供处理测量噪声的手段，2）使用这些方法来解决非线性逆问题要么无法正常工作，要么不容易实现。本文的目标是迈向更通用的逆问题求解器，旨在处理带有噪声的测量，并能够有效扩展到非线性逆问题。

3 DIFFUSION POSTERIOR SAMPLING (DPS)

3.1 APPROXIMATION OF THE LIKELIHOOD

回忆一下，对于 $p(y|xt)$ 不存在解析公式。
为了利用观测模型 $p(y|x_0)$，我们将 $p(y|xt)$ 进行了分解，如下所示：
$$\begin{gathered} p(y|x_t)=\int p(y|x_0,x_t)p(x_0|x_t)d{x}_0 \\ =\int p(y|x_0)p(x_0|x_t)d{x}_0\text{\hspace{1em}(7)} \end{gathered}$$

第二个等式来自于在图 2 中显示的 $y$ 和 $x_t$ 对 $x_0$ 条件独立。在这里，$p(x_0|x_t)$，如图 2 中的蓝色虚线所示，通常是难以处理的。但是，对于扩散模型（如 VP-SDE 或 DDPM），正向扩散可以简单地表示为
$$x_t=\sqrt{\bar{\alpha }(t)}{x}_0+\sqrt{1-\bar{\alpha }(t)}z,z\sim \mathcal{N}(0,I)\text{\hspace{1em}(8)}$$

这样，我们可以通过 Tweedie 方法（Efron, 2011; Kim & Ye, 2021）获得后验均值的表示，如 Proposition 1 所示。

事实上，该结果与已经建立的去噪领域密切相关。具体而言，考虑从给定的高斯噪声 $x_t$ 中恢复干净的 $x_0$ 的估计问题。Tweedie 公式的一个经典结果（Robbins, 1992; Stein, 1981; Efron, 2011; Kim & Ye, 2021）表明，可以使用 (10) 中的公式检索经验贝叶斯最优的后验均值 ${\hat{x}}_0$。

鉴于可以在中间步骤高效计算的后验均值 ${\hat{x}}_0$，我们为 $p(y|x_t)$ 提供一个可处理的近似，以便可以使用替代函数最大化似然性，从而得到近似的后验采样。具体来说，鉴于 $p(y|x_t)={\mathbb{E}}_{x_0\sim p(x_0|x_t)}[p(y|x_0)]$（公式 (7)），我们使用以下近似：
$$p(y|x_t)\approx p(y|{\hat{x}}_0)$$
其中 $${\hat{x}}_0:=\mathbb{E}[x_0|x_t]={\mathbb{E}}_{x_0\sim p(x_0|x_t)}[x_0]\text{\hspace{1em}(11)}$$意味着在后验分布上对 $p(y|x_0)$ 的外部期望被替换为对 $x_0$ 的内部期望。实际上，这种类型的近似与 Jensen 不等式密切相关，因此我们需要以下定义来量化近似误差：

以下定理推导了当 $n\sim \mathcal{N}(0,{\sigma }^{2}I)$ 时，从 (6) 推导出逆问题的 Jensen 不等式的闭式上界：

Remark 2. 在大多数逆问题中，$||{\nabla }_x\mathcal{A}(x)\Vert$ 是有限的。这不应与逆问题的病态性混淆，病态性指的是逆算子 ${\mathcal{A}}^{-1}$ 的无界性。因此，如果 $m_1$ 也是有限的（这在实践中是大多数分布的情况），则定理1中的 Jensen 差可以在 $\sigma \to \infty$ 时趋近于 0，这表明随着测量噪声的增加，近似误差减小。这可能解释了为什么我们的 DPS 在嘈杂的逆问题中效果良好。此外，尽管我们已经指定测量分布为高斯分布，但我们也可以以类似的方式确定其他测量分布（例如泊松分布）的 Jensen 差。
通过利用定理1的结果，我们可以使用对数似然的近似梯度 $${\nabla }_{x_t}\log p_t(y|x_t)\approx {\nabla }_{x_t}\log p_t(y|{\hat{x}}_0)\text{\hspace{1em}(15)}$$其中后者现在是解析可处理的，因为测量分布是已知的。

3.2 MODEL DEPENDENT LIKELIHOOD OF THE MEASUREMENT

请注意，我们可能对每个应用程序有不同的测量模型$p(y|x_0)$。反问题中最常见的两种情况是高斯噪声和泊松噪声。在这里，我们探讨了如何将上述描述的扩散后验采样方法适应到每种情况。

Gaussian noise.
似然函数的形式为
$$p(y|x_0)=\frac{1}{(2\pi {)}^{n/2}{\sigma }^{2n}}\exp \left(-\frac{\Vert y-A(x_0){\Vert }_2^2}{2{\sigma }^2}\right)$$
其中 $n$ 表示测量 $y$ 的维度。通过对 $p(y|x_t)$ 关于 $x_t$ 求导，利用定理1 和 (15)，我们得到$${\nabla }_{x_t}\log p_t(y|x_t)\approx -\frac{1}{{\sigma }^2}{\nabla }_{x_t}\Vert y-A({\hat{x}}_0(x_t)){\Vert }_2^2,$$其中我们明确地表示 ${\hat{x}}_0:={\hat{x}}_0(x_t)$，以强调 ${\hat{x}}_0$ 是 $x_t$ 的函数。因此，计算梯度 ${\nabla }_{x_t}$ 相当于通过网络进行反向传播。

将定理1 的结果代入到 (5) 中，使用训练好的得分函数，我们最终得出
$${\nabla }_{x_t}\log p_t(x_t|y)\approx s_{{\theta }^{\ast }}(x_t,t)-\rho {\nabla }_{x_t}\Vert y-\mathcal{A}({\hat{x}}_0){\Vert }_2^2\text{\hspace{1em}(16)}$$ 其中 $\rho =1/{\sigma }^2$被设置为步长。

Poisson noise. 对于 Poisson 测量下的似然函数，在独立同分布的假设下
$$p(y|x_0)\to \prod _{j=1}^n\frac{{\left[A(x_0)\right]}_j^{y_j}}{y_j!}\exp \left[-\mathcal{A}(x_0{)}_j\right]\text{\hspace{1em}(17)}$$
其中 $j$ 是测量箱的索引。在大多数情况下，如果测量值不太小，该模型可以用高斯分布极高的准确度进行近似。即，
$$p(y|x_0)\to \prod _{j=1}^n\frac{1}{\sqrt{2\pi {\left[\mathcal{A}(x_0)\right]}_j}}\exp \left(-\frac{(y_j-[\mathcal{A}(x_0){]}_j{)}^2}{2{\left[\mathcal{A}(x_0)\right]}_j}\right)\text{\hspace{1em}(18)}$$ $$\simeq \prod _{j=1}^n\frac{1}{\sqrt{2\pi y_j}}\exp \left(-\frac{(y_j-[\mathcal{A}(x_0){]}_j{)}^2}{2y_j}\right)\text{\hspace{1em}(19)}$$
其中我们使用了标准的射击噪声模型的近似 $[A(x_0){]}_j\approx y_j$ 来得到最后一个方程（Kingston, 2013）。然后，类似于高斯情况，通过微分和定理1的使用，我们得到
$${\nabla }_{x_t}\log p_t(y|x_t)\simeq -\rho {\nabla }_{x_t}\Vert y-A(x_0){\Vert }_2^2,[\Lambda {]}_{ii}=\frac{1}{2y_j}\text{\hspace{1em}(19)}$$其中 $||a|{|}_{\Lambda }^2\equiv a^T\Lambda a$，我们已经包括了$\rho$ 来定义步长，就像在高斯情况下一样。我们可以总结我们对每个噪声模型的策略如下：
$${\nabla }_{x_t}\log p_t(x_t|y)\simeq s_{{\theta }^{\ast }}(x_t,t)-\rho {\nabla }_{x}t\Vert y-A({\hat{x}}_0){\Vert }_2^2\text{(Gaussion)}\text{\hspace{1em}(21)}$$$${\nabla }_{x_t}\log p_t(x_t|y)\simeq s_{{\theta }^{\ast }}(x_t,t)-\rho {\nabla }_{x_t}\Vert y-A({\hat{x}}_0){\Vert }_{\Lambda }^2,[\Lambda {]}_{ii}=\frac{1}{2y_j}\text{(Poisson)}\text{\hspace{1em}(22)}$$将 (16) 或 (21) 结合到通常的ancestral sampling 步骤（Ho et al., 2020）中得到算法1 2。我们将我们的算法命名为扩散后验采样（Diffusion Posterior Sampling，DPS），因为我们构建了我们的方法以从后验分布中进行采样。请注意，与以前的方法不同，它们仅限于线性逆问题 $\mathcal{A}(x)=Ax$，我们的方法是完全通用的，我们还可以使用非线性算子 $\mathcal{A}(\cdot )$。为了证明这确实是这种情况，在实验部分我们选择两个非常困难的非线性逆问题：Fourier 相位恢复和非均匀去模糊，并展示我们的方法即使在这些具有挑战性的问题设置中也具有非常强大的性能。

Geometry of DPS and connection to manifold constrained gradient (MCG). 有趣的是，在高斯测量情况下，我们的方法对应于 Chung 等人（2022a）中提出的流形约束梯度（Manifold Constrained Gradient，MCG）步骤，当从 Chung 等人（2022a）中设置 $W=I$ 时。

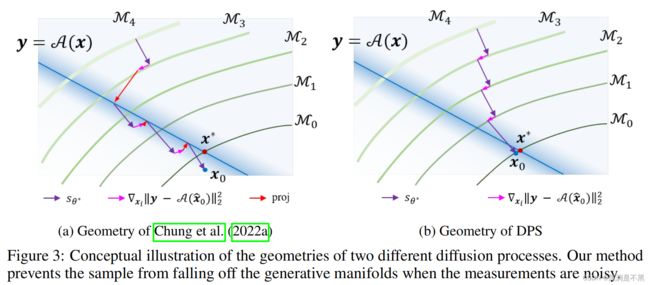
然而，Chung 等人（2022a）在通过（16）进行更新步骤之后另外执行了对测量子空间的投影，可以将其看作是对偏离完美数据一致性的修正。借用从 Chung 等人（2022a）那里对扩散模型的解释，我们在几何上比较了生成过程。在扩散模型的背景下，通过 $s_{{\theta }^{\ast }}$ 进行的单一去噪步骤对应于对数据流形的正交投影，并且梯度步骤 ${\nabla }_{x_i}\Vert y-\mathcal{A}({\hat{x}}_0){\Vert }_2^2$ 采取了切向当前流形的步骤。对于嘈杂的逆问题，当像 Chung 等人（2022a）那样在每个梯度步骤之后对测量子空间进行投影时，由于过于施加仅适用于无噪声测量的数据一致性，样本可能会偏离流形，积累误差，并且到达错误的解决方案，如图3a所示。另一方面，我们的方法没有对测量子空间进行投影，因此不受嘈杂测量的这些缺点的影响（见图3b）。因此，尽管测量子空间上的投影对于 Chung 等人（2022a）试图解决的无噪声逆问题是有用的，但它们在我们试图解决的嘈杂逆问题中却失败得很严重。最后，当与测量子空间上的投影步骤一起使用时，MCG 表明为不同的应用选择不同的 $W$ 是必要的，而我们的方法不受这样的启发法的限制。

4 EXPERIMENTS

Experimental setup.

我们在两个具有不同特征的数据集上测试了我们的实验—FFHQ 256×256（Karras等人，2019）和 Imagenet 256×256（Deng等人，2009），分别在1k个验证图像上。经过预先训练的 ImageNet的扩散模型取自达里瓦尔和尼科尔（2021年），并直接使用，无需对特定任务进行微调。采用49k 训练数据从头开始训练FFHQ的扩散模型 (to exclude 1k validation set) for 1M steps。所有的图像都被归一化到范围[0,1]。前向测量操作符指定如下： (i) For box-type inpainting,，我们根据Chung等人（2022a）掩盖了128×128矩形区域，对于随机类型，我们屏蔽了92%的总像素（所有RGB通道）。（ii）对于超分辨率，进行双边降采样。(iii) Gaussia n模糊核的大小为61×61，标准偏差为3.0，运动模糊用代码6随机生成，大小为61×61，强度值为0.5。玉米粒与地面进行卷积 真实图像产生测量。（iv）对于相位检索，对图像进行傅里叶变换，只取傅里叶幅度作为测量。(v)对于非线性去模糊处理 ，我们利用Tran等人（2021）中的神经网络近似正向模型。所有高斯噪声添加到测量域，σ = 0.05。泊松噪声水平设置为λ = 1.0。

我们对以下方法进行了比较：去噪扩散恢复模型（DDRM）（Kawar等，2022）、流形约束梯度（MCG）（Chung等，2022a）、即插即用交替方向乘子法（PnP-ADMM）（Chan等，2016，其中使用了DnCNN Zhang等，2017，代替近端映射）、总变差（TV）稀疏正则化优化方法（ADMM-TV），以及Score-SDE（Song等，2021b）。请注意，Song等（2021b）仅提出了一种用于修补的方法，而不是用于一般的逆问题。然而，通过在迭代潜变量细化（ILVR）（Choi等，2021）中以相同方式应用投影到凸集的迭代方法（POCS），以及更一般地应用于线性逆问题（Chung等，2022b），Score-SDE的方法被用于超分辨率，因此我们简称这些方法为Score-SDE。为了公平比较，我们对所有基于扩散的不同方法（即DPS、DDRM、MCG、Score-SDE）使用了相同的评分函数。

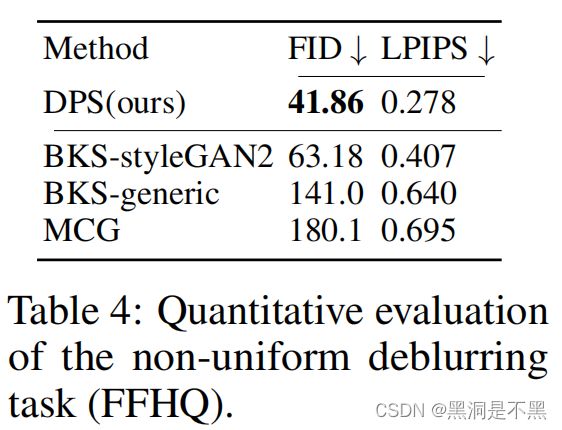
相位恢复方面，我们与三个被视为标准的强基线进行比较：过采样平滑（OSS）（Rodriguez等，2013）、混合输入输出（HIO）（Fienup和Dainty，1987）和误差减小（ER）算法（Fienup，1982）。对于非线性去模糊，我们与先前的方法进行比较：模糊核空间（BKS）- StyleGAN2（Tran等，2021），基于GAN先验；模糊核空间（BKS）- 通用（Tran等，2021），基于超拉普拉斯先验；以及MCG。附录D提供了更多实验细节。对于定量比较，我们关注以下两个广泛使用的感知指标：Fréchet Inception Distance（FID）和学习的感知图像块相似度（LPIPS）距离，并在附录E中提供了进一步评估的标准指标：峰值信噪比（PSNR）和结构相似性指数（SSIM）。

Noisy linear inverse problems.

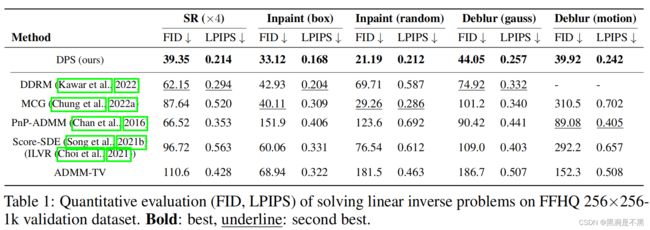
我们首先在具有高斯测量噪声的各种线性逆问题上测试我们的方法。表1、2中的定量结果表明，所提出的方法在性能上明显优于所有其他比较方法。特别是，依赖于测量子空间投影的MCG和Score-SDE（或ILVR）是方法，其中生成过程受控以确保测量一致性完美满足。虽然这对于无噪声（或可以忽略的噪声）的问题很有用，在我们不能忽视噪声的情况下，解决方案会过度拟合到受损的测量值（有关更多讨论，请参见附录C.1）。在图4中，我们特别将我们的方法与DDRM和PnP-ADMM进行比较，这是两种已知对测量噪声具有鲁棒性的方法。我们的方法能够在所有任务上提供清晰而逼真的高质量重建。另一方面，我们发现DDRM在图像修复任务中表现不佳，其中测量的维度非常低，并且在SR和去模糊任务上产生更模糊的结果。我们进一步指出，DDRM依赖于奇异值分解（SVD），因此仅能解决前向测量矩阵可以有效实现的问题（例如，在去模糊的情况下是可分离的核）。因此，虽然可以解决高斯模糊问题，但不能解决诸如运动去模糊之类的问题，其中点扩散函数（PSF）更复杂。相反，我们的方法不受此类条件限制，可以始终使用，而不受复杂性的限制。Poisson噪声线性逆问题的结果如图5所示。与高斯情况一致，DPS能够生成与地面实况紧密模拟的高质量重建。从实验中，我们进一步观察到在算法2中采用的加权最小二乘法相对于其他可能用于Poisson逆问题的选择而言效果最好（有关进一步分析，请参见附录C.4）。

Nonlinear inverse problems.

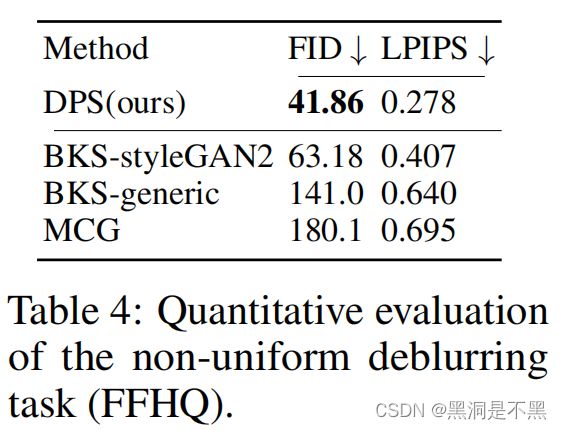
我们在表3 中展示了相位恢复的定量结果，表4中展示了非线性去模糊的结果。图6展示了代表性的结果。我们首先观察到，所提出的方法能够对给定的相位恢复问题进行高度准确的重建，捕捉大部分高频细节。然而，我们还观察到并非总是能够获得高质量的重建。实际上，由于相位恢复在某些条件下存在非唯一性，广泛使用的方法如HIO也依赖于初始化（Fienup，1978），因此通常是先生成多个重建样本，然后选择最佳样本进行报告。因此，在报告我们的定量指标时，我们为所有方法生成4个不同的样本，并基于最佳样本报告指标。我们看到DPS在很大程度上优于其他方法。对于非线性去模糊的情况，我们再次看到我们的方法表现最佳，产生高度逼真的样本。BKS-styleGAN2（Tran等，2021）利用了GAN先验，因此生成了可行的人脸，但严重扭曲了身份。BKS-generic利用了Hyper-Laplacian先验（Krishnan和Fergus，2009），但不能正确去除伪影和噪声。MCG以与图7中讨论的类似的方式放大噪声。