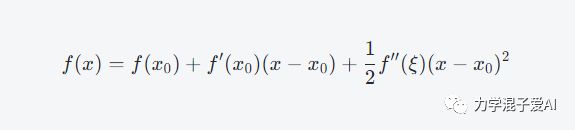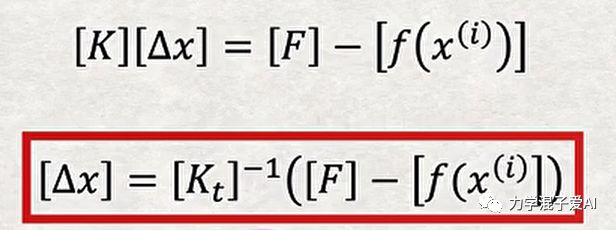有限元非线性求解算法——Newton-Raphson

0. 前言

有限元静力问题的求解实际上最终通过某些理论方法（最小势能原理，虚功原理，加权残值法等）转化为 K(u)u=F 形式的矩阵方程（非线性方程或者方程组）的求解，这里K是全局刚度矩阵，通过力学三大方程和试函数求得；u是节点位移向量，是待求的未知数，其中可以通过位移边界条件减少未知数数量；F是节点荷载向量，是由荷载边界条件依据静力等效转化为节点荷载向量。因此求解非线性方程组，研究求解算法是一个难点，求解算法主要为增量法和迭代法，实际上真正有限元求解时是两种方法结合使用的。

1.算法来源

Newton-Raphson(牛顿-拉夫森)迭代法是一种求解方程根的常用方法。它使用函数的一阶和二阶导数信息来高效地逐步逼近方程根。

​

略去高阶项，整理可得到下式

需要注意的是，牛顿-拉夫森迭代法并不总是收敛。如果函数f(x)在某些点上的一阶或二阶导数为0，或者在根周围有一定的震荡行为，都可能导致算法无法收敛。此外，如果初始点x0选取得离根过远，也可能会导致算法无法收敛。因此，在实际使用中，需要根据实际情况灵活选择初始点、步长和迭代精度等参数，以保证算法的准确性和可靠性。下面图中展示了算法的格式。

非线性方程

​

非线性方程组

​

​

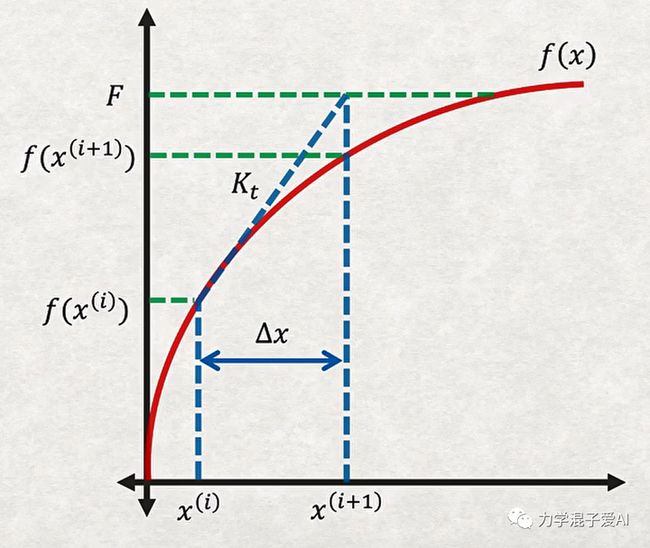
2. 非线性求解迭代过程

下面解释下有限元的求解非线性问题的迭代过程。上图是某个荷载增量步的求解示意图。

第一次迭代前，需要给一个位移初始值（假定的位移值），实际上位移初始值可以随便给，但是考虑到算法的实用性，收敛性和收敛速度，我们一般肯定希望初始值要么取值具有一般性或者接近真实位移值。一般初始位移值是通过当前荷载增量和初始刚度的比值来确定，在这里初始刚度就是当前增量开始时的刚度矩阵，荷载增量是人为设置的（有限元软件里面也可以设置，例如abaqus中设置如下图）

​ 荷载步内求解迭代过程

然后根据当前给定的位移值求出当前的刚度矩阵（记住刚度矩阵与材料属性和几何参数有关），并计算当前位移匹配的结构内力，接着计算内力与当然外载F的差值（也可以用位移容差控制，实际有限元中考虑荷载容差和位移容差），如果这个差值小于设置的容差，那么就停止迭代，否则继续重复上述步骤。

​

3.案例

(*Material Nonlinearity Example*)
Clear["Global`*"]
(*Parameters*)
L = 1.0;
A = 1;
p = X1^2;
(*Newton-Raphson Parameters*)
Xi = 1;
ErrorLimit = 0.5;
maxIter = 20;

(*Stress-Strain Relationship*)
s = 10*u'[X1] + 100000*u'[X1]^3;

(*Exact solution*)
DE = D[s*A, X1] + p;
sol = NDSolve[{DE == 0, u[0] == 0, u[L] == 0}, u[X1], X1];
uExact = u[X1] /. sol[[1]];
Plot[uExact, {X1, 0, L}];

(*RR Approximation，最小势能原理*)
(*此案例相当于三节点二次单元*)
(*Approximation Function*)
uApprox = a0 + a1*X1 + a2*X1^2;
(*Essential Boundary Conditions*)
BC1 = uApprox /. {X1 -> 0};
BC2 = uApprox /. {X1 -> L};
sol1 = Solve[{BC1 == 0, BC2 == 0}, {a0, a1}]; {a0, a1} = {a0, a1} /. 
  sol1[[1]];
uApprox;

(*Total Internal Strain Energy*)
S = 10*e + 100000*e^3;
SED = Integrate[S, {e, 0, e}];          (*单位体积应变能*)
e = D[uApprox, X1];
TSE = Integrate[SED, {X1, 0, L}];              (*总应变能*)

(*work*)
w = Integrate[p*uApprox, {X1, 0, L}];           (*外力功*)
(*Potential Energy*)
PE = TSE - 
   w    ;                                  (*偏导等于0，对应的方程组的解，即为代求*)

(*Newton-Raphson Method*)
ai = {a2};
Func = D[PE, a2] ;              (*我们要这个方程组的解,这里是解a2*)

Kt = D[Func, a2];

 {
 {For[i = 1, i <= maxIter, i++,
   
   (*calculate Function and Kt at currentIteration*)
   FuncIter = Func /. {a2 -> Xi};
   KtIter = Kt /. {a2 -> Xi};
   
   (*Solving for Delta x*)
   Delta = (-1)*FuncIter/KtIter;
   
   (*Finding xi for Next Iteration*)
   XInit = Xi;
   Xi = Xi + Delta;
   
   (*Break Loop Once Convergence 0ccurs*)
   Error = (Delta/XInit)*100;
   If[Abs[Error] <= ErrorLimit,
    Print["Analysis Converged ! "];
    Print[" Coefficient a2 = ", Xi]; Print["Error = ", Error, "(%)"];
    a2 = Xi;
    Conv = 1;
    Break[]];
   (*Track Results*)
   Print["Iteration: ", i];
   Print["coefficient a2 = ", Xi]; Print["Error = ", Error, "(%)"];
   (*Error Message if Max Number of IterationsReached*)If[i == maxIter,
    Print["Max of Number of Iterations Reached"]];
   ]},
 {\[Placeholder]}
} 
uApprox
Plot[{uExact, uApprox}, {X1, 0, L}, PlotLegends -> {"Exact" , "FEA"}, 
 AxesLabel -> {"Bar Length", "Displacement"}, AspectRatio -> 0.5]

下图显示了有限元解与精确解的沿着杆长的位移分布图，有一定的误差主要是这里为了简单起见，仅仅用了一个单元（三节点二次单元），想测试单元数量对结果精度的影响，可以将我的第一篇有限元笔记的代码和当前的结合起来修改下即可，这篇笔记旨在学习了解非线性有限元计算的的思路方法。

4. 结语

我一直都在分享笔记，是因为当前我也处于学习理论的状态，不过笔记较多，我分享的主要是之前一段时间的学习笔记，加上我当前的部分理解，重新整理呈现了出来。目前我在寻找损伤力学，断裂力学，张量分析，离散元等方面的优秀教材资料等，希望大家能分享给我，一起学习交流。​获取更多资料和学习交流欢迎大家关注公众号冬生亦东生，分享旨在本人复习和交流