算法------（1）区间合并

这个专栏的文章主要用来记录学习（复习）的算法。第一天先从区间合并开始。

例题：

解法是将所有区间按照左端点排序，然后从第一个区间开始依次遍历，如果该区间的左端点大于合现存合并区间的右端点，则将现存合并区间存入vector并将该区间作为新的现存合并区间，否则将两个区间合并作为新的现存合并区间。注意点有：（1）用fs和ed两个指针记录现存合并区间的作用端点，一开始赋为-2e9。（2）合并时是更新成两个区间右端点的最大值！！（3）最后还需要再进行一次存入操作。（4）对vector的排序需要用到迭代器，也就是.begin，.end。

#include 
#include 
#include 
using namespace std;
typedef pair PII;
void merge(vector &segs){
    vector res;
    int fs = -2e9,ed=-2e9;
    for(auto seg:segs){
        if(ed> k;
    vector segs;
    for(int i=0;i

例题：（1）

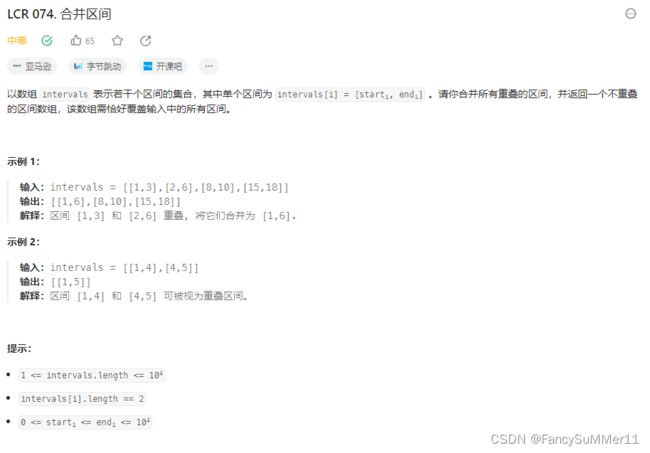
​​​​​LCR 074. 合并区间https://leetcode.cn/problems/SsGoHC/

模板题，套模板即可，注意判断是否为空集，注意不能再把st/ed赋值为-2e9，因为有个int的边界数据。。。。直接让st/ed为第一个区间的左右端点即可。

（2）也可以用区间合并的方式去思考。只不过这次合并时现存合并区间的右端点应该取ed和r两者最小，因为要求的是几个区间的共同交集而不是几个区间交集的并集。

class Solution {
public:
    int findMinArrowShots(vector>& points) {
        sort(points.begin(),points.end());
        int fs = (points[0])[0],ed = (points[0])[1],res = 0;
            for(auto seg:points){
                int l = seg[0],r = seg[1];
                if(ed

当然这么做并非最优解。最优解应该是将区间按照右端点排序。当我们考虑最少箭的时候，我们让任意一支箭向右移动，直到移动到这些气球内最靠左的右边界位置，此时所有气球仍然能爆炸且每一支箭都是在最靠左的右端点射出的。因此我们从具有最靠左的右端点的箭开始，排除每一个左端点小于这个右端点的箭，直到出现一个无法被打破的气球。此时这个无法被打破的气球相对后面区间的右端点一定是更小的，因此他就是下一个我们需要的右端点。更新右端点，箭数加一。

class Solution {
public:
    int findMinArrowShots(vector>& points) {
        sort(points.begin(),points.end(),[](const vector &u,const vector &v){
            return u[1]pos){
                res += 1;
                pos = seg[1];
            }
        }
        return res;
    }
};

(3)

用区间合并的方式去思考，有共同交集的几个区间只能留一个，因此就是第二个问题。只不过这次需要在有共同交集时累加答案，而在无交集时只要更新即可。

class Solution {
public:
    int eraseOverlapIntervals(vector>& intervals) {
        sort(intervals.begin(),intervals.end());
        int fs = -2e9,ed = -2e9,res = 0;
        for(auto seg:intervals){
            int l = seg[0],r = seg[1]; 
            if(ed<=l){
                fs = l;ed = r;
            }
            else{
                ed = min(ed,r);
                res+=1;
            }
        }
        return res;
    }
};

此时在考虑上面的第二种方法，需要注意的是第一个区间会被计算一次，因此结果初始化为-1。此时需要在当前区间左端点未超过右端点时res++。

class Solution {
public:
    int eraseOverlapIntervals(vector>& intervals) {
        sort(intervals.begin(),intervals.end(),[](const vector &u,const vector &v){
            return u[1]=pos){
                pos = seg[1];
            }
            else{
                res++;
            }
        }
        return res;
    }
};

其实还可以利用dp来做，用f（i）表示前i个区间里能选出的最大的不重复区间数，则可以分为倒数第二个选第1个区间，第2个区间。。。第i-1个区间，只要这些区间不跟第i个区间有交集，那么f（i）就是这些区间f的最大值+1。但是超时。（注意，一开始是每个都只选自己，因此每一个i的值都是1。）max_element可以求vector的最大值，返回迭代器。在用下标访问vector前需要给vector分配内存。否则报错。可以用二分进行优化，但是不是今天重点，后面复习dp再说吧。

class Solution {
public:
    int eraseOverlapIntervals(vector>& intervals) {
        if(intervals.empty()) {
            return 0;
        }
        int n = intervals.size();
        sort(intervals.begin(),intervals.end());
        vector x(n,1);
        for(int i = 1;i= intervals[j][1]) x[i] = max(x[j]+1,x[i]);
            }
        }
        return n - *max_element(x.begin(),x.end());
    }
};