【2025暑期实习冲刺】day02: 有序数组的平方、长度最小的子数组、螺旋矩阵
原题目链接
977.有序数组的平方
209. 长度最小的子数组
59. 螺旋矩阵 II
文章目录
- 977.有序数组的平方
-
- 1.思路分析
- 2.代码
- 209.长度最小的子数组
-
- 1. 思路分析
- 2.代码
- 59. 螺旋矩阵 II
-
- 1.思路分析
- 2.代码
第二天了!不看题解就ac的感觉好快乐!!周末想做个chatgpt辅助leetcode刷题的模型,不知道有木有小伙伴感兴趣。
977.有序数组的平方
先看题目
给你一个按 非递减顺序 排序的整数数组 nums,返回 每个数字的平方 组成的新数组,要求也按 非递减顺序 排序。
示例 1:
输入:nums = [-4,-1,0,3,10]
输出:[0,1,9,16,100]
解释:平方后,数组变为 [16,1,0,9,100]
排序后,数组变为 [0,1,9,16,100]
示例 2:
输入:nums = [-7,-3,2,3,11]
输出:[4,9,9,49,121]
提示:
- 1 <= nums.length <= 104
- -104 <= nums[i] <= 104
- nums 已按 非递减顺序 排序
进阶:
请你设计时间复杂度为 O(n) 的算法解决本问题
1.思路分析
有序数组,先试试双指针能不能搞,这题目关键在于有了负数的存在,本来最小的数字在平方后可能变成最大的数;所以不断比较数组的两个端点,再把较大的数字倒着插到结果数组即可。
2.代码
时间复杂度:O(n)
空间复杂度:O(n)
class Solution {
public int[] sortedSquares(int[] nums) {
// 创建结果数组
int[] resultArr = new int[nums.length];
// 创建结果数组下标
int k = resultArr.length - 1;
// 遍历,i=0, j = -1, i < =j;
for (int i = 0, j = nums.length - 1; i <= j; ) {
// 判断两头谁大
if (nums[i] * nums [i] < nums[j] * nums[j]) {
// 大的给到结果数组的k下标
resultArr[k--] = nums[j] * nums[j];
// 循环变量 k,指针
j--;
} else {
resultArr[k--] = nums[i] * nums[i];
i++;
}
}
// 返回结果数组
return resultArr;
}
}
209.长度最小的子数组
给定一个含有 n 个正整数的数组和一个正整数 target 。
找出该数组中满足其和 ≥ target 的长度最小的 连续子数组 [numsl, numsl+1, …, numsr-1, numsr] ,并返回其长度。如果不存在符合条件的子数组,返回 0 。
示例 1:
输入:target = 7, nums = [2,3,1,2,4,3]
输出:2
解释:子数组 [4,3] 是该条件下的长度最小的子数组。
示例 2:
输入:target = 4, nums = [1,4,4]
输出:1
示例 3:
输入:target = 11, nums = [1,1,1,1,1,1,1,1]
输出:0
提示:
- 1 <= target <= 109
- 1 <= nums.length <= 105
- 1 <= nums[i] <= 105
进阶:
如果你已经实现 O(n) 时间复杂度的解法, 请尝试设计一个 O(n log(n)) 时间复杂度的解法。
1. 思路分析
有序数组,还是想到双指针(滑动窗口),慢指针当窗口爆掉的时候右移,详细点来说就是定义快慢指针,起点都从0开始,主要遍历移动fast。每移动一次fast,都看看滑动窗口内(从slow -> fast这之间的元素称为滑动窗口)的元素和是不是已经大于target,如果大于target就不断移动slow指向的元素,直到窗口缩短到小于target,就再继续移动fast。
2.代码
时间复杂度:O(n)
空间复杂度:O(1)
class Solution {
public int minSubArrayLen(int target, int[] nums) {
// 定义最小子数组的长度
int minSubarrLen = Integer.MAX_VALUE;
// 定义滑动窗口的元素和
int sum = 0;
// 定义滑动窗口中的快慢指针
int slow = 0;
// 遍历移动快指针
for (int fast = 0; fast <= nums.length - 1; fast++){
// 更新滑动窗口和
sum+=nums[fast];
// 满足条件时
while (sum >= target){
// 更新最小子数组的长度
minSubarrLen = Math.min(minSubarrLen, fast-slow + 1);
// 更新滑动窗口的长度并移动慢指针
sum -= nums[slow++];
}
}
return minSubarrLen == Integer.MAX_VALUE ? 0 : minSubarrLen;
}
}
59. 螺旋矩阵 II
给你一个正整数 n ,生成一个包含 1 到 n2 所有元素,且元素按顺时针顺序螺旋排列的 n x n 正方形矩阵 matrix 。

示例 1:
输入:n = 3
输出:[[1,2,3],[8,9,4],[7,6,5]]
示例 2:
输入:n = 1
输出:[[1]]
提示:
- 1 <= n <= 20
1.思路分析
之前写螺旋矩阵时总纠结转到哪停,转到第几圈,直到今儿刷题解砍到了K神答案,直接低维展开了QAQ,完全不用考虑什么奇数偶数,转几圈。
看下方链接吧
K神的答案直接给我送走
再也不用担心转几圈,到底在哪停了,画一行删掉一行简直优雅至极
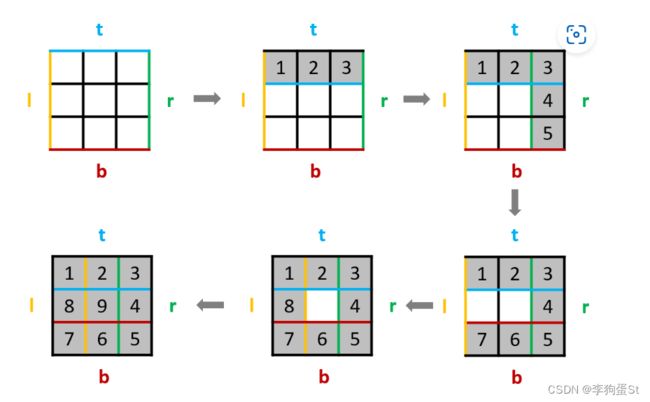
如图,定义了矩阵的4个边界,画完一行就移动一下边界,比我自己纠结着写出来的优雅太多了,看图如果还没理解的话,配上代码也能秒懂了,看图时注意边界彩色线的移动。
2.代码
时间复杂度:O(n^2)
空间复杂度:O(1)
class Solution {
public int[][] generateMatrix(int n) {
// 定义四个边界
int top = 0;
int right = n - 1;
int bottom = n - 1;
int left = 0;
// 定义终点
int target = n * n;
// 定义数字
int num = 1;
// 定义结果数组
int[][] resArr = new int[n][n];
while(num <= target){
// 列动行不动,列从左到右
for (int i = left; i <= right; i++) {
resArr[top][i] = num++;
}
// 第一行写完后上边界该下移了
top++;
// 行动列不动,行从上到下
for (int i = top; i <= bottom; i++){
resArr[i][right] = num++;
}
// 第一列写完后右边界该左移了
right--;
// 列动行不动,列从右到左
for (int i = right; i >= left; i--){
resArr[bottom][i] = num++;
}
// 下边界上移
bottom--;
// 行动列不动,行从下到上
for (int i = bottom; i >= top; i--){
resArr[i][left] = num++;
}
// 左边界右移
left++;
}
return resArr;
}
}
