“哈希表的精髓:深入探索哈希桶数据存储与检索“(附源码+解析)
哈希桶
- 一、哈希桶核心思想
- 二.哈希桶函数接口
-
- Insert函数
- Find函数
- Erase函数
- 复杂度总结
- 三、迭代器
-
- operator++
- 总结
- 四、实现代码+测试代码
-
- HashTable.h
- UnorderedMap.h
- UnorderedSet.h
- Test.cpp
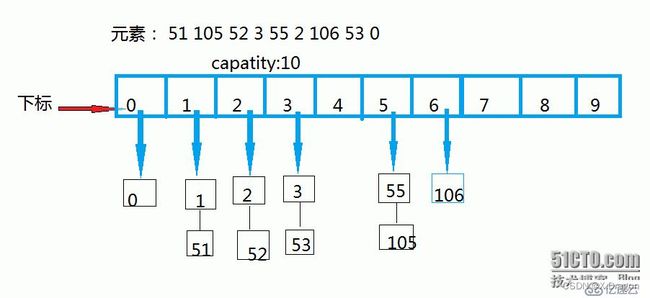
一、哈希桶核心思想
哈希桶(Hash Bucket)是哈希表中解决哈希冲突的一种常用方法,其核心思想是将哈希表的每个槽(slot)扩展为一个桶(bucket),每个桶可以容纳多个元素。
- 核心思想可以总结为以下几点:
-
哈希函数映射:哈希桶利用哈希函数将关键字映射到哈希表的槽(slot)上。哈希函数将关键字转换为一个索引,该索引对应哈希表的槽。
-
桶的存储结构:每个槽被扩展为一个桶,桶是一个链表或其他数据结构,用于存储哈希冲突的元素。当多个关键字映射到同一个槽时,它们将被依次插入到对应槽上的桶中。
-
冲突解决:当发生哈希冲突时,即多个关键字映射到同一个槽上,使用桶来解决冲突。通过在桶中顺序查找或使用其他方法,可以在桶中快速找到目标元素。
-
动态扩容:为了保持哈希表的性能,在哈希桶中设置一个负载因子(load factor)阈值。当哈希表的元素数量接近或超过负载因子阈值时,可以进行动态扩容,即增加哈希表的槽数量,以减少冲突并保持较低的查找时间。
- 哈希桶的核心思想在解决哈希冲突时提供了一种灵活而高效的方法。它允许多个元素共享同一个槽,并通过桶的链式结构实现快速查找和插入。通过合理选择哈希函数和调整负载因子阈值,可以平衡哈希表的性能和空间利用率。哈希桶是实现开散列(Open Addressing)哈希表的重要组成部分,被广泛应用于各种数据结构和算法中。
二.哈希桶函数接口
Insert函数
- 插入函数实现步骤:
-
哈希函数和键提取器:使用哈希函数 hf 和键提取器 kot 对插入的数据进行处理。
-
查找是否存在相同值:通过调用 Find 函数查找是否已存在相同值的元素,如果存在,则返回 false 表示插入失败。
-
动态扩容:检查当前哈希表的大小 _tables.size() 是否达到负载因子 _n,如果是,则进行动态扩容。计算新表的大小 newSize,创建一个新的哈希表 newTable,并将旧表中的数据复制到新表中。
-
插入新元素:计算待插入元素的哈希值 hashi,取模 _tables.size() 获取对应的槽索引。使用头插法,在对应槽的链表中插入新节点 newnode,并更新链表的头指针 _tables[hashi]。
-
更新元素计数:增加哈希表中元素的计数 _n。
-
返回插入结果:返回 true 表示插入成功
- 代码
bool Insert(const T& data)//拉链法/哈希桶
{
HashFunc hf;
KeyofT kot;
if (Find(kot(data))) //不允许值重复
{
return false;
}
//哈希桶一般把负载因子控制为1
if (_tables.size() == _n)
{
size_t newSize = _tables.size() == 0 ? 10 : _tables.size() * 2;
vector<Node*> newTable;
newTable.resize(newSize, nullptr);
for (size_t i = 0; i < _tables.size(); ++i) //把旧表的数据复制到新表
{
Node* cur = _tables[i];
while (cur)
{
Node* next = cur->_next;
size_t hashi = hf(kot(cur->_data)) % newSize;//得到新表的 hashi
cur->_next = newTable[hashi];
newTable[hashi] = cur;
cur = next;
}
_tables[i] = nullptr;
}
newTable.swap(_tables);
}
size_t hashi = hf(kot(data));
hashi %= _tables.size();
//头插法插入新表
Node* newnode = new Node(data);
newnode->_next = _tables[hashi];
_tables[hashi] = newnode;
++_n;
return true;
}
Find函数
- 实现步骤
-
哈希函数和键提取器:使用哈希函数 hf 和键提取器 kot 对待查找的键进行处理。
-
空表检查:如果哈希表 _tables 的大小为 0,表示哈希表为空,直接返回 nullptr。
-
计算哈希值和槽索引:通过哈希函数 hf 计算待查找键的哈希值 hashi。取模 _tables.size() 获取对应的槽索引。
-
遍历链表:从槽索引处获取链表的头指针 cur,进入链表遍历。
-
比较键值:使用键提取器 kot 对当前节点的数据进行处理,与待查找的键进行比较。如果相等,则找到了目标节点,返回指向该节点的指针 cur。
-
更新当前节点:如果当前节点不是目标节点,继续遍历下一个节点 cur = cur->_next。
-
查找结束:遍历完链表仍未找到目标节点,则返回 nullptr 表示未找到。
- 代码
//查找
Node* Find(const K& key)
{
if (_tables.size() == 0)
{
return nullptr;
}
KeyofT kot;
HashFunc hf;
size_t hashi = hf(key);
//size_t hashi = HashFunc()(key);
hashi %= _tables.size();
Node* cur = _tables[hashi];
while (cur)
{
if (kot(cur->_data) == key)
{
return cur;
}
cur = cur->_next;
}
return nullptr;
}
Erase函数
- 实现步骤
-
空表检查:如果哈希表 _tables 的大小为 0,表示哈希表为空,直接返回 false,表示删除失败。
-
哈希函数和键提取器:使用哈希函数 hf 和键提取器 kot 对待删除的键进行处理。
-
计算哈希值和槽索引:通过哈希函数 hf 计算待删除键的哈希值 hashi。取模 _tables.size() 获取对应的槽索引。
-
初始化指针:初始化两个指针 prev 和 cur,prev 指向当前节点的前一个节点,cur 指向当前节点。
-
遍历链表:从槽索引处获取链表的头指针 cur,进入链表遍历。
-
比较键值:使用键提取器 kot 对当前节点的数据进行处理,与待删除的键进行比较。如果相等,则找到了目标节点,执行删除操作。
-
删除节点:根据目标节点的位置进行删除。如果目标节点是头节点(即 prev == nullptr),则更新槽索引处的头指针 _tables[hashi] 为目标节点的下一个节点。如果目标节点不是头节点,则更新前一个节点的指针 prev->_next 为目标节点的下一个节点。
-
释放内存:删除目标节点后,释放其内存空间。
-
返回删除结果:返回 true 表示删除成功。
-
查找结束:遍历完链表仍未找到目标节点,则返回 false,表示删除失败
- 代码
bool Erase(const K& key)
{
if (_tables.size() == 0)
{
return false;
}
HashFunc hf;
KeyofT kot;
size_t hashi = hf(key);
hashi %= _tables.size();
Node* prev = nullptr;
Node* cur = _tables[hashi];
while (cur)
{
if (kot(cur->_data) == key)
{
if (prev == nullptr)
{
_tables[hashi] = cur->_next;
}
else
{
prev->_next = cur->_next;
}
delete cur;
return true;
}
prev = cur;
cur = cur->_next;
}
return false;
}
复杂度总结
- Insert(const T& data) 函数的复杂度:
平均情况下,插入操作的时间复杂度为 O(1),即常数时间。这是因为哈希桶使用拉链法解决冲突,将数据存储在链表中,插入操作只需在对应的链表头部插入新节点。
最坏情况下,插入操作的时间复杂度为 O(n),其中 n 是哈希桶中元素的个数。当哈希桶的负载因子超过阈值,需要进行扩容,将所有元素重新哈希到新的表中。
- Find(const K& key) 函数的复杂度:
平均情况下,查找操作的时间复杂度为 O(1),即常数时间。哈希桶通过哈希函数和槽索引定位到对应的链表,然后在链表中进行查找。
最坏情况下,查找操作的时间复杂度为 O(n),其中 n 是哈希桶中元素的个数。当哈希桶中的所有元素都散列到同一个槽位上,形成一个很长的链表,查找需要遍历整个链表。
- Erase(const K& key) 函数的复杂度:
平均情况下,删除操作的时间复杂度为 O(1),即常数时间。哈希桶通过哈希函数和槽索引定位到对应的链表,然后在链表中进行删除。
最坏情况下,删除操作的时间复杂度为 O(n),其中 n 是哈希桶中元素的个数。当哈希桶中的所有元素都散列到同一个槽位上,形成一个很长的链表,删除需要遍历整个链表。
- 注意
需要注意的是,以上的复杂度分析是基于哈希函数的均匀性和哈希桶的负载因子适中的情况下。当哈希函数的输出不均匀或者负载因子过高时,可能会导致冲突增多、链表变长,进而影响插入、查找和删除的性能。
三、迭代器
operator++
- 实现步骤
- 首先检查当前节点的下一个节点是否存在,如果存在,则迭代器指向下一个节点。
- 如果不存在,则从当前节点所属的桶的哈希值开始,逐个搜索非空桶。
- 如果找到非空桶,则将迭代器指向该桶的第一个节点。
- 如果遍历完所有桶仍未找到非空桶,则将迭代器设置为 nullptr,表示已经到达末尾。
- 迭代器的 operator++() 操作具有常数时间复杂度 O(1),适用于哈希桶的遍历操作。
- 代码
_HTIterator(Node* node, HashTable<K, T, KeyofT, HashFunc>* pht)
{
_node = node;
_pht = pht;
}
Self operator++()
{
if (_node->_next)//桶内++
{
_node = _node->_next;
}
else //桶和桶之间++
{
KeyofT kot;
HashFunc hf;
size_t hashi = hf(kot(_node->_data));//把data用配套仿函数套起来 map就用map set就用set
++hashi;
//找下一个不为空的桶
for (; hashi < _pht->_tables.size(); ++hashi)
{
if (_pht->_tables[hashi])
{
_node = _pht->_tables[hashi];
break;
}
}
//没有找到不为空的桶 用nulllptr去作为end的标识
if (hashi == _pht->_tables.size())
{
_node = nullptr;
}
}
return *this;
}
T& operator*()
{
return _node->_data;
}
T* operator->()
{
return _node->_data;
}
bool operator!=(const Self& s)const
{
return _node != s._node;
}
bool operator==(const Self& s)const
{
return _node == s._node;
}
};
总结
-
Self operator++():自增运算符重载,用于迭代器的前置自增。根据当前迭代器的位置,如果在当前桶内还有下一个节点,则将迭代器指向下一个节点;否则,在桶与桶之间寻找下一个非空桶,并将迭代器指向该桶的第一个节点。函数的时间复杂度为 O(1)。
-
T& operator*():解引用运算符重载,返回当前迭代器所指向节点的数据引用。函数的时间复杂度为 O(1)。
-
T* operator->():箭头运算符重载,返回指向当前迭代器所指向节点的数据指针。函数的时间复杂度为 O(1)。
-
bool operator!=(const Self& s) const:不等运算符重载,判断两个迭代器是否不相等。比较两个迭代器所指向的节点是否相同。函数的时间复杂度为 O(1)。
-
bool operator==(const Self& s) const:等于运算符重载,判断两个迭代器是否相等。比较两个迭代器所指向的节点是否相同。函数的时间复杂度为 O(1)。
-
这些操作使得该迭代器可以用于遍历哈希桶中的元素,通过不断使用自增运算符++来访问下一个节点。解引用运算符*和箭头运算符->用于访问当前节点的数据。等于运算符==和不等运算符!=用于比较两个迭代器是否相等。
-
总体而言,这些迭代器操作的时间复杂度都是 O(1),即常数时间,因为它们只涉及对迭代器的指针操作,不随哈希桶中元素个数的增加而增加。
四、实现代码+测试代码
说明:底层的HashTable通过提高仿函数来设计实现不同的接口,map实现map的仿函数后给定相关的参数然后调用HashTable,set也一样,通过这种方式实现了map和set不同容器调用HashTable,减少了代码的复用,是一种更高维度的泛型编程思维。
HashTable.h
#pragma once
#includeUnorderedMap.h
#pragma once
#include"HashTable.h"
#includeUnorderedSet.h
#pragma once
#include s;
s.insert(2);
s.insert(3);
s.insert(1);
s.insert(2);
s.insert(5);
s.insert(12);
unordered_set<int>::iterator it = s.begin();
//auto it = s.begin();
while (it != s.end())
{
std::cout << *it << " ";
++it;
}
std::cout << std::endl;
for (auto e : s)
{
std::cout << e << " ";
}
std::cout << std::endl;
unordered_set<Date, DateHash> sd;
sd.insert(Date(2022, 3, 4));
sd.insert(Date(2022, 4, 3));
}
}
Test.cpp
#define _CRT_SECURE_NO_WARNINGS
using namespace std;
#include"UnorderedMap.h"
#include"UnorderedSet.h"
int main()
{
GXPYY::test_set();
GXPYY::test_map();
return 0;
}