模糊自适应整定PID控制详解
模糊自适应整定PID控制
-
- 题目
- 流程图
- 代码
- 代码详解
- 运行结果
题目
设被控对象为
G_p (s)=133/(s^2+25s)
采样时间为1ms,采用z变换进行离散化,离散化后的被控对象为
y(k)=-den(2)y(k-1)-den(3)y(k-2)+num(2)u(k-1)+num(3)u(k-2)
位置命令为幅值为1.0的方波信号,r(k) = 1.0。仿真时,先运行模糊推理系统设计程序,实现模糊推理系统d=fuzzpid.fis,并将此模糊推理系统调入内存中,然后运行模糊控制程序。
流程图
代码
模糊控制系统。
clear all;
close all;
a = newfis('fuzzpid');
a = addvar(a,'input','e',[-1,1]);
a = addmf(a,'input',1,'N','zmf',[-1,-1/3]);
a = addmf(a,'input',1,'Z','trimf',[-2/3,0,2/3]);
a = addmf(a,'input',1,'P','smf',[1/3,1]);
a = addvar(a,'input','ec',[-1,1]);
a = addmf(a,'input',2,'N','zmf',[-1,-1/3]);
a = addmf(a,'input',2,'Z','trimf',[-2/3,0,2/3]);
a = addmf(a,'input',2,'P','smf',[1/3,1]);
a = addvar(a,'output','kp',[-10/3,10/3]);
a = addmf(a,'output',1,'N','zmf',[-10/3,-1]);
a = addmf(a,'output',1,'Z','trimf',[-5/3,0,5/3]);
a = addmf(a,'output',1,'P','smf',[1,10/3]);
a = addvar(a,'output','ki',[-1/10,1/10]);
a = addmf(a,'output',2,'N','zmf',[-1/10,-1/30]);
a = addmf(a,'output',2,'Z','trimf',[-2/30,0,2/30]);
a = addmf(a,'output',2,'P','smf',[1/30,1/10]);
rulelist= [1 1 1 2 1 1;
1 2 1 2 1 1;
1 3 1 2 1 1;
2 1 1 3 1 1;
2 2 3 3 1 1;
2 3 3 3 1 1;
3 1 3 2 1 1;
3 2 3 2 1 1;
3 3 3 2 1 1];
a = addrule(a,rulelist);
a1=setfis(a,'DefuzzMethod','centroid');
writefis(a1,'fuzzpid');
a2=readfis('fuzzpid');
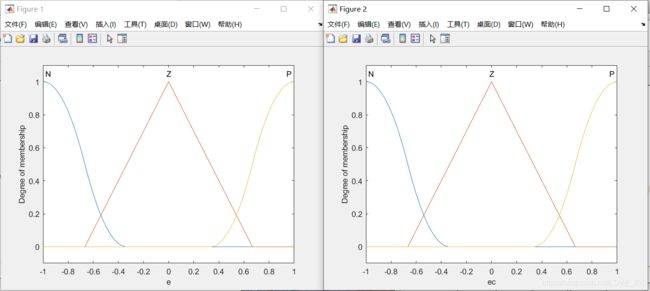
figure(1);
plotmf(a,'input',1);
figure(2);
plotmf(a,'input',2);
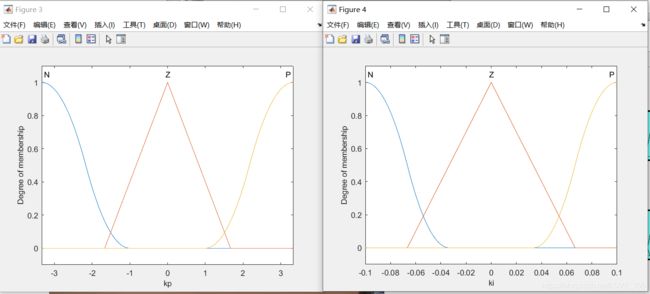
figure(3);
plotmf(a,'output',1);
figure(4);
plotmf(a,'output',2);
figure(5);
plotfis(a);
fuzzy fuzzpid;%定义该模糊系统的名称。
ruleview fuzzpid;
模糊自适应调整。
clear all;
close all;
warning off;
a = readfis('fuzzpid');
ts = 0.001;
sys = tf(133,[1,25,0]);
dsys = c2d(sys,ts,'z');%z变换进行离散化
[num,den] = tfdata(dsys,'v');
u_1 = 0;
u_2 = 0;
y_1 = 0;
y_2 = 0;
e_1 = 0;
ec_1 = 0;
ei = 0;
kp0 = 0;
ki0 = 0;
for k = 1:1:1000
time(k) = k *ts;
r(k) = 1;
k_pid = evalfis([e_1,ec_1],a);%模糊化e_1,ec_1得到∆kp,∆ki
kp(k) = kp0 + k_pid(1);%修正kp,计算kp
ki(k) = ki0 + k_pid(2);%修正ki,计算ki
u(k) = kp(k)*e_1 + ki(k)*ei;
y(k) = -den(2)*y_1-den(3)*y_2+ num(2)*u_1 + num(3)* u_2;
e(k) = r(k) - y(k);
u_2 = u_1;
u_1 = u(k);
y_2 = y_1;
y_1 = y(k);
ei = ei + e(k) *ts;
ec(k) = e(k) - e_1;
e_1 = e(k);
ec_1 = ec(k);
end
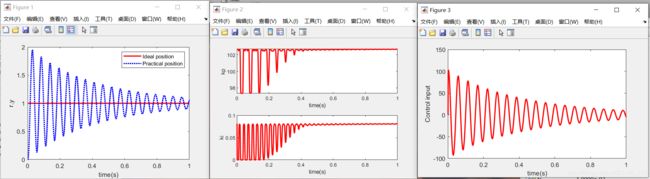
figure(1);
plot(time,r,'r',time,y,'b:','linewidth',2);
xlabel('time(s)');
ylabel('r,y');
legend('Ideal position','Practical position');
figure(2);
subplot(211);
plot(time,kp,'r','linewidth',2);
xlabel('time(s)');
ylabel('kp');
subplot(212);
plot(time,ki,'r','linewidth',2);
xlabel('time(s)');
ylabel('ki');
figure(3);
plot(time,u,'r','linewidth',2);
xlabel('time(s)');
ylabel('Control input');
代码详解
模糊控制系统
由题意得我们需要建立如下图所示的模糊控制系统

模糊控制系统的详解可以参考链接: https://blog.csdn.net/LOVE_105/article/details/112135599.
模糊控制系统流程
1)确定模糊控制器的结构
控制器的输入为e(误差),ec(误差变化率)
控制器的输出为kp,ki
(2)定义输入、输出的模糊集
ec定义为3个模糊集:N、Z、P
e定义为3个模糊集:N、Z、P
kp定义为3个模糊集:N、Z、P
ki定义为3个模糊集:N、Z、P
(3)定义隶属函数
e和ec模糊集相同,采用相同的隶属函数。
(4)建立模糊控制规则
建立如图所示的模糊控制规则

rulelist= [1 1 1 2 1 1;
1 2 1 2 1 1;
1 3 1 2 1 1;
2 1 1 3 1 1;
2 2 3 3 1 1;
2 3 3 3 1 1;
3 1 3 2 1 1;
3 2 3 2 1 1;
3 3 3 2 1 1];
(5)建立模糊控制集
(6)模糊推理
(7)仿真实例
模糊自适应调整
利用模糊PID控制器结构图进行仿真模拟
运行结果
 模糊自适应调整
模糊自适应调整
取kp0 = 0;ki0 = 0;
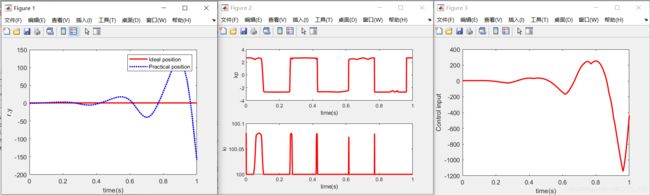
 取kp0 = 100;ki0 = 0;
取kp0 = 100;ki0 = 0;
 振荡次数增多,系统变得不稳定。
振荡次数增多,系统变得不稳定。
取kp0 = -1;ki0 = 0;

系统的响应速度缓慢
取kp0 = 0;ki0 =100;
 引起响应过程的较大超调
引起响应过程的较大超调
取kp0 = 0;ki0 =-1; 有一定的系统稳态误差,影响系统的调节精度。
有一定的系统稳态误差,影响系统的调节精度。
比例系数 Kp的作用是加快系统的响应速度,提高系统的调节精度,Kp加大,将使系统响应速度加快,Kp偏大时,系统振荡次数增多,调节时间加长;Kp太小又会使系统的响应速度缓慢。
积分系数 Ti的作用是消除系统的稳态误差,Ti越大,系统的稳态误差消除越快,但是当Ti 过大时,会引起响应过程的较大超调;若 Ti过小, 将使系统稳态误差难以消除,影响系统的调节精度。