python 基础知识点(蓝桥杯python科目个人复习计划23)
今日复习内容:基础算法中的枚举
一.枚举
1.定义
枚举是通过逐个尝试所有可能的值或组合来解决问题的方法。
也就是将问题空间划分为一系列离散的状态,并通过遍历这些离散的状态来寻找解决问题的方法。
例如,有一个方程X*X + Y*Y = 100,求满足方程的整数解。
用枚举的方法,就是遍历[-10,10]上的x值和y值,找出满足条件的解。
2.流程
用上面那个例子
(1)确定解空间(一维还是二维等);
(2)确定空间边界(每个变量最小值,最大值,步长) ;
(3)估算时间复杂度;
(4)如果步骤三无法通过,通过减少枚举空间,变换枚举顺序等策略,重新从第一个步骤开始迭代。
3.思路介绍
也是用一个题
题目:公鸡五文钱一只,母鸡三文钱一只,小鸡三只一文钱。现在有100文,想买100只鸡,求方案。
思路:假设公鸡x只,母鸡y只,小鸡z只,则有以下关系式:
x + y + z = 100
5x + 3y + 1/3z = 100
三个方法:
(1)枚举x,枚举y,枚举z;
(2)枚举x,枚举y;
(3)枚举z。
OK,这些是开胃的,温馨提示,接下来的题有点多。
4.例题讲解
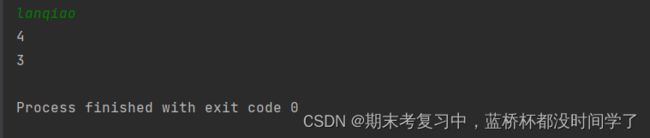
举例1:字符计数
题目描述:
给定一个单词,请计算这个单词中有多少个元音字母和多少个辅音字母。
元音字母是a,e,i,o,u,共5个,其余均为辅音。
输入描述:
输入格式:输入一个单词,单词中仅包含大写字母和小写字母,单词中的字母个数不能超过100个。
输出描述:
输出两行,第一行包括一个整数,表示元音字母的数量;第二行包括一个整数,表示辅音字母的数量。
参考答案:
s = input()
sum1,sum2 = 0,0
for c in s:
if c in 'aeiou':
sum1 += 1
else:
sum2 += 1
print(sum1)
print(sum2)运行结果:
这个题比较浅显易懂,我就不写思路解析和代码解释了。
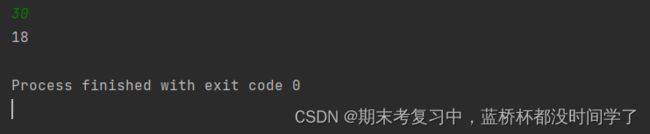
举例2:反倍数
题目描述:
给定三个整数a,b,c,如果一个整数既不是a的倍数,也不是b的倍数,还不是c的倍数,则称这个数为反倍数。
请问1至n中共有多少个反倍数?
输入描述:
输入的第一行包括一个整数n;
第二行包括三个整数a,b,c,相邻两个数之间用一个空格隔开;
其中,1 <= n <= 10^6 , 1 <= a <= n , 1 <= b <= n , 1 <= c <= n.
输出描述:
输出一行包括一个整数,表示答案。
参考答案:
n = int(input())
ans = 0
a,b,c = map(int,input().split())
for i in range(1,n+1):
if i % a != 0 and i % b != 0 and i % c != 0:
ans += 1
print(ans)运行结果:
这个题也很好理解,不做过多解释。
搞个拓展:
容斥定理:
1到n中a的倍数有 n // a 个,1到n中b的倍数有 n // b 个,1到n中ab的倍数有 n // ab 个,1到n中既是a的倍数又是b的倍数的有 n // a + n // b - n // ab 个。
举例3:洁净数
题目描述:
小明非常不喜欢数字2,包括那些数位上包含数字2的数,如果一个数的数位上均不含有数字2,小明称它为洁净数。
请问在整数1到n中,有多少个洁净数?
输入描述:
输入的第一行包括一个整数n(1 <= n <= 10^6)。
输出描述:
输出一行包括一个整数,表示答案。
参考答案:
n = int(input())
ans = 0
for i in range(1,n+1):
if '2' not in str(i):
ans += 1
print(ans)运行结果:
这个题也还行,不做过多解释。
举例4:扫雷
题目描述:
在一个m行n列的方格图上有一些位置有地雷,另外一些位置为空,请为每一个空位置标一个整数,表示周围8个相邻的方格中有多少个地雷。
输入描述:
输入的第一行包括两个整数n和m
第二行到第n+1行每行包括m个整数,相邻整数之间用一个空格包括。如果对应的整数为0,表示这一格没有地雷,如果对应的整数为1,表示这一格有地雷。
其中,1 <= n,m <= 100。
输出描述:
输出n行,每行m个整数,相邻整数之间用空格分开
对于没有地雷的方格,输出这格周围的地雷数量,对于有地雷的方格,输出9。
参考答案:
def input_list():
return list(map(int,input().split()))
n,m = input_list()
a = []
for i in range(n):
a.append(input_list())
b = [[0] * m for i in range(n)]
dir = [(1,0),(0,1),(-1,0),(0,-1),(-1,-1),(-1,1),(1,-1),(1,1)]
# 枚举第i行,枚举第j列
for i in range(n):
for j in range(m):
if a[i][j] == 1:
b[i][j] = 9
else:
b[i][j] == 0
for k in range(8):
x,y = i + dir[k][0],j + dir[k][1]
if 0 <= x < n and 0 <= y < m:
b[i][j] += a[x][y]
print(b[i][j],end = ' ')
print()OK,这个题有难度,我来解释一下。
(1)[[0] * m for i in range(n)]:这个表示创建一个n行m列的矩阵;
(2)取定一个方格,它周围有8个值(正上,正下,正左,正右,左上,左下,右上,右下);
这样说没意思,我来写出来。
#取定一个点(x,y)
(x - 1,y - 1),(x - 1,y + 0),(x - 1,y + 1)
(x + 0,y - 1),(x + 0,y + 0),(x + 0,y + 1)
(x + 1,y - 1),(x + 1,y + 0),(x + 1,y + 1)这个东西看不懂的话,欢迎来问我,只要有时间,我一定回。
(3)
dir = [(1,0),(0,1),(-1,0),(0,-1),(-1,-1),(-1,1),(1,-1),(1,1)]
我举个例子;中间值取(x + 0,y + 0),左边是(x + 0,y - 1),右边是(x + 0,y + 1),上面是(x - 1,y + 0),则dir存储的是(x - 1)-(x - 0) = -1,(x - 0)-(x + 1) = -1,(y - 1)-(y - 0) = -1,即它旁边8个方位的差值,就是x,y后面的数字,并用坐标形式表示。
(4)
if a[i][j] == 1:
b[i][j] = 9
else:
b[i][j] == 0
这个地方是按照题目给的要求写的,有地雷(这部分代码的第一行)则对应位置是9,否则就是0;
for k in range(8): # x,y = i + dir[k][0],j + dir[k][1] # if 0 <= x < n and 0 <= y < m: # b[i][j] += a[x][y]
这部分是说,那个位置没有地雷就计算旁边的地雷数,8个方位,所有括号里面是8,这部分代码的第二行是指从当前位置移向第k个位置。最后两行是判断所到位置是否在规定范围内,并统计。
OK,今天写到这里,如果有不懂的可以问我,我都会回的。好了,明天继续!