机器学习周记（第十八周：GAN.pt3）2023.11.20~2023.11.26
目录
摘要
ABSTRACT
1 文献阅读
2 生成结果多样性判别（Diversity）
3 生成结果多样性判别（Frechet Inception Distance (FID)）
4 条件对抗生成网络（Conditional GAN，CGAN）
5 无监督条件对抗生成网络（Unsupervised Conditional Generation）
6 相关代码
摘要
本周继续了GAN相关内容的学习，明白了即使GAN能按照需求正常生成图片，仍然存在生成图像多样性不足的问题，比如生成的人像都是一种肤色，这是GAN创造力不足的体现。想要客观地评判GAN生成结果是否多样化，可以使用Diversity和FID两种方法判别。除此以外还学习了Conditional GAN（CGAN），在有标注样本的情况下让GAN根据我们输入的条件生成图像，以及进一步学习了Unsupervised Conditional Generation，在没有标注样本的情况下让GAN根据我们输入的条件生成图像。
本周阅读了一篇基于改进果蝇算法的LSTM水质时间序列预测的论文，该文章主要用到了STL分解时间序列，再将分解的时间序列输入LSTM中进行预测，最后拟合所有的预测结果得到最终的预测结果，以及使用基于高斯函数设计动态改变搜索半径的果蝇算法来更新LSTM的超参数。
ABSTRACT
This week, We continued our study of GAN-related content and gained an understanding that even when GANs can generate images according to specified requirements, there remains an issue of insufficient diversity in the generated images. For instance, all generated portraits might share a common skin tone, reflecting a lack of creativity in GANs. To objectively assess the diversity of GAN-generated results, two methods, Diversity and FID, can be employed for discrimination. Additionally, We explored Conditional GANs (CGANs), which enable GANs to generate images based on specified conditions when labeled samples are available. Furthermore, We delved into Unsupervised Conditional Generation, allowing GANs to generate images based on provided conditions in the absence of labeled samples.
This week, We also read a paper on LSTM-based water quality time series prediction using an improved FOA algorithm. The article primarily utilized STL decomposition of time series, inputting the decomposed time series into LSTM for prediction, and finally fitting all prediction results to obtain the ultimate prediction result. The paper also incorporated the FOA algorithm that dynamically adjusts the search radius based on Gaussian functions to update the hyperparameters of LSTM.
1 文献阅读
论文标题：基于改进果蝇算法的LSTM在水质预测中的应用
论文摘要：水质环境的实时变化和内部耦合导致难以实现水质高效准确的预测。为挖掘水质时间序列中的更多信息，同时提高预测模型的精度，提出一种溶解氧（Dissolved Oxygen，DO）组合预测模型。首先将水质数据去耦合，进行时间序列分解，然后将分解后趋势分量、周期分量和余项分量输入到长短时神经网络模型(LSTM)中进行预测，再针对LSTM网络初始化参数对预测性能的影响提出基于高斯函数的果蝇算法进行优化，最后将各分量的预测值重构为溶解氧浓度的预测值。以海河某3个河流断面的水质数据进行仿真检验，结果表明混合模型对3个站点溶解氧浓度预测效果好，误差小，泛化性强。
论文模型：为分析数据内部耦合特性，论文将基于局部加权回归散点平滑法的周期性和趋势性分解(Seasonal and Trend decomposition using Loess, STL)方法用于水质预测中，将水质数据时间序列分为三部分：趋势序列、周期序列和余项序列；同时针对网络易收敛于局部最优的缺点，本文通过高斯函数设计动态改变搜索半径改进果蝇算法，从而快速优化网络参数，分别建立周期、趋势和余项预测模型；最后将3个预测结果进行拟合，组合模型预测结果好。
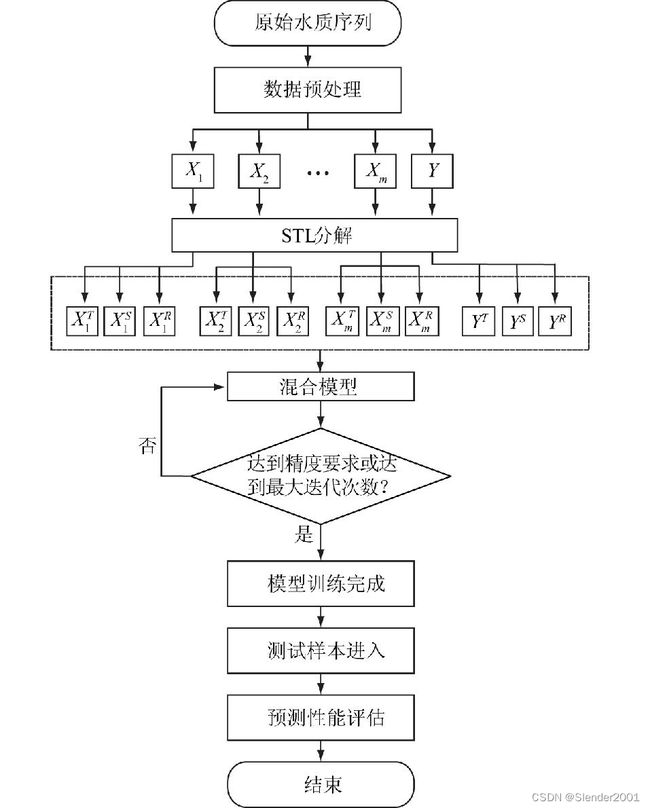GNFOA-STL-LSTM混合模型结构示意图
（1）首先将原始水质序列进行预处理，增补缺失值和去除异常值后，得到一个9维的数组：
,
,
,
,
,
,
,
,
。其中为DO浓度，
为其他8种水质。
（2）充分考虑数据的时序特性，减少同一指标内部趋势分量、周期分量和余项分量之间的相互耦合，降低预测误差，通过STL将水质数据进行分解重组，得到3个不同特性的9维的数组。
![T=\left [ X_{1}^{T},X_{2}^{T},X_{3}^{T},X_{4}^{T},X_{5}^{T}X_{6}^{T},X_{7}^{T},X_{8}^{T},Y^{T} \right ],](http://img.e-com-net.com/image/info8/aaa89ec18f634268aa267d6b07ccc0e4.png){kind=small}
![S=\left [ X_{1}^{S},X_{2}^{S},X_{3}^{S},X_{4}^{S},X_{5}^{S}X_{6}^{S},X_{7}^{S},X_{8}^{S},Y^{S} \right ],](http://img.e-com-net.com/image/info8/15eaf42145064149bc521df1e910c58b.png){kind=small}
![R=\left [ X_{1}^{R},X_{2}^{R},X_{3}^{R},X_{4}^{R},X_{5}^{R}X_{6}^{R},X_{7}^{R},X_{8}^{R},Y^{R} \right ],](http://img.e-com-net.com/image/info8/be762360d1c54c628ff84fd228853530.png){kind=small}
（3）为充分提取输入特征的特征相关性和时序相关性，通过3个独立LSTM模型分别对3个序列进行训练，得到3个预测结果
、
、
，进行拟合得到最终的DO浓度预测结果
，
。
水质STL分解重构模型：STL是利用鲁棒性局部加权回归作为平滑方法的时间序列分解方法，时间序列数据被分解为趋势分量
、周期分量
和余项
，即
。
STL分为2个过程，内循环主要负责分解趋势分量和周期分量；外循环主要根据剩余数据为下一轮内循环分配稳健性权重，减少异常值的影响。单一的模型对于时间序列预测存在一定的局限性，同时各个水质指标之间相互耦合、相互影响，水质数据在时间上具有一定周期性，将输入水质序列利用STL进行分解，得到水质数据的周期性、趋势性和余项分量，即
。
加法模型适合于随时间变化趋势较为单调的情况，由于水质序列有较大的波动，故本文选用乘法模型。由于STL仅能处理加法模式的分解，对于乘法分解需要将乘法转换为加法处理完后再逆变回去。本文使用lg函数进行转换，即
。
模型输入为数据中剩余8种元素经STL分解后的数据重构为周期序列、趋势序列和余项序列，时间窗口大小为T，分别输入3个GNFOA-LSTM预测模型。周期序列输入模型进行训练构建S-GNFOA-LSTM，趋势序列输入模型进行训练构建T-GNFOA-LSTM，余项序列输入模型进行训练构建R-GNFOA-LSTM，得到3个模型对DO分解的各分量预测结果
、
和
，由公式
拟合DO浓度最终预测结果
。
基于高斯函数变半径的果蝇改进算法(Gaussian Network-based Fruit Fly Optimization Algorithm，GNFOA)：论文模型需设置的初始化参数包括：LSTM循环次数L、窗口长度m与神经元个数r，记LSTM(L,m,r)为训练后的模型，由于不同的超参数对模型的预测精度有较大影响，为使模型效果达到最优，本文采用改进的果蝇算法进行参数搜索。借鉴了粒子群算法的思想，典型果蝇优化算法(Fruit Fly Optimization Algorithm, FOA)可应用于求解全局最优解。典型FOA算法中，果蝇个体按照固定半径R进行搜索，R的大小与优化精度有直接性的关系。本文提出了改进FOA算法，该算法中搜索半径R满足
。
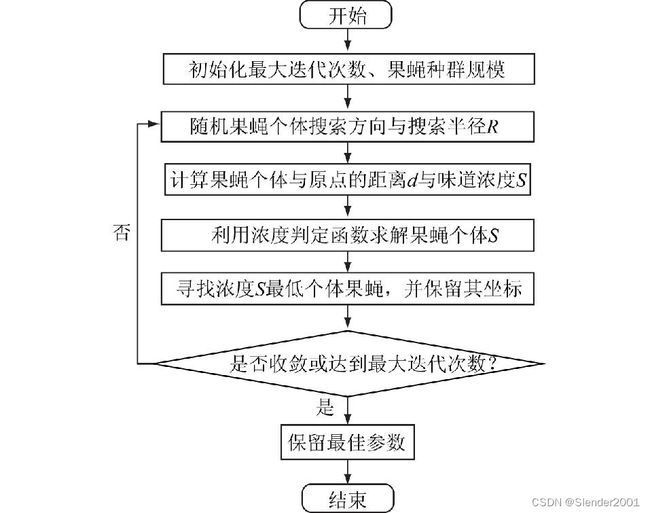改进果蝇算法的模型优化过程
具体步骤如下：
步骤1：将模型参数的组合(L,m,r)设置为GNFOA的三维搜索空间，各超参数的取值范围不超过上下限。取果蝇数量为M,将其随机分布于参数的三维空间。
步骤2：赋予果蝇个体利用嗅觉搜寻食物的随机距离与方向，果蝇搜索半径为R并按照公式进行递减。
步骤3：设第i只果蝇与原点的欧式距离为
。味道浓度
为欧式距离的倒数。
步骤4：通过浓度判定函数
求解果蝇个体的味道浓度。
步骤5：通过将浓度判定值代入浓度判定函数中求出果蝇个体的味道浓度，并找出该果蝇群体味道浓度为最大值的果蝇，保留其坐标，其余果蝇在该坐标周围继续搜索。
步骤6：重复步骤2至步骤5，若当前味道浓度优于前一迭代味道浓度，则执行步骤5，直到达到迭代次数最大为止。最后保留最佳参数模型，即最优预测模型。
实验结果：
2 生成结果多样性判别（Diversity）
要解决判断GAN的生成结果是否出现Diversity不足的问题，可以把一组generated data输入CNN Classifier，然后把得到的各分类概率分布取平均作为结果。如果这个平均概率分布中，各类别的分布比较平均，那就说明generated data有足够的Diversity。
这产生了一个新的问题，为什么Quality of Image部分说要概率分布集中在某个类别好，而本部分的Diversity又说要概率分布均匀好，是否互相矛盾呢？看Quality of Image时，Classifier的输入是一张图片。看Diversity时，Classifier的输入是Generater生成的所有图片，对所有的输出取平均来衡量。Inception Score (IS)就是结合了Quality of Image和Diversity。Quality高, Diversity大，对应的IS就大。
对于特定人脸生成的图像，不能用Inception Score，因为都是人脸图片，Classifier都识别为一类，因此Diveristy不高。因此不是所有的GAN都适合使用Diveristy来判断生成结果是否多样。
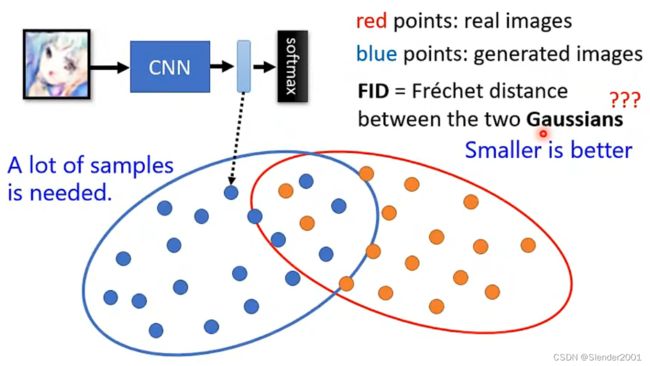
3 生成结果多样性判别（Frechet Inception Distance (FID)）
解决方法不适用Diveristy的方法就是使用Frechet Inception Distance (FID)。如下图所示，分析 CNN的输出，也是Softmax的输入，这部分向量之间是保留有较大差异的。图中红色点是真实的图像，蓝色点表示生成的图像，FID计算的是两个Gaussian Distribution之间的Frechet Distance（假设真实和生成的图像都是Gaussian Distribution），Frechet Distance越小越好。
但是，对于GAN来说，完全依赖这些指标来判断好坏是没有意义的，有时生成图片的Quality和 FID都不错，生成图片的质量也能满足我们的要求，但可能从某种程度上太符合要求了（极端的例子，生成图片和真实图片一模一样），比如下图所示的图片。
可是我们希望机器能生成新的图片，如果和训练图片一模一样，直接到训练图片集采样就好了。应对方法就是计算generated data和real data的相似度，看是不是一样。但这也产生新的问题，机器可能会学到把训练图片左右反转一下，如上图中第三行图片所示，计算相似度是不同，其实还是原图片。所以说，衡量Generative Model的好坏并不是单纯依靠指标就能完成的。
4 条件对抗生成网络（Conditional GAN，CGAN）
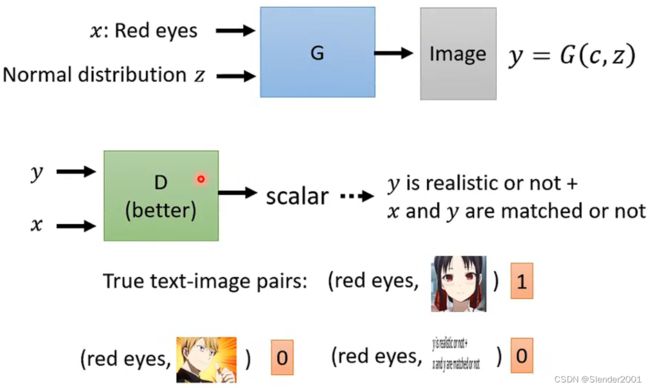
现在，我们学习的GAN能够在随机分布sample的输入下生成我们想要的图片，但这还不够完美，我们还希望GAN还兼顾人类输入的条件来生成结果。一种典型的应用情景就是，GAN能对人类输入的文字描述生成对应的图像（Text-to-image），当然这需要文字对应描述的真实图像进行训练。每一个训练图像都包含很多个文字描述标签，例如“red eye”、“yellow hair”、“black clothes”等，当我们输入文字描述时，GAN通过对应文字描述的图片生成结果。输入的文字描述当然不能直接作为GAN的输入，可以先放进RNN或者Transformer中进行处理，再输入GAN之中。GAN之所以能够根据文字描述输出不同但是符合要求的图片，这取决于每次从分布中sample出来的输入GAN的向量的不同。
因为引入了输入
，所以最初设计的Discriminator不再满足CGAN的要求。之所以这样，是因为之前的Discriminator只识别图像是否是机器生成的，这就会让Generator投机取巧，尽可能的生成更加高清且真实的图片去骗过Discriminator而完全忽略输入的条件。
所以，需要针对CGAN的Discriminator进行调整，将输入条件也作为Discriminator的输入，这样就能兼顾图像真实度和输入条件的符合程度了。但这样的训练方法往往也不够好，还需要在训练资料里参入大量标签与图片不符的数据，并且告诉Discriminator这些数据也要判别为不好的图像。
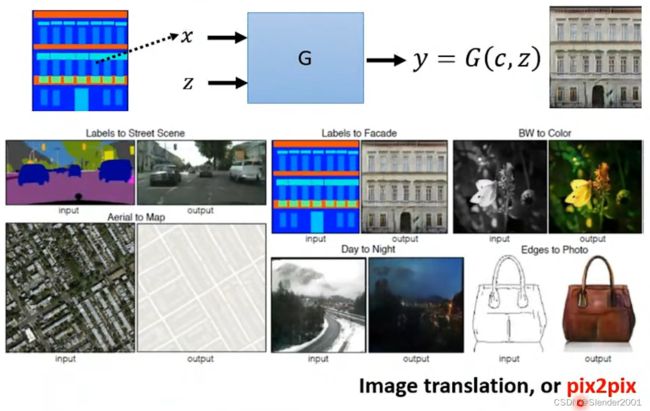
当然CGAN的应用远不止于此，除了Text-to-image外，还可以是pix2pix，让GAN根据图片来生成图片。比如说，输入一个房屋结构草图，输出房屋根据草图建好后的图像；输入一张黑白图像，输出对应的彩色版本；输入一张画，输出这张画对应于现实世界可能的样子。甚至可以是Sound-to-image，根据声音来生成图片。
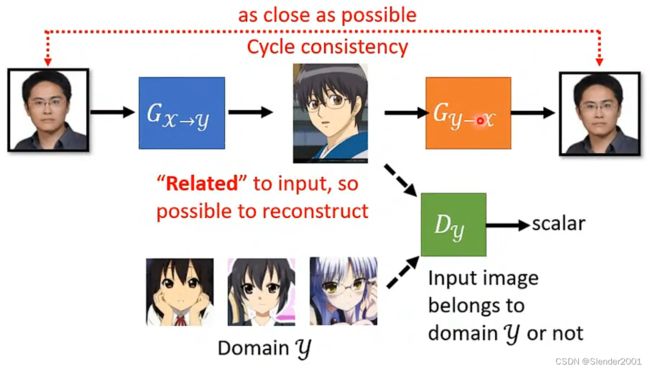
5 无监督条件对抗生成网络（Unsupervised Conditional Generation）
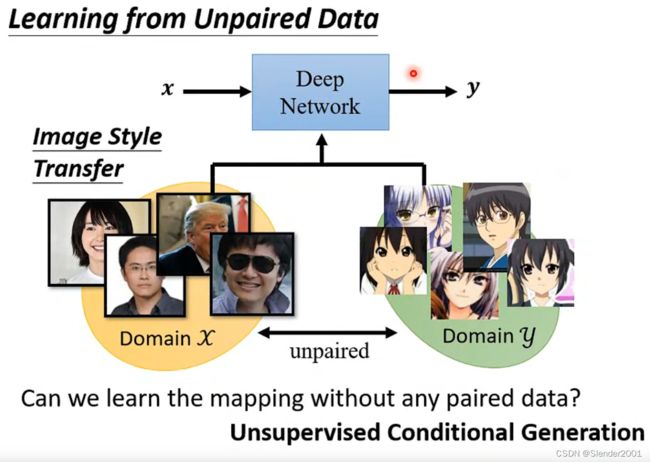
之前学习的GAN都是基于已经标注好的训练资料，如果是无监督情况下GAN要如何生成我们想要的结果呢？用一个现实的例子来说明，输入一张真实的人脸如何将人脸转换成对应的卡通形象，这显然是很难找到训练资料的。
一般GAN的解决方案是输入一张真实人脸分布的图片，输入一张生成的图片，再让这张生成的图片由卡通人脸分布图片训练的鉴别器进行鉴别。虽然确实可以让生成器生成卡通人脸图片，但是生成的结果会完全忽略生成器输入的真实人脸图片，随意地输出卡通图片。
因此，需要Cycle GAN。什么是Cycle GAN？Cycle GAN就是在真实人脸转成卡通人脸之后，再将卡通人脸转回真实人脸，这样循环生成图像的GAN就是Cycle GAN。最终转回的生成真实人脸要和输入真实人脸越接近越好。
6 相关代码
STL分解时间序列数据：
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from statsmodels.tsa.seasonal import STL
# 生成示例时间序列数据
date_rng = pd.date_range(start='2023-01-01', end='2023-03-01', freq='D')
data = np.random.randn(len(date_rng))
ts = pd.Series(data, index=date_rng, name='Variable1')
print(ts)
# 进行STL分解
stl = STL(ts, seasonal=13) # 13表示季节性的周期，可以根据实际情况调整
result = stl.fit()
# 获取分解后的三个部分
trend = result.trend
seasonal = result.seasonal
residual = result.resid
# 可视化分解结果
plt.figure(figsize=(10, 6))
plt.subplot(4, 1, 1)
plt.plot(ts.index, ts.values, label='Original', color='blue')
plt.legend(loc='lower right')
plt.subplot(4, 1, 2)
plt.plot(trend.index, trend, label='Trend', color='orange')
plt.legend(loc='lower right')
plt.subplot(4, 1, 3)
plt.plot(seasonal.index, seasonal, label='Seasonal', color='green')
plt.legend(loc='lower right')
plt.subplot(4, 1, 4)
plt.plot(residual.index, residual, label='Residual', color='red')
plt.legend(loc='lower right')
plt.tight_layout()
plt.show()运行结果：
