详细介绍 Go 中如何实现 bitset

最近尝试在 B 站录些小视频，我的 B 站主页。录视频当是为了彻底搞懂某个知识点的最后一步吧，同时也希望能习得一些额外的能力。在讲 Go 如何实现 bitset 的时候，发现这块内容有点难讲。思考后，我决定通过文字辅以视频的方式说明，于是就写了这篇文章。

相关代码已经放在了 github，地址如下：go-set-example

如果发现有什么不妥的地方，欢迎大佬们指正，感谢。

bitset 结构

之前我已经写过一篇题为 Go 中如何使用 Set 的文章，其中介绍了 bitset 一种最简单的应用场景，状态标志位，顺便还提了下 bitset 的实现思路。

状态标志和一般的集合有什么区别呢？

我的总结是主要一点，那就是状态标志中元素个数通常是固定的。而一般的集合中，元素个数通常是动态变化的。这会导致什么问题？

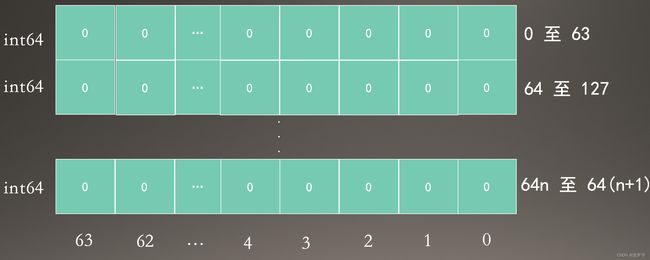
一般，我们使用一个整数就足以表示状态标志中的所有状态，最大的 int64 类型，足足有 64 个二进制位，最多可以包含 64 个元素，完全足够使用。但如果是集合，元素数量和值通常都不固定。

比如一个 bitset 集合最初可能只包含 1、2、4 几个元素，只要一个 int64 就能表示。如下：

但如果再增加了一个元素，比如 64（一个 int64 的表示范围是 0-63），这已经超出了一个 int64 能表示的范围。该怎么办？

一个 int64 无法表示，那就用多个呗。此时的结构如下：

一个 int64 切片正好符合上面的结构。那我们就可以定义一个新的类型 BitSet，如下：

type BitSet struct {
	data []int64
	size int
}

data 成员用于存放集合元素，切片的特点就是能动态扩容。

还有，因为 bitset 中元素个数无法通过 len 函数获取，而具体的方法相对复杂一点，可增加一个 size 字段记录集合元素的个数。然后就可以增加一个 Size 方法。

func (set *BitSet) Size() int {
	return set.size
}

元素位置

定义好了 BitSet 类型，又产生了一个新的问题，如何定位存放元素的位置？在标志位的场景下，元素的值即是位置，所以这个问题不用考虑。但通用的集合不是如此。

先看下 BitSet 的二进制位的分布情况。

类似行列的效果，假设用 index 表示行（索引），pos 表示列（位置）。切片索引从 0 到 n，n 与集合中的最大元素有关。

接下来确定 index 和 pos 的值。其实，之前的文章已经介绍过了。

index 可通过元素值整除字长，即 value / 64，转化为高效的位运算，即 value >> 6。

pos 可以通过元素值取模字长，即 value % 64，转化为高效的位运算，即 value & 0x3f，获取对应位置，然后用 1 << uint(value % 0xf) 即可将位置转化为值。

代码实现

理论再多，都不如 show me your code。开始编写代码吧！

先定义一些常量。

const (
	shift = 6    // 2^n = 64 的 n
	mask  = 0x3f // n=6，即 2^n - 1 = 63，即 0x3f
)

就是前面提到的用于计算 index 和 pos 的两个常量。

提供两个函数，用于方便 index 和 pos 上对应值的计算，代码如下：

func index(n int) int {
	return n >> shift
}

// 相对于标志位使用场景中某个标志的值
func posVal(n int) uint64 {
	return 1 << uint(n&mask)
}

构造函数

提供了一个函数，用于创建初始 BitSet，且支持设置初始的元素。

函数原型如下：

func NewBitSet(ns ...int) *BitSet {
	// ...
}

输出参数 ns 是一个 int 类型的变长参数，用于设置集合中的初始值。

如果输入参数 ns 为空的话，new(BitSet) 返回空集合即可。

if len(ns) == 0 {
	return new(BitSet)
}

如果长度非空，则要计算要开辟的空间，通过计算最大元素的 index 可确定。

// 计算多 bitset 开辟多个空间
max := ns[0]
for _, n := range ns {
	if n > max {
		max = n
	}
}

// 如果 max < 0，直接返回空。
if max < 0 {
	return new(BitSet)
}

// 通过 max >> shift+1 计算最大值 max 所在 index
// 而 index + 1 即为要开辟的空间
s := &BitSet{
	data: make([]int64, index(max)+1),
}

现在，可以向 BitSet 中添加元素了。

for _, n := range ns {
	if n >= 0 {
		// e >> shift 获取索引位置，即行，一般叫 index
		// e&mask 获取所在列，一般叫 pos，F1 0 F2 1
		s.data[n>>shift] |= posVal(n)
		// 增加元素个数
		s.size++
	}
}

// 返回创建的 BitSet
return s

元素已经全部添加完成！

BitSet 的方法

接下来是重点了，为 BitSet 增加一些方法。主要是分成两类，一是常见的增删查等基础方法，二是集合的特有操作，交并差。

基础方法

主要是几个方法，分别是 Add（增加）、Clear（清除） 、Contains（检查）以及返回元素个数。如果要有更好的性能和空间使用率，Add 和 Clear 还有考虑灵活的。

contains

先讲 Contains，即检查是否存在某个元素。

函数定义如下：

func (set *BitSet) Contains(n int) bool {
	...
}

输入参数即是要检查的元素，输出是检查结果。

实现代码如下：

// 获取元素对应的 int64 的位置，如果超出 data 能表示的范围，直接返回。
i := index(n)
if i >= len(set.data) {
	return false
}

return set.data[i]&posVal(n) != 0

核心就是 set.data[i]&posVal(n) != 0 这句代码，通过它判断是否存在指定元素。

clear

再谈 Clear，从集合中清除某个元素，

函数定义如下：

func (set *BitSet) Clear(n int) *BitSet {
	// ...
}

实现代码如下：

// 元素不能小于 0
if n < 0 {
	return set
}

// 计算切片索引位置，如果超出当前索引表示的范围，返回即可。
i := index(n)
if i >= len(set.data) {
	return set
}

// 检查是否存在元素
if d[i]&posVal(n) != 0 {
	set.data[i] &^= posVal(n)
	set.size--
}

通过 &^ 实现指定位清除。同时要记得set.size-- 更新集合中元素的值。

上面的实现中有个瑕疵，就是如果一些为被置零后，可能会出现高位全部为 0，此时应要通过 reslice 收缩 data 空间。

具体怎么操作呢？

通过对 set.data 执行检查，从高位检查首个不为 0 的 uint64，以此为基准进行 reslice。假设，这个方法名为 trim。

实现代码如下：

func (set *Set) trim() {
	d := set.data
	n := len(d) - 1
	for n >= 0 && d[n] == 0 {
		n--
	}
	set.data = d[:n+1]
}

add

接着，再说 Add 方法，向集合中添加某个元素。

函数定义如下：

func (set *BitSet) Add(n int) *BitSet {
	...
}

增加元素的话，先检查下是否有足够空间存放新元素。如果新元素的索引位置不在当前 data 表示的范围，则要进行扩容。

实现如下：

// 检测是否有足够的空间存放新元素
i := index(n)
if i >= len(set.data) {
	// 扩容大小为 i+1
	ndata := make([]uint64, i+1)
	copy(ndata, set.data)
	set.data = ndata
}

一切准备就绪后，接下来就可以进行置位添加了。在添加前，先检测下集合是否已经包含了该元素。在添加完成后，还要记得要更新下 size。

实现代码如下：

if set.data[i]&posVal(n) == 0 {
	// 设置元素到集合中
	set.data[i] |= posVal(n)
	s.size++
}

好了！基础的方法就介绍这么多吧。

当然，这里的方法还可以增加更多，比如查找当前元素的下一个元素，将某个范围值都添加进集合等等等。

集合方法

介绍完了基础的方法，再继续介绍集合一些特有的方法，交并差。

computeSize

在正式介绍这些方法前，先引入一个辅助方法，用于计算集合中的元素个数。之所以要引入这个方法，是因为交并差没有办法像之前在增删的时候更新 size，要重新计算一下。

实现代码如下：

func (set *BitSet) computeSize() int {
	d := set.data
	n := 0
	for i, len := 0, len(d); i < len; i++ {
		if w := d[i]; w != 0 {
			n += bits.OnesCount64(w)
		}
	}

	return n
}

这是一个不可导出的方法，只能内部使用。遍历 data 的每个 uint64，如果非 0，则统计其中的元素个数。元素个数统计用到了标准库中的 bits.OnesCount64 方法。

方法定义

继续介绍集合的几个方法，它们的定义类似，都是一个 BitSet 与另一个 BitSet 的运算，如下：

// 交集
func (set *BitSet) Intersect(other *BitSet) *BitSet {
	// ...
}
// 并集
func (set *BitSet) Union(other *BitSet) *BitSet {
	// ...
}
// 差集
func (set *BitSet) Difference(other *BitSet) *BitSet {
	// ...
}

intersect

先介绍 Intersect，即计算交集的方法。

一个重要前提，因为交集是 与运算，结果肯定位于两个参与运算的那个小范围集合中，所以，开辟空间和遍历可以缩小到这个范围进行。

实现代码如下：

// 首先，获取这个小范围的集合的长度
minLen := min(len(set.data), len(other.data))

// 以 minLen 开辟空间
intersectSet := &BitSet{
	data: make([]uint64, minLen),
}

// 以 minLen 进行遍历计算交集
for i := minLen - 1; i >= 0; i-- {
	intersectSet.data[i] = set.data[i] & other.data[i]
}

intersectSet.size = set.computeSize()

这里通过遍历逐一对每个 uint64 执行 与运算 实现交集。在完成操作后，记得计算下 intersectSet 中元素个数，即 size 的值。

union

再介绍并集 Union 方法。

它的计算逻辑和 Intersect 相反。并集结果所占据的空间和以参与运算的两个集合的较大集合为准。

实现代码如下：

var maxSet, minSet *BitSet
if len(set.data) > len(other.data) {
	maxSet, minSet = set, other
} else {
	maxSet, minSet = other, set
}

unionSet := &BitSet{
	data: make([]uint64, len(maxSet.data)),
}

创建的 unionSet 中，data 分配空间是 len(maxSet.data)。

因为两个集合中的所有元素满足最终结果，但 maxSet 的高位部分无法通过遍历和 minSet 执行运算，直接拷贝进结果中即可。

minLen := len(minSet.data)
copy(unionSet.data[minLen:], maxSet.data[minLen:])

最后，遍历两个集合 data，通过 或运算 计算剩余的部分。

for i := 0; i < minLen; i++ {
	unionSet.data[i] = set.data[i] | other.data[i]
}

// 更新计算 size
unionSet.size = unionSet.computeSize()

difference

介绍最后一个与集合相关的方法，Difference，即差集操作。

差集计算结果 differenceSet 的分配空间由被减集合 set 决定。其他的操作和 Intersect 和 Union 类似，位运算通过 &^ 实现。

setLen := len(set.data)

differenceSet := &BitSet{
	data: make([]uint64, setLen),
}

如果 set 的长度大于 other，则需要先将无法进行差集运算的内容拷贝下。

minLen := setLen
if setLen > otherLen {
	copy(differenceSet.data[otherLen:], set.data[otherLen:])
	minLen = otherLen
}

记录下 minLen 用于接下来的位运算。

// 遍历 data 执行位运算。
for i := 0; i < minLen; i++ {
	differenceSet.data[i] = set.data[i] &^ other.data[i]
}

differenceSet.size = differenceSet.computeSize()

遍历集合的元素

单独说下集合元素的遍历，之前查看集合元素一直都是通过 Contains 方法检查是否存在。能不能把集合中的每个元素全部遍历出来呢？

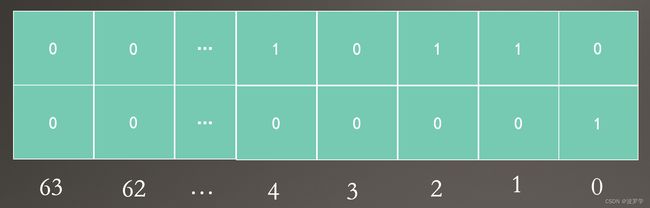
再看下 bitset 的结构，如下：

上面的集合中，第一行 int64 的第一个元素是 1，尾部有一位被置零。通过观察发现，前面有几个 0，第一个元素就是什么值。

第二行 int64 的第一元素尾部没有 0，那它的值就是 0 吗？当然不是，还有前面一行的 64 位基础，所以它的值是 64+0。

总结出什么规律了吗？笨，理论功底太差，满脑子明白，就是感觉写不清楚。看代码吧！

先看函数定义：

func (set *BitSet) Visit(do func(int) (skip bool)) (aborted bool) {
	//...
}

输入参数是一个回调函数，通过它获取元素的值，不然每次都要写一大串循环运算逻辑，不太可能。回调函数的返回值 bool，表明是否继续遍历。Visit 的返回值表明是函数是非正常结束的。

实现代码如下：

d := set.data
for i, len := 0, len(d); i < len; i++ {
	w := d[i]
	if w == 0 {
		continue
	}

	// 理论功力不好，不知道怎么描述了。哈哈
	// 这小段代码可以理解为从元素值到 index 的逆运算，
	// 只不过得到的值是诸如 0、64、128 的第一个位置的值。
	// 0 << 6，还是 0，1 << 6 就是 64，2 << 6 的就是 128
	n := i << shift
	for w != 0 {
		// 000.....000100 64~128 的话，表示 66，即 64 + 2，这个 2 可以由结尾 0 的个数确定
		// 那怎么获取结果 0 的个数呢？可以使用 bits.TrailingZeros64 函数
		b := bits.TrailingZeros64(w)
		if do(n + b) {
			return true
		}
		// 将已经检查的位清零
		// 为了保证尾部 0 的个数能代表元素的值
		w &^= 1 << uint64(b)
	}
}

使用也非常方便，示例代码如下：

set := NewBitSet(1, 2, 10, 99)
set.Visit(func(n int) bool {
	fmt.Println(n)
	return false
})

好了，就说这么多吧！

总结

本篇文章主要是参考了几个开源包的基础上，介绍了 bitset 的实现，比如 bit 和 bitset 等。

总的来说，位运算就是没有那么直观，感觉脑子不够用了。

博客地址：详细介绍 Go 中如何实现 bitset