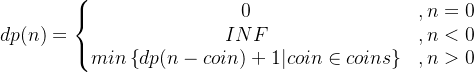找零钱问题（动态规划问题）【Java实现】

《labuladong的算法小抄》学习笔记

问题描述

给你一个整数数组 coins ，表示不同面额的硬币；以及一个整数 amount ，表示总金额。计算并返回可以凑成总金额所需的 最少的硬币个数 。如果没有任何一种硬币组合能组成总金额，返回 -1 。

你可以认为每种硬币的数量是无限的。

举例：

输入：coins=[1,2,5] amount=11;

输出：3

---

方法1：暴力递归

这是一个经典的动态规划问题，因为它具有”最佳子结构“。比如要求amount=11（原问题），那么可以先求amount=10（子问题），即子问题之间不具有相关性。

动态规划步骤

1. 确定base case：当amount=0时算法结束

2. 确定”状态“，也就是原问题和子问题中的变量，本题中是amount

3. 确定”选择“，也就是导致”状态“产生变化的行为。本题为选择硬币的面值

4. 明确dp函数/数组的定义：输入目标金额，返回凑出目标金额的最小硬币数量。

 代码实现

class Solution {
    /*找零钱问题：自顶向下解法*/

    public int coinChange(int[] coins, int amount) {
        return dp(coins, amount);
    }

    public int dp(int[] coins, int amount) { 
        //函数返回值是零钱个数
        if (amount == 0) return 0;
        else if(amount < 0) return -1;
        final int INF = 2147483645;  //定义一个无穷大的变量
        int res = INF;

        for (int i=0; i<=coins.length-1; i++) {  //暴力穷举法
            int coin = coins[i];
            int surproblem = dp(coins, (amount - coin)); 
            //从总数中减掉选中的钱，迭代输出零钱张数
            if (surproblem == -1) continue; //子问题无解，跳出循环
            res = Math.min(res, surproblem+1);
            //零钱张数+1，和已有的零钱数量相比较，选最小的
        }
        if (res == INF) res=-1; //若零钱张数仍为无穷，返回-1
        return res;
    }
}

 以上算法算是“暴力解法”，即列举出所有的情况，选出最小钱张数，状态转移方程为：

这样解虽然很直观，但其中有很多步骤是重叠的，总时间复杂度为o(kn^k)，有没有一种办法可以让算法不进行重复的运算呢。 

---

方法2：带“备忘录”的递归

方法2与方法1类似，仅添加了一个哈希表memo作为“备忘录”（Java中没有字典），存储已经运算过的值。 

使用哈希表（HashMap）的原因是因为存储不连续，且需要“一 一对应”，Key为总金额，Value为钱张数。代码如下

class Solution {

    public int coinChange(int[] coins, int amount) {
        HashMap memo = new HashMap<>(); 
        /*用哈希表作为备忘录（JAVA里面没有字典）
        key是金额，value是钱张数*/
        return dp(coins, amount, memo);
    }

    public int dp(int[] coins, int amount, HashMap memo) { 
        //函数返回值是零钱张数
        if (memo.get(amount) != null) return memo.get(amount);  //查表 
        if (amount == 0) return 0;
        else if(amount < 0) return -1;

        final int INF = 2147483645;  //定义一个无穷大的变量
        int res = INF;

        for (int i=0; i<=coins.length-1; i++) {  
            int coin = coins[i];
            int surproblem = dp(coins, (amount - coin), memo); 
            //从总数中减掉选中的钱，迭代输出零钱张数
            if (surproblem == -1) continue; //子问题无解，跳出循环
            res = Math.min(res, surproblem+1);
            //零钱张数+1，和已有的零钱数量相比较，选最小的
        }
        if (res == INF) res=-1; //若零钱张数仍为无穷，返回-1
        memo.put(amount, res);  //存进哈希表里
        return memo.get(amount);
    }
}

显然，“备忘录”法大大的减少了子问题的数目，消除了子问题的冗余，运算时间复杂度为o(kn)。

---

方法3：dp数组的迭代解法（自底向上）

自底向上的思想是从最小子问题出发，逐步增加“状态”，最终达到目标状态。

class Solution {
    public int coinChange(int[] coins, int amount) {
        HashMap memo = new HashMap<>();
        //此处是为了防止出现amount=0时下一步循环不能用的情况
        if (amount == 0) return 0;
        //自底向上方法，从0到amount依次计算，存储到memo
        for (int i=0; i<=amount; i++) {
            dp(coins, i, memo);
        }
        return memo.get(amount);
    }
    
    public int dp(int[] coins, int amount, HashMap memo) {
        if (memo.get(amount) != null) return memo.get(amount);
        if (amount == 0) return 0;
        else if (amount < 0) return -1;
        final int INF = 100000;
        int res = INF;
        
        for (int coin:coins) {
            int surproblem = dp(coins, (amount - coin), memo);
            if (surproblem == -1) continue;
            res = Math.min(res, surproblem + 1);
        }
        memo.put(amount, res);
        if (memo.get(amount) == INF) memo.put(amount, -1);
        return memo.get(amount);
    }
}