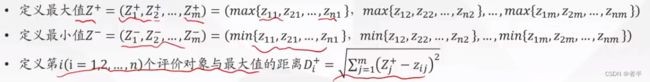TOPSIS（内含python完整代码)

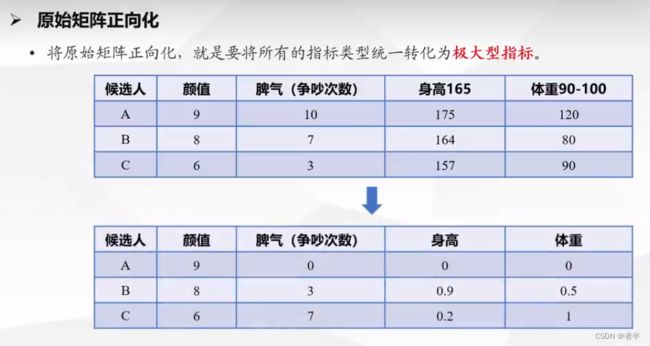
背景：依然是评价决策类问题

层次分析法的弊端：层次分析法决策层不能太多,而且构造判断矩阵相对了主观。

那有没有别的方法呢?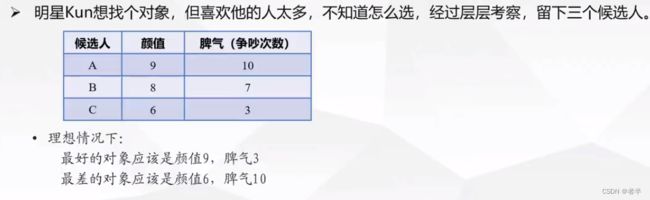
那怎么衡量A、B、C和最好、最差的距离呢?
把(9,3),(6,10)作为二维平面的一个点
距离最好点最近或者距离最差点最远的的就是综合条件最好的

也就是点越靠近左上角越差，越靠近矩阵右下角越好

这里(6,10)也就是反理想解，也就是最差的对象，(9,3)是理想解，也就是综合条件最好的对象。

具体概念：

TOPSIS法是一种理想目标相似性的顺序选优技术,在多目标决策分析中是一种非常有效的方法。
它通过归一化后(去量纲化)的数据规范化矩阵,找出多个目标中最优目标和最劣目标(分别用理想解化和反理想解表示),分别计算各评价目标与理想解和反理想想解的距离,获得各目标与理想解的贴近度,按理想解贴近度的大小排序,以此作为评价目标优劣的依损。贴近度取值在0~1之间,该值愈接近1,表示相应的评价目标越接近最优水平;反之,该值愈接近0,表示评价目标越接近最劣水平。

基本步骤：
 

标准化的目的是消除不同指标量纲的影响。

最大值和最小值都是列的（因为是各个指标），行是评价对象。相当于把每个指标的最大值取出组合成新向量，然后再利用距离公式算出每个候选人对象和最好对象各项指标之间的差距。

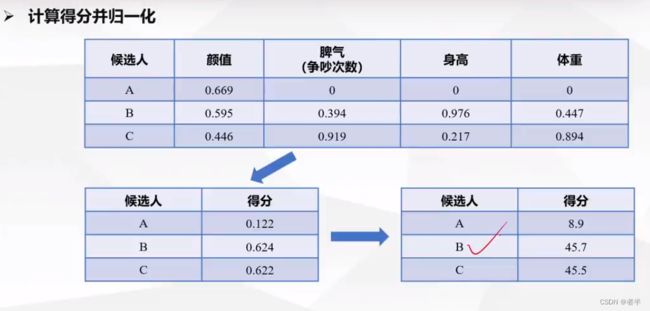
再利用下列公式进行求得分（未归一化的）

具体实现代码：

import numpy as np  # 导入numpy库，用于进行科学计算

# 从用户输入中接收参评数目和指标数目，并将输入的字符串转换为数值
print("请输入参评数目：")
n = eval(input())  # 接收参评数目
print("请输入指标数目：")
m = eval(input())  # 接收指标数目

# 接收用户输入的类型矩阵，该矩阵指示了每个指标的类型（极大型、极小型等）
print("请输入类型矩阵：1:极大型，2：极小型，3：中间型，4：区间型")
kind = input().split(" ")  # 将输入的字符串按空格分割，形成列表

# 接收用户输入的矩阵并转换为numpy数组
print("请输入矩阵：")
A = np.zeros(shape=(n, m))  # 初始化一个n行m列的全零矩阵A
for i in range(n):
    A[i] = input().split(" ")  # 接收每行输入的数据
    A[i] = list(map(float, A[i]))  # 将接收到的字符串列表转换为浮点数列表
print("输入矩阵为：\n{}".format(A))  # 打印输入的矩阵A

# 极小型指标转化为极大型指标的函数
def minTomax(maxx, x):
    x = list(x)  # 将输入的指标数据转换为列表
    ans = [[(maxx-e)] for e in x]  # 计算最大值与每个指标值的差，并将其放入新列表中
    return np.array(ans)  # 将列表转换为numpy数组并返回

# 中间型指标转化为极大型指标的函数
def midTomax(bestx, x):
    x = list(x)  # 将输入的指标数据转换为列表
    h = [abs(e-bestx) for e in x]  # 计算每个指标值与最优值之间的绝对差
    M = max(h)  # 找到最大的差值
    if M == 0:
        M = 1  # 防止最大差值为0的情况
    ans = [[(1-e/M)] for e in h]  # 计算每个差值占最大差值的比例，并从1中减去，得到新指标值
    return np.array(ans)  # 返回处理后的numpy数组

# 区间型指标转化为极大型指标的函数
def regTomax(lowx, highx, x):
    x = list(x)  # 将输入的指标数据转换为列表
    M = max(lowx-min(x), max(x)-highx)  # 计算指标值超出区间的最大距离
    if M == 0:
        M = 1  # 防止最大距离为0的情况
    ans = []
    for i in range(len(x)):
        if x[i]highx:
            ans.append([(1-(x[i]-highx)/M)])  # 如果指标值大于上限，则计算其与上限的距离比例
        else:
            ans.append([1])  # 如果指标值在区间内，则直接取为1
    return np.array(ans)  # 返回处理后的numpy数组

# 统一指标类型，将所有指标转化为极大型指标
X = np.zeros(shape=(n, 1))
for i in range(m):
    if kind[i]=="1":  # 如果当前指标为极大型，则直接使用原值
        v = np.array(A[:, i])
    elif kind[i]=="2":  # 如果当前指标为极小型，调用minTomax函数转换
        maxA = max(A[:, i])
        v = minTomax(maxA, A[:, i])
    elif kind[i]=="3":  # 如果当前指标为中间型，调用midTomax函数转换
        print("类型三：请输入最优值：")
        bestA = eval(input())
        v = midTomax(bestA, A[:, i])
    elif kind[i]=="4":  # 如果当前指标为区间型，调用regTomax函数转换
        print("类型四：请输入区间[a, b]值a：")
        lowA = eval(input())
        print("类型四：请输入区间[a, b]值b：")
        highA = eval(input())
        v = regTomax(lowA, highA, A[:, i])
    if i==0:
        X = v.reshape(-1, 1)  # 如果是第一个指标，直接替换X数组
    else:
        X = np.hstack([X, v.reshape(-1, 1)])  # 如果不是第一个指标，则将新指标列拼接到X数组上
print("统一指标后矩阵为：\n{}".format(X))  # 打印处理后的矩阵X

# 对统一指标后的矩阵X进行标准化处理
X = X.astype('float')  # 确保X矩阵的数据类型为浮点数
for j in range(m):
    X[:, j] = X[:, j]/np.sqrt(sum(X[:, j]**2))  # 对每一列数据进行归一化处理，即除以该列的欧几里得范数
print("标准化矩阵为：\n{}".format(X))  # 打印标准化后的矩阵X

# 最大值最小值距离的计算
x_max = np.max(X, axis=0)  # 计算标准化矩阵每列的最大值
x_min = np.min(X, axis=0)  # 计算标准化矩阵每列的最小值
d_z = np.sqrt(np.sum(np.square((X - np.tile(x_max, (n, 1)))), axis=1))  # 计算每个参评对象与最优情况的距离d+
d_f = np.sqrt(np.sum(np.square((X - np.tile(x_min, (n, 1)))), axis=1))  # 计算每个参评对象与最劣情况的距离d-
print('每个指标的最大值:', x_max)
print('每个指标的最小值:', x_min)
print('d+向量:', d_z)
print('d-向量:', d_f)

# 计算每个参评对象的得分排名
s = d_f/(d_z+d_f)  # 根据d+和d-计算得分s，其中s接近于1则表示较优，接近于0则表示较劣
Score = 100*s/sum(s)  # 将得分s转换为百分制，便于比较
for i in range(len(Score)):
    print(f"第{i+1}个标准化后百分制得分为：{Score[i]}")  # 打印每个参评对象的得分

---

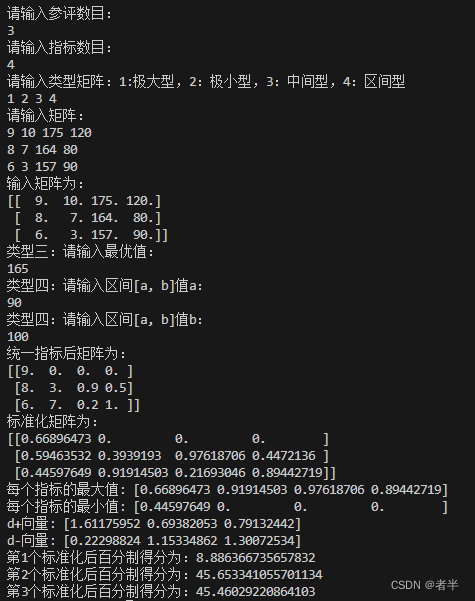
输入输出如下图所示：

推荐网课：数模加油站，该博客均为作者本人学习笔记，仅供参考，如有错误，请及时指出。