代码随想录 - 数组

总结概述 

数组理论基础

数组是存放在连续内存空间上的相同类型数据的集合。如图所示：

注意：

• 数组下标都是从0开始的。
• 数组内存空间的地址是连续的

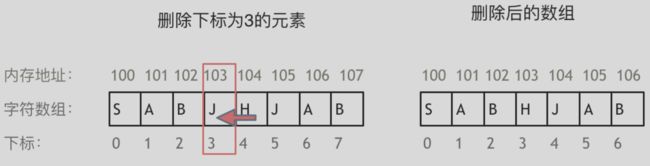
       数组的在内存空间的地址是连续的，所以在删除或者增添元素的时候，就难免要移动其他元素的地址。

例如删除下标为3的元素，需要对下标为3的元素后面的所有元素都要做移动操作，如图所示：

如果使用C++的话，要注意vector 和 array的区别，vector的底层实现是array，严格来讲vector是容器，不是数组。

数组的元素是不能删的，只能覆盖。

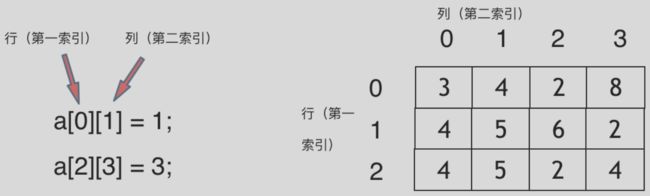
二维数组直接上图

以C++为例，在C++中二维数组是连续分布的。

我们来做一个实验，C++测试代码如下：

void test_arr() {
    int array[2][3] = {
		{0, 1, 2},
		{3, 4, 5}
    };
    cout << &array[0][0] << " " << &array[0][1] << " " << &array[0][2] << endl;
    cout << &array[1][0] << " " << &array[1][1] << " " << &array[1][2] << endl;
}

int main() {
    test_arr();
}

 测试地址为：

000000CD9F13F968 000000CD9F13F96C 000000CD9F13F970
000000CD9F13F974 000000CD9F13F978 000000CD9F13F97C

各地址差一个4，就是4个字节，因这是一个int型的数组，所以两个相邻数组元素地址差4个字节。 

注意地址为16进制，可以看出二维数组地址是连续一条线的。

所以可以看出在C++中二维数组在地址空间上是连续的。

---

二分查找

704. 二分查找

给定一个 n 个元素有序的（升序）整型数组 nums 和一个目标值 target  ，写一个函数搜索 nums 中的 target，如果目标值存在返回下标，否则返回 -1。

解题思路 

二分法的思想很简单，因为整个数组是有序的，数组默认是递增的。

• 首先选择数组中间的数字和需要查找的目标值比较
• 如果相等最好，就可以直接返回答案了
• 如果不相等
  • 如果中间的数字大于目标值，则中间数字向右的所有数字都大于目标值，全部排除
  • 如果中间的数字小于目标值，则中间数字向左的所有数字都小于目标值，全部排除

二分法就是按照这种方式进行快速排除查找的。【二分查找】详细图解

这道题目的前提是数组为有序数组，同时题目还强调数组中无重复元素，因为一旦有重复元素，使用二分查找法返回的元素下标可能不是唯一的，这些都是使用二分法的前提条件，当大家看到题目描述满足如上条件的时候，可要想一想是不是可以用二分法了。

二分法主要就是对区间的定义理解清楚，在循环中始终坚持根据查找区间的定义来做边界处理。所以循环条件和赋值问题必须统一，也就是循环不变量。

区间的定义就是不变量，在循环中坚持根据查找区间的定义来做边界处理，就是循环不变量规则。

写二分法，区间的定义一般为两种，左闭右闭即[left, right]，或者左闭右开即[left, right)。 

二分法最重要的两个点：就是循环条件和后续的区间赋值问题

• while循环中 left 和 right 的关系，到底是 left <= right 还是 left < right
• 迭代过程中 middle 和 right 的关系，到底是 right = middle - 1 还是 right = middle

解题代码

class Solution {
public:
    int search(vector& nums, int target) {
        int left = 0;
        int right = nums.size(); // 定义target在左闭右开的区间里，即：[left, right)
        while (left < right) { // 因为left == right的时候，在[left, right)是无效的空间，所以使用 <
            int middle = left + ((right - left) >> 1); // 防止溢出 等同于(left + right)/2
            if (nums[middle] > target) {
                right = middle; // target 在左区间，在[left, middle)中
            } else if (nums[middle] < target) {
                left = middle + 1; // target 在右区间，在[middle + 1, right)中
            } else { // nums[middle] == target
                return middle; // 数组中找到目标值，直接返回下标
            }
        }
        // 未找到目标值
        return -1;
    }
};

• 时间复杂度：O(log n)
• 空间复杂度：O(1)

35. 搜索插入位置https://leetcode.cn/problems/search-insert-position/34. 在排序数组中查找元素的第一个和最后一个位置https://leetcode.cn/problems/find-first-and-last-position-of-element-in-sorted-array/

 27. 移除元素

解题思路 

数组的元素在内存地址中是连续的，不能单独删除数组中的某个元素，只能覆盖。

双指针法：双指针算法

通过一个快指针和慢指针在一个for循环下完成两个for循环的工作。 

• 对撞指针：左右两个指针，向中间靠拢；
• 快慢指针：左右两个指针，一块一慢；
• 滑动窗口：左右两个指针组成一个"窗口"，右指针不断扩张，左指针按条件收缩。

三个关键点：

• 指针的起始位置的选取
• 指针的移动方向
• 指针的移动速度

 解题代码

// 时间复杂度：O(n)
// 空间复杂度：O(1)
class Solution {
public:
    int removeElement(vector& nums, int val) {
        int slowIndex = 0;
        for (int fastIndex = 0; fastIndex < nums.size(); fastIndex++) {
            if (val != nums[fastIndex]) {
                nums[slowIndex++] = nums[fastIndex]; // 将数组从右到左地复制
            }
        }
        return slowIndex;
    }
};

977.有序数组的平方

解题思路

解题代码

class Solution {
public:

    vector sortedSquares(vector& nums) {
        vector Res(nums.size(),0);
        int k = nums.size()-1;

        //两个指针++和--是有条件的，故不写在for循环里面
        for(int leftIndex = 0, rightIndex = nums.size()-1; leftIndex <= rightIndex;  ){ 
            if((nums[leftIndex]*nums[leftIndex]) > (nums[rightIndex]*nums[rightIndex])){
                Res[k--] = nums[leftIndex]*nums[leftIndex];
                leftIndex++;
            }
            else{
                Res[k--] = nums[rightIndex]*nums[rightIndex];
                rightIndex--;
            }
        }
        return Res;
    }
};

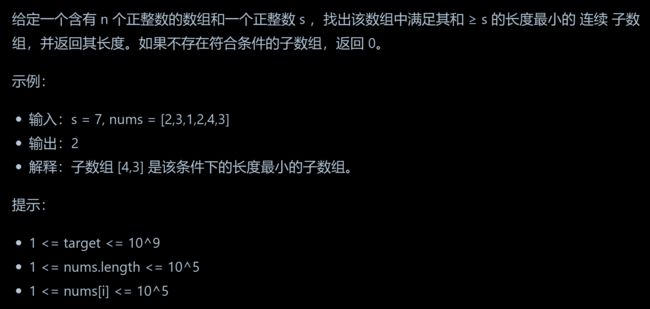
 209. 长度最小的子数组

 解题思路

可以发现滑动窗口的精妙之处在于根据当前子序列和大小的情况，不断调节子序列的起始位置。

解题代码

/* 时间复杂度：O(n)   空间复杂度：O(1) */
class Solution {
public:
    int minSubArrayLen(int target, vector& nums) {
        int head = 0; // 滑动窗口数值之和
        int sum = 0;  // 滑动窗口数值之和
        int subLen = 0;  // 滑动窗口的长度
        int res = nums.size()+1; // 定义最大长度

        for(int tail = 0; tail < nums.size(); tail++){
            sum += nums[tail];

            // 注意这里使用while，每次更新head（起始位置），并不断比较子序列是否符合条件
            while(sum >= target){
                subLen = (tail - head + 1);  // 取子序列的长度
                res = res < subLen ? res : subLen;
                sum -= nums[head++];  // 这里体现出滑动窗口的精髓之处，不断变更head（子序列的起始位置）
            }
        }
        // 如果res没有被赋值的话，就返回0，说明没有符合条件的子序列
        return res == (nums.size()+1) ? 0 : res;
    }
};

 76. 最小覆盖子串   哈希表维护滑动窗口

滑动窗口总结 

滑动窗口的理解

       滑动窗口也可以理解为双指针法的一种！只不过这种解法更像是一个窗口的移动，所以叫做滑动窗口更适合一些。

      可以用以解决数组/字符串的子元素相关问题，并且可以将嵌套的循环问题，转换为单循环问题，从而降低时间复杂度。故滑动窗口算法的复杂度一般为 O(n)。

主要确定如下三点：

• 窗口内是什么？
• 如何移动窗口的起始位置？
• 如何移动窗口的结束位置？

模板 

1、声明左右两个指针left和right，初始时都指向起始位置 left = right = 0。
2、满足不了条件是（while 窗口内不符合维护的条件），
   right 指针不停地后移以扩大窗口 [left, right]接近目标，
   直到窗口中的序列符合要求。
3、找到一个符合要求的子序列时，停止移动 right的值，
   转而不断移动左端 left 指针以缩小窗口 [left, right]，
   直到窗口中的序列不再符合要求。同时，每次增加 left前，都要更新一轮结果。
4、重复第 2 和第 3 步，直到 right 到达序列的尽头。

1寻找最长：
如果窗口满足条件，R向右滑动扩大窗口，更新最优值；
如果窗口不满足条件，L向右缩小窗口。
2寻找最短：
如果窗口满足条件，L向右滑动扩大窗口，更新最优值；
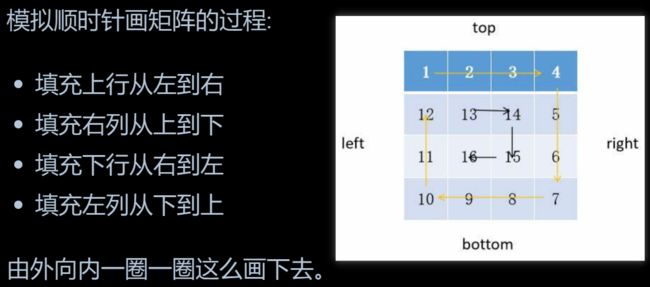
如果窗口不满足条件，R向右缩小窗口。

59. 螺旋矩阵 II

解题思路

跑一段直线到头削掉一层（按照固定规则，不断更新边界）

填充步骤： 在每一轮循环中：

• 从左到右填充当前层的上边界；    更新上边界，向内移动一行。
• 从上到下填充当前层的右边界；    更新右边界，向内移动一列。
• 从右到左填充当前层的下边界；    更新下边界，向内移动一行。
• 从下到上填充当前层的左边界；    更新左边界，向内移动一列。

循环直到填满整个矩阵。

解题代码

        代码通过在每一轮循环中按照顶、右、底、左的顺序填充数字，不断缩小螺旋层的边界，最终填满整个矩阵。 

class Solution {
public:
    vector> generateMatrix(int n) {
        int t = 0;      // 初始化螺旋层的上边界
        int b = n-1;    // 初始化螺旋层的下边界
        int l = 0;      // 初始化螺旋层的左边界
        int r = n-1;    // 初始化螺旋层的右边界
        vector> ans(n, vector(n)); // 创建一个 n x n 的矩阵，所有元素初始化为 0
        int k = 1; // 用于表示要填充的数字，从 1 开始

        // 开始填充数字，直到填满整个矩阵
        while(k <= n*n){
            // 从左到右填充当前螺旋层的上边界
            for(int i=l; i<=r; ++i, ++k) 
                ans[t][i] = k;

            ++t; // 上边界向内移动一行，因为上边界行已经填充完毕

            // 从上到下填充当前螺旋层的右边界
            for(int i=t; i<=b; ++i, ++k) 
                ans[i][r] = k;

            --r; // 右边界向内移动一列，因为右边界列已经填充完毕

            // 从右到左填充当前螺旋层的下边界
            for(int i=r; i>=l; --i, ++k) 
                ans[b][i] = k;

            --b; // 下边界向内移动一行，因为下边界行已经填充完毕

            // 从下到上填充当前螺旋层的左边界
            for(int i=b; i>=t; --i, ++k) 
                ans[i][l] = k;

            ++l; // 左边界向内移动一列，因为左边界列已经填充完毕
        }

        return ans; // 返回填充完毕的矩阵
    }
};

54. 螺旋矩阵 代码如下：

class Solution {
public:
    vector spiralOrder(vector>& matrix) {
        if (matrix.empty() || matrix[0].empty()) {
            return {}; // 如果输入的矩阵是空的，直接返回一个空数组
        }

        int rows = matrix.size(), columns = matrix[0].size();
        int total = rows * columns;
        vector ans(total); // 创建一个数组来存放螺旋顺序的元素

        int left = 0, right = columns - 1, top = 0, bottom = rows - 1;
        int index = 0; // 用于在 ans 数组中定位当前要填充的位置

        while (index < total) {
            // 从左到右填充上边界元素，并将当前元素填充到 ans 数组中
            for (int i = left; i <= right && index < total; ++i) {
                ans[index++] = matrix[top][i]; 
            }
            ++top; // 上边界向内移动一行

            // 从上到下填充右边界元素，并将当前元素填充到 ans 数组中
            for (int i = top; i <= bottom && index < total; ++i) {
                ans[index++] = matrix[i][right]; 
            }
            --right; // 右边界向内移动一列

            // 从右到左填充下边界元素，并将当前元素填充到 ans 数组中
            for (int i = right; i >= left && index < total; --i) {
                ans[index++] = matrix[bottom][i]; 
            }
            --bottom; // 下边界向内移动一行

            // 从下到上填充左边界元素，并将当前元素填充到 ans 数组中
            for (int i = bottom; i >= top && index < total; --i) {
                ans[index++] = matrix[i][left]; 
            }
            ++left; // 左边界向内移动一列
        }
        return ans; // 返回填充好的一维数组
    }
};